Workshop 08: Reaction mechanisms and catalysis

Lecture notes for chemical reaction engineering

Try following problems from Fogler 5e (Fogler (2016))

We will go through some of these problems in the workshop.

P 9-4, P 9-5, P 9-6, P 10-3, P 10-14, P 10-19

P 9-4

The pyrolysis of acetaldehyde is believed to take place according to the following sequence:

\ce{ CH3CHO ->[ k1 ] CH3* + CHO* }

\ce{ CH3* + CH3CHO ->[ k2 ] CH3* + CO + CH4 }

\ce{ CHO* + CH3CHO ->[ k3 ] CH3* + 2 CO + H2 }

\ce{ 2 CH3* ->[ k4 ] C2H6 }

1. Derive the rate expression for the rate of disappearance of acetaldehyde, r_{Ac}.

2. Under what conditions does it reduce to the equation at the beginning of Section 9.1 on page 334? (-r_{CH_3CHO} = k C_{CH_3CHO}^{3/2})

3. Sketch a reaction pathway diagram for this reaction.

Solution

Hand written solution

P 9-5

For each of the reactions in parts (a), (b), and (c), suggest a mechanism and apply the PSSH to learn if the mechanism is consistent with the rate law.

1. The gas-phase homogeneous oxidation of nitrogen monoxide (\ce{NO}) to dioxide (\ce{NO2})

   \ce{ 2 NO + O2 ->[ k ] 2 NO2 }

   is known to have a form of third-order kinetics, which suggests that the reaction is elementary as written, at least for low partial pressures of the nitrogen oxides. However, the rate constant k actually decreases with increasing absolute temperature, indicating an apparently negative activation energy. Because the activation energy of any elementary reaction must be positive, some explanation is in order.

   Provide an explanation, starting from the fact that an active intermediate species, NO 3 , is a participant in some other known reactions that involve oxides of nitrogen. Draw the reaction pathway.

2. The rate law for formation of phosgene, \ce{COCl2}, from chlorine, \ce{Cl2}, and carbon monoxide, \ce{CO}, has the rate law

   r_{COCl_2} = k C_{CO} C_{Cl_2}^{3/2}

   Suggest a mechanism for this reaction that is consistent with this rate law and draw the reaction pathway. Hint: Cl formed from the dissociation of \ce{Cl2} is one of the two active intermediates.

3. Suggest an active intermediate(s) and mechanism for the reaction \ce{ H2 + Br2 -> 2 HBr }. Use the PSSH to show whether or not your mechanism is consistent with the rate law

   r_{HBr} = \frac{k C_{H_2} C_{Br}^{3/2}}{C_{HBr} + k_2 C_{Br_2}}

Solution

Hand written solution problem 9-5 b

Hand written solution problem 9-5 c

P 9-6

(Tribology) Why you change your motor oil? One of the major reasons for engine-oil degradation is the oxidation of the motor oil. To retard the degradation process, most oils contain an antioxidant [see Ind. Eng. Chem. 26, 902 (1987)]. Without an inhibitor to oxidation present, the suggested mechanism at low temperatures is

\ce{ I2 ->[ k0 ] 2 I. }

\ce{ I. + RH ->[ k_i ] R. + HI }

\ce{ R. + O2 ->[ k_{p1} ] RO2. }

\ce{ RO2. + RH ->[ k_{p2} ] ROOH + R. }

\ce{ 2 RO2. ->[ k_t ] inactive }

where \ce{I2} is an initiator and RH is the hydrocarbon in the oil.

When an antioxidant is added to retard degradation at low temperatures, the following additional termination steps occur:

\ce{ RO2. + AH ->[ k_{A1} ] ROOH + A. }

\ce{ A. + RO2. ->[ k_{A2} ] inactive }

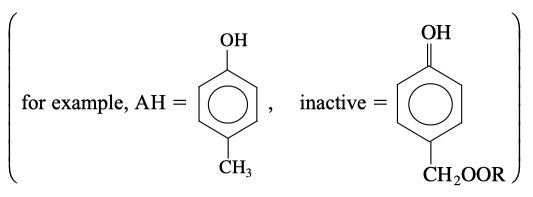
1. Derive a rate law for the degradation of the motor oil in the absence of an antioxidant at low temperatures.

2. Derive a rate law for the rate of degradation of the motor oil in the presence of an antioxidant for low temperatures.

3. How would your answer to part (a) change if the radicals \ce{I.} were produced at a constant rate in the engine and then found their way into the oil?

4. Sketch a reaction pathway diagram for both high and low temperatures, with and without antioxidant.

Solution

Hand written solution

P 10-3

t-Butyl alcohol (TBA) is an important octane enhancer that is used to replace lead additives in gasoline [Ind. Eng. Chem. Res., 27, 2224 (1988)]. TBA was produced by the liquid-phase hydration (W) of isobutene (I) over an Amberlyst-15 catalyst. The system is normally a multiphase mixture of hydrocarbon, water, and solid catalysts. However, the use of cosolvents or excess TBA can achieve reasonable miscibility.

The reaction mechanism is believed to be

\ce{ I + S <=> I.S }

\ce{ W + S <=> W.S }

\ce{ W.S + I.S <=> TBA.S + S }

\ce{ TBA.S <=> TBA + S }

Derive a rate law assuming:

1. The surface reaction is rate-limiting.

2. The adsorption of isobutene is limiting.

3. The reaction follows Eley–Rideal kinetics

   \ce{ I.S + W -> TBA.S }

   and the surface reaction is limiting.

4. Isobutene (I) and water (W) are adsorbed on different sites.

   \ce{ I + S1 <=> I.S1 }

   \ce{W + S2 <=> W.S2 }

   TBA is not on the surface, and the surface reaction is rate-limiting.

5. What generalization can you make by comparing the rate laws derived in parts (a) through (d)?

Solution

Hand written solution

P 10-14

Vanadium oxides are of interest for various sensor applications, owing to the sharp metal–insulator transitions they undergo as a function of temperature, pressure, or stress. Vanadium triisopropoxide (VTIPO) was used to grow vanadium oxide films by chemical vapor deposition [J. Electrochem. Soc., 136, 897 (1989)]. The deposition rate as a function of VTIPO pressure for two different temperatures follows.

T = 120 ^{\circ}C:

Growth Rate (\mum/h)	0.004	0.015	0.025	0.04	0.068	0.08	0.095	0.1
VTIPO Pressure (torr)	0.1	0.2	0.3	0.5	0.8	1.0	1.5	2.0

T = 200 ^{\circ}C:

Growth Rate (\mum/h)	0.028	0.45	1.8	2.8	7.2
VTIPO Pressure (torr)	0.05	0.2	0.4	0.5	0.8

In light of the material presented in this chapter, analyze the data and describe your results. Specify where additional data should be taken.

Solution

Hand written solution

P 10-19

With the increasing demand for xylene in the petrochemical industry, the production of xylene from toluene disproportionation has gained attention in recent years [Ind. Eng. Chem. Res., 26, 1854 (1987)]. This reaction,

\ce { 2 Toluene -> Benzene + Xylene }

\ce { 2 T -> B + X }

was studied over a hydrogen mordenite catalyst that decays with time. As a first approximation, assume that the catalyst follows second-order decay

r_d = k_d a^2

and the rate law for low conversions is

-r_T' = k_T P_T a

with k_T = 20 g \, mol/h \cdot kg-cat \cdot atm and k_d = 1.6 h^{-1} at 735 K.

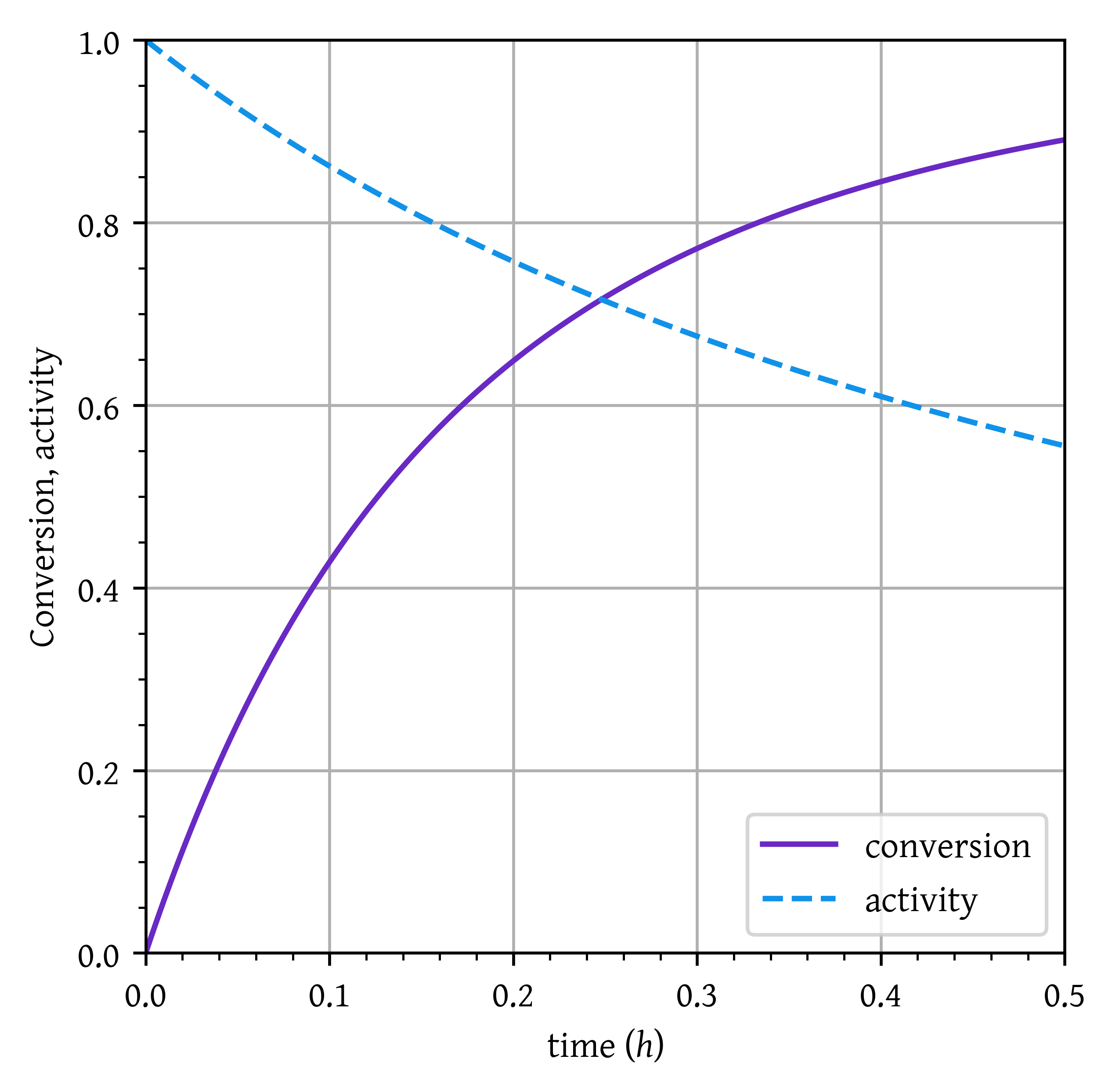
1. Compare the conversion-time curves in a batch reactor containing 5 kg-cat at different initial partial pressures (1 atm, 10 atm, etc.). The reaction volume containing pure toluene initially is 1 dm^3 and the temperature is 735 K.

2. What conversion can be achieved in a moving-bed reactor containing 50 kg of catalyst with a catalyst feed rate of 2 kg/h? Toluene is fed at a pressure of 2 atm and a rate of 10 mol/min.

3. Explore the effect of catalyst feed rate on conversion.

4. Suppose that E_T = 25 kcal/mol and E_d =10 kcal/mol. What would the temperature–time trajectory look like for a CSTR? What if E_T =10 kcal/mol and E_d =25 kcal/mol?

5. The decay law more closely follows the equation

   r_d = k_d P^2_T a^2

   with k_d =0.2 atm^{-2} h^{-1}. Redo parts (b) and (c) for these conditions.

Solution

Hand written solution

import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import solve_ivp

# constants

R = 8.314  # J/ (mol K)
RCAL = 1.987  # cal⋅/ mol K
RATM = 0.082  # atm dm^3/ (mol K)

# reaction
# 2 T -> B + X

# Components
# 0: Toluene
# 1: Benzene
# 2: Xylene

# Heats of formation at 298 K in J/mol
HF = np.array([50.1e3, 82.9e3, 17.4e3])

# Specific Heat Capacities J/mol K
CP = np.array([134, 136, 140])

# Stoichiometry
NU = np.array([-2, 0, 0])  # Reaction : 2T -> B + X

# Heat of reaction at reference temperature J/mol
DELTA_HR_TR = np.dot(NU, HF)

KT = 20  # g mol/h kg-cat atm  at 735K
KD = 1.6  # 1/h at 735K
ET = 25e3  # cal/mol
ED = 10e3  # cal/mol
TR = 735  # K reference temperature for KT and KD

# Functions
kt = lambda t: KT * np.exp((ET / RCAL) * ((1 / TR) - (1 / t)))
kd = lambda t: KD * np.exp((ED / RCAL) * ((1 / TR) - (1 / t)))

# rates
rd = lambda t, a: kd(t) * a**2
rt = lambda t, a, pt: a * kt(t) * pt  # this is -r_t


def batch_reactor(t, y, *args):

    # convert dependent variables
    x, a = y
    (w, pt0, nt0, T0) = args

    pt = pt0 * (1 - x)  # as delta = 0 (epsilon = 0)

    rate = rt(T0, a, pt)

    dxdt = rate * w / nt0
    dadt = -rd(T0, a)

    dydw = [dxdt, dadt]
    return dydw


# Problem data

# pressure and temperature
T0 = 735  # K
pt0 = 1  # atm
v = 1  # dm^3
w = 5  # kg
nt0 = 1e3 * pt0 * v / (RATM * T0)  # g mol

# Differential equations
# 0: dX/dt
# 1: da/dt

initial_conditions = np.array([0, 1])
args = (w, pt0, nt0, T0)

t_final = 0.5

sol = solve_ivp(
    batch_reactor,
    [0, t_final],
    initial_conditions,
    args=args,
    method="LSODA",
    dense_output=True,
)

# Extract solution
time = np.linspace(0, t_final, 1000)

# conversion
x = sol.sol(time)[0]

# activity
a = sol.sol(time)[1]

plt.plot(time, x, label="conversion")
plt.plot(time, a, label="activity")

plt.xlim(time[0], time[-1])
plt.ylim(0, 1)
plt.grid()
plt.legend()

plt.xlabel("time ($h$)")
plt.ylabel("Conversion, activity")

plt.show()

Figure 1: Conversion and activity

References

Fogler, H. Scott. 2016. Elements of Chemical Reaction Engineering. Fifth edition. Boston: Prentice Hall.