Workshop 03: Rate law and stoichiometry

Lecture notes for chemical reaction engineering

Solutions

Solutions to these problems are uploaded at Workshop 3 solutions

Try following problems from Fogler 5e(Fogler 2016).

P3-5, P3-10, P3-11, P3-12, P 4-6, P 4-8, P 4-11

We will go through some of these problems in the workshop.

P 3.12

Write the rate law for the following reactions assuming each reaction follows an elementary rate law. Give the units of k_A for each, keeping in mind some are homogeneous and some reactants are heterogeneous.

1. \ce{C2H6 -> C2H4 H2}

2. \ce{C2H4 + 1/2 O2 -> C2H4O}

3. \ce{(CH3)3COOC(CH3)3 <=> C2H6 + 2CH3COCH3}

4. \ce{nC4H10 <=> iC4H10}

5. \ce{ CH3COOC2H5 + C4H9OH <=> CH3COOC4H9 + C2H5OH}

6. \ce{2CH3NH2 <=>[][{cat}] (CH3)2NH + NH3}

7. \ce{ (CH3CO)2O + H2O <=> 2CH3COOH }

P3-10

The initial reaction rate for the elementary reaction \ce{2A + B -> 4C} was measured as a function of temperature when the concentration of A was 2 M and that of B was 1.5 M.

–r_A (mol/dm^3 s)	T(K)
0.002	300
0.046	320
0.72	340
8.33	360

1. What is the activation energy?

2. What is the frequency factor?

3. What is the rate constant as a function of temperature using Equation 1 and T_0 = 27 °C as the base case?

   k(T) = k(T_0) exp \left[ \frac{E}{R} \left( \frac{1}{T_0} - \frac{1}{T} \right)\right] \tag{1}

P 4-8

The gas-phase reaction

\ce{1/2 N2 + 3/2 H2 -> NH3}

is to be carried out isothermally first in a flow reactor. The molar feed is 50% \ce{H2} and 50% \ce{N2} , at a pressure of 16.4 atm and at a temperature of 227 \ ^{\circ}C?.

1. Construct a complete stoichiometric table.

2. Express the concentrations in mol/dm^3 of each for the reacting species as a function of conversion. Evaluate C_{A0}, \delta and \epsilon, and then calculate the concentrations of ammonia and hydrogen when the conversion of \ce{H2} is 60%.

3. Suppose by chance the reaction is elementary with k_{N_2} = 40 \ dm^3 /mol/s. Write the rate of reaction solely as a function of conversion for

   1. a flow reactor, and for

   2. a constant-volume batch reactor.

P 4-11

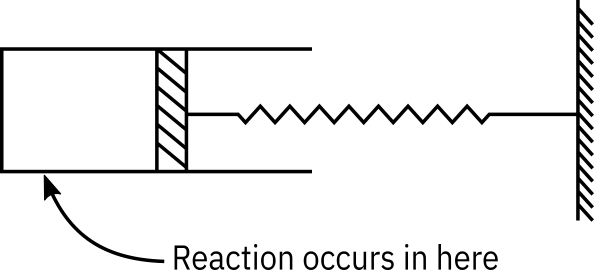
Consider a cylindrical batch reactor that has one end fitted with a frictionless piston attached to a spring (See Figure Figure 1). The reaction

\ce{A + B -> 8 C}

with the rate law

-r_A = k_1 C_A^2 C_B

is taking place in this type of reactor.

Figure 1: Cylindrical batch reactor

1. Write the rate law solely as a function of conversion, numerically evaluating all possible symbols.

2. What is the conversion and rate of reaction when V=0.2 \ ft^3 ?

Additional information:

Equal moles of A and B are present at t_0

Initial volume: 0.15 \ ft^3

Value of k_1 : 1.0 \ (ft^3 /lb mol)^2 \cdot s^{-1}

The spring constant is such that the relationship between the volume of the reactor and pressure within the reactor is

V = (0.1)\ (P) (V in ft^3 , P in atm)

Temperature of system (considered constant): 140 \ ^{\circ}F

Gas constant: 0.73 \ ft^3 atm/lb mol \cdot ^{\circ}R

References

Fogler, H. Scott. 2016. Elements of Chemical Reaction Engineering. Fifth edition. Boston: Prentice Hall.