Workshop 11: Distribution of residence time

Lecture notes for chemical reaction engineering

Solutions

Solutions to these problems are uploaded at Workshop 11 solutions

Try following problems from Fogler 5e (Fogler (2016)) P 16-3, P 16-6, P 16-11

We will go through some of these problems in the workshop.

P 16-3

Consider the E(t) curve below.

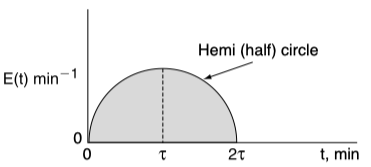
Mathematically this hemi circle is described by these equations:

For 2\tau >= t >= 0, then E(t) = \sqrt{\tau^2 - (t - \tau)^2} min^–1 (hemi circle)

For t > 2\tau, then E(t) = 0

1. What is the mean residence time?

2. What is the variance?

P 16-6

An RTD experiment was carried out in a nonideal reactor that gave the following results:

E(t) = 0	for	t < 1 \, min
E(t) = 1.0 \, min^{-1}	for	1 <= t <= 2 \, min
E(t) = 0	for	t > 2 \, min

1. What are the mean residence time, t_m, and variance \sigma^2?

2. What is the fraction of the fluid that spends a time 1.5 minutes or longer in the reactor?

3. What fraction of fluid spends 2 minutes or less in the reactor?

4. What fraction of fluid spends between 1.5 and 2 minutes in the reactor?

P 16-11

The volumetric flow rate through a reactor is 10 dm³/min. A pulse test gave the following concentration measurements at the outlet:

t (min)	c \times 10^5	t (min)	c \times 10^5
0	0	15	238
0.4	329	20	136
1.0	622	25	77
2	812	30	44
3	831	35	25
4	785	40	14
5	720	45	8
6	650	50	5
8	523	60	1
10	418

1. Plot the external-age distribution E(t) as a function of time.

2. Plot the external-age cumulative distribution F(t) as a function of time.

3. What are the mean residence time t_m and the variance, \sigma^2 ?

4. What fraction of the material spends between 2 and 4 minutes in the reactor?

5. What fraction of the material spends longer than 6 minutes in the reactor?

6. What fraction of the material spends less than 3 minutes in the reactor?

7. Plot the normalized distributions E(\Phi) and F(\Phi) as a function of (\Phi).

8. What is the reactor volume?

9. Plot the internal-age distribution I(t) as a function of time.

10. What is the mean internal age \alpha_m ?

References

Fogler, H. Scott. 2016. Elements of Chemical Reaction Engineering. Fifth edition. Boston: Prentice Hall.