Workshop 07: Non-isothermal reactor design
Lecture notes for chemical reaction engineering
Solutions to these problems are uploaded at Workshop 7 solutions
Try following problems from Fogler 5e P 11-5, P 11-6, P 12-6, P 12-21
We will go through some of these problems in the workshop.
P 11-5
The elementary, irreversible gas-phase reaction
\ce{ A -> B + C }
is carried out adiabatically in a PFR packed with a catalyst. Pure A enters the reactor at a volumetric flow rate of 20 dm3/s, at a pressure of 10 atm, and a temperature of 450 K.
Additional information:
C_{P_A} = 40 J/mol \cdot K; C_{P_B} = 25 J/mol \cdot K; C_{P_C} = 15 J/mol \cdot K
H_A^{\circ} = -70 kJ/mol; H_B^{\circ} = -50 kJ/mol; H_C^{\circ} = -40 kJ/mol
All heats of formation are referenced to 273 K.
k = 0.133 \exp \left[ \frac{E}{R} \left( \frac{1}{450} - \frac{1}{T} \right) \right] \; \frac{dm^3}{kg-cat \cdot s} \; \text{with} \, E = 31.4 kJ/mol
Plot and then analyze the conversion and temperature down the plug-flow reactor until an 80% conversion (if possible) is reached. (The maximum catalyst weight that can be packed into the PFR is 50 kg.) Assume that \Delta P = 0.0.
Vary the inlet temperature and describe what you find.
Plot the heat that must be removed along the reactor ( Q vs. V) to maintain isothermal operation.
Now take the pressure drop into account in the PBR with \rho_b = 1 kg/dm^3. The reactor can be packed with one of two particle sizes. Choose one.
\alpha = 0.019/kg-cat \: \text{for particle diameter} \: D_1 \alpha = 0.0075/kg-cat \: \text{for particle diameter} \: D_2
- Plot and then analyze the temperature, conversion, and pressure along the length of the reactor. Vary the parameters \alpha and P_0 to learn the ranges of values in which they dramatically affect the conversion.
P 11-6
The irreversible endothermic vapor-phase reaction follows an elementary rate law
\ce{ CHECOCH3 -> CH2CO + CH4 }
\ce{ A -> B + C }
and is carried out adiabatically in a 500-dm3 PFR. Species A is fed to the reactor at a rate of 10 mol/min and a pressure of 2 atm. An inert stream is also fed to the reactor at 2 atm, as shown in Figure P11-6 B . The entrance temperature of both streams is 1100 K.
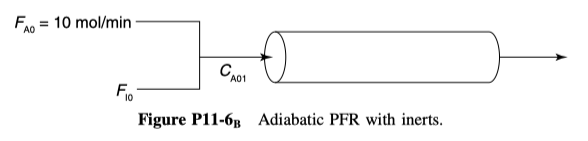
Additional information:
k = \exp (34.34 - 34222/T) dm^3/mol \cdot min (T in degrees Kelvin); C_{P_l} = 200 J/ mol \cdot K
C_{P_A} = 170 J/ mol \cdot K; C_{P_B} = 90 J/ mol \cdot K; C_{P_C} = 80 J/ mol \cdot K; \Delta H_{Rx}^\circ = 80000 J/ mol
First derive an expression for C_{A01} as a function of C_{A0} and \Phi_I.
Sketch the conversion and temperature profiles for the case when no inerts are present. Using a dashed line, sketch the profiles when a moderate amount of inerts are added. Using a dotted line, sketch the profiles when a large amount of inerts are added. Qualitative sketches are fine. Describe the similarities and differences between the curves.
Sketch or plot and then analyze the exit conversion as a function of \Phi_I. Is there a ratio of the entering molar flow rates of inerts (I) to A (i.e., \Phi_I = F_{I0}/ F_{A0} at which the conversion is at a maximum? Explain why there “is” or “is not” a maximum.
What would change in parts (b) and (c) if reactions were exothermic and reversible with \Delta H_{Rx}^{\circ} = -80 kJ/mol and K_C = 2 dm^3/mol at 1100 K?
Sketch or plot FB for parts (c) and (d), and describe what you find.
Plot the heat that must be removed along the reactor ( Q vs. V) to maintain isothermal operation for pure A fed and an exothermic reaction.
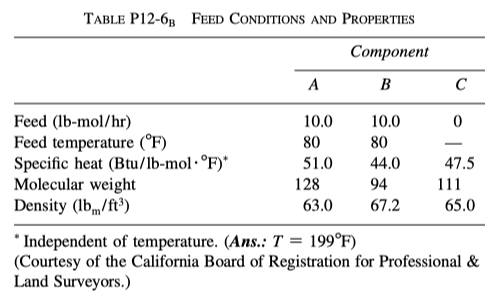
P 12-6
The endothermic liquid-phase elementary reaction
\ce { A + B -> 2 C }
proceeds, substantially, to completion in a single steam-jacketed, continuous-stirred reactor (Table P12-6 B ). From the following data, calculate the steady-state reactor temperature:
Reactor volume: 125 gal;
Steam jacket area: 10 ft2
Jacket steam: 150 psig (365.9 ^{\circ}F saturation temperature)
Overall heat-transfer coefficient of jacket, U: 150 Btu/h \cdot ft^2 \cdot ^{\circ}F
Agitator shaft horsepower: 25 hp
Heat of reaction, \Delta H_{Rx}^{\circ} = + 20000 Btu/lb-mol of A (independent of temperature)
P 12-21
The irreversible liquid-phase reactions
Reaction 1: \ce{A + B -> 2 C} \;\;\;\; r_{1C} = k_{1C} C_A C_B
Reaction 2: \ce{2 B + C -> D} \;\;\;\; r_{2D} = k_{2D} C_B C_C
are carried out in a PFR with heat exchange. The following temperature profiles were obtained for the reactor and the coolant stream:
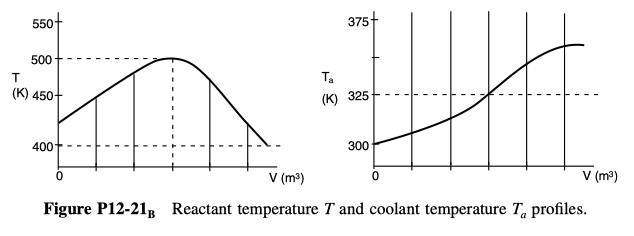
The concentrations of A, B, C, and D were measured at the point down the reactor where the liquid temperature, T, reached a maximum, and they were found to be CA = 0.1, CB = 0.2, CC= 0.5, and CD= 1.5, all in mol/dm3. The product of the overall heat-transfer coefficient and the heat-exchanger area per unit volume, Ua, is 10 cal/s \cdot dm^3 \cdot K. The entering molar flow rate of A is 10 mol/s.
Additional information
C_{P_A}= C_{P_B}=C_{P_C}=30 \, cal/mol/K \;\;\;\; C_{P_D}= 90 \, cal/mol/K, \;\;\;\; C_{P_I}=100 \, cal/mol/K
\Delta H_{Rx1A}^\circ = +5000 \, cal/ molA; \;\;\;\; k_{1C} = 0.043 (dm^3/mol \cdot s) at 400 K
\Delta H_{Rx2B}^\circ = +5000 \, cal/ molB; \;\;\;\; k_{2D} = 0.4 (dm^3/mol \cdot s) \exp 5000 K \left[ \frac{1}{500} - \frac{1}{T}\right]
- What is the activation energy for Reaction (1)?
Citation
@online{utikar2024,
author = {Utikar, Ranjeet},
title = {Workshop 07: {Non-isothermal} Reactor Design},
date = {2024-04-02},
url = {https://cre.smilelab.dev//content/workshops/07-non-isothermal-reactor-design},
langid = {en}
}