import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# Constants
R = 8.314 # J/mol K
TR = 273 # K
# A -> B + C
# 0: A; 1: B; 2: C
HF = np.array ([-70.0, -50.0, -40.])*1000 # J/mol
CP = np.array ([40.0, 25.0, 15.0]) # J/mol K
E = 31.4 * 1e3 # J/mol
k = lambda t: 0.133 * np.exp( (E/R) * (1/450.0 - 1/t) ) # dm3/ kgcat s
def pfr (w, x, *args):
X = x[0]
(ca0, fa0, T0, epsilon, delta_hr_tr, delta_cp, theta) = args
# Calculate T using energy balance
T = T0 + X * (-delta_hr_tr)/( np.sum(theta * CP) + X * delta_cp)
ca = ca0 * (( 1 - X ) / ( 1 + epsilon * X )) * (T0/T)
rate = k(T) * ca # -r_A
dxdw = rate/fa0
return [dxdw]
# Data
nu = np.array ([-1.0, 1.0, 1.0]) # stoichiometric coefficients
V_0 = 20 # dm3/s
P0 = 10 # atm
T0 = 450 # K
fa0 = P0 * V_0/ (R * T0)
ca0 = fa0/V_0
# inlet mole fraction
y0 = np.array ([1.0, 0.0, 0.0])
theta = np.array([1.0, 0.0, 0.0])
# Heat of reaction at 298K
delta_hr_tr = np.sum(HF * nu)
delta_cp = np.sum(CP * nu)
ya0 = y0[0]
epsilon = ya0 * np.sum(nu)
args = (ca0, fa0, T0, epsilon, delta_hr_tr, delta_cp, theta)
# initial condition
initial_conditions = np.array([0])
w_final = 50 # kg
sol = solve_ivp(pfr,
[0, w_final],
initial_conditions,
args=args,
dense_output=True)
w = np.linspace(0,w_final, 1000)
x = sol.sol(w)[0]
T = T0 + x * (-delta_hr_tr)/( np.sum(theta * CP) + x * delta_cp)Solutions to workshop 07: Non-isothermal reactor design
Lecture notes for chemical reaction engineering
Try following problems from Fogler 5e P 11-5, P 11-6, P 12-6, P 12-21
We will go through some of these problems in the workshop.
P 11-5
The elementary, irreversible gas-phase reaction
is carried out adiabatically in a PFR packed with a catalyst. Pure A enters the reactor at a volumetric flow rate of 20 dm3/s, at a pressure of 10 atm, and a temperature of 450 K.
Additional information:
; ;
; ;
All heats of formation are referenced to 273 K.
Plot and then analyze the conversion and temperature down the plug-flow reactor until an 80% conversion (if possible) is reached. (The maximum catalyst weight that can be packed into the PFR is 50 kg.) Assume that .
Vary the inlet temperature and describe what you find.
Plot the heat that must be removed along the reactor ( Q vs. V) to maintain isothermal operation.
Now take the pressure drop into account in the PBR with . The reactor can be packed with one of two particle sizes. Choose one.
- Plot and then analyze the temperature, conversion, and pressure along the length of the reactor. Vary the parameters and to learn the ranges of values in which they dramatically affect the conversion.
| Parameter | Value |
|---|---|
| 273.00 K | |
| 10.00 bar | |
| -20000.00 | |
| 0.00 | |
| 1.00 | |
| 2.673e-03 | |
| 0.053 mol/s |
Energy balance:
T = 450.00 + 500.00 X
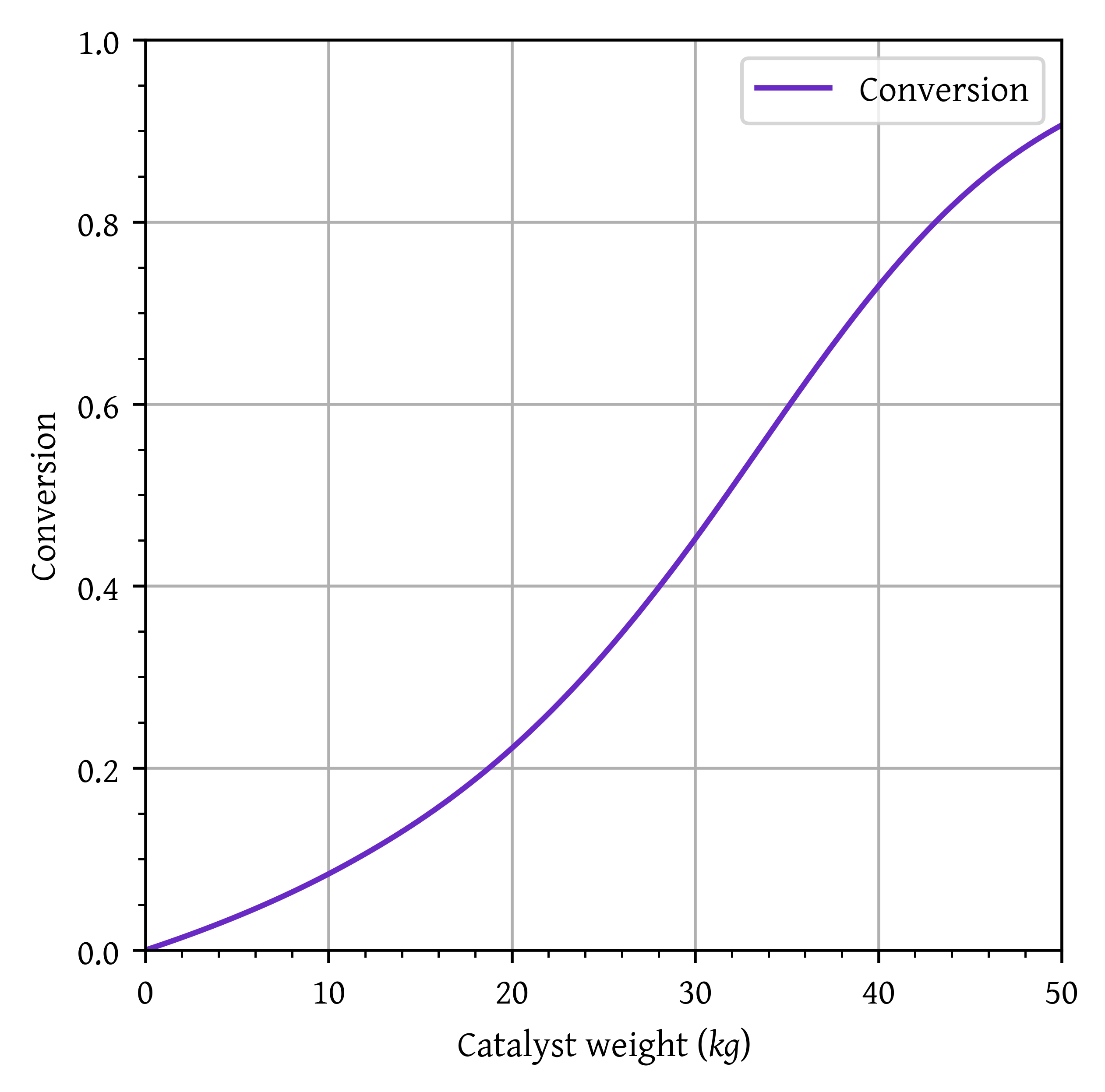
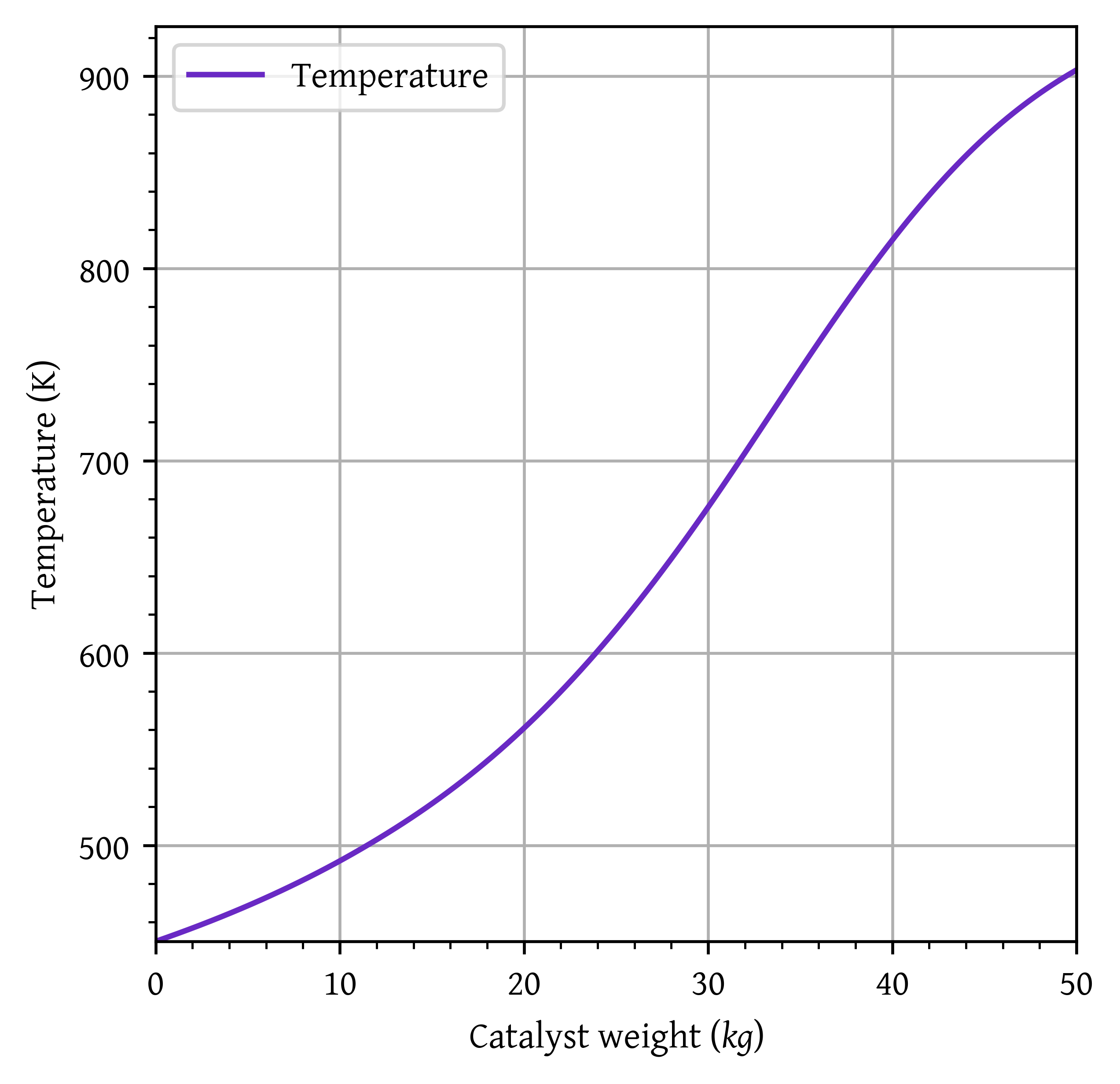
Catalyst weight required to achieve 80% conversion: 43.14 kg
Temperature at 80% conversion: 850.18 K
Exit (W = 50.00 kg) conversion: 0.91
Exit (W = 50.00 kg) temperature: 903.19 K
plt.plot(w,x, label="Conversion")
plt.xlim(0,50)
plt.ylim(0,1)
plt.grid()
plt.legend()
plt.xlabel('Catalyst weight ($kg$)')
plt.ylabel('Conversion')
plt.show()plt.plot(w,T, label='Temperature')
plt.xlim(0,50)
head_margin = (np.max(T) - np.min(T)) * 0.05
ylim_lower = np.min(T)
ylim_upper = np.max(T) + head_margin
plt.ylim(ylim_lower, ylim_upper)
plt.grid()
plt.legend()
plt.xlabel('Catalyst weight ($kg$)')
plt.ylabel('Temperature (K)')
plt.show()Effect of temperature
T0_range = np.arange(400, 501, 1)
X_final = np.zeros(len(T0_range))
T_final = np.zeros(len(T0_range))
W_p8 = np.zeros(len(T0_range))
for i in range(len(T0_range)):
T0 = T0_range[i]
args = (ca0, fa0, T0, epsilon, delta_hr_tr, delta_cp, theta)
# initial condition
initial_conditions = np.array([0])
w_final = 50 # kg
sol = solve_ivp(pfr,
[0, w_final],
initial_conditions,
args=args,
dense_output=True)
w = np.linspace(0,w_final, 1000)
x = sol.sol(w)[0]
T = T0 + x * (-delta_hr_tr)/( np.sum(theta * CP) + x * delta_cp)
# add values to array for reporting
X_final[i] = x[-1]
T_final[i] = T[-1]
# see if you reach 80% conversion
if x[-1] > 0.8:
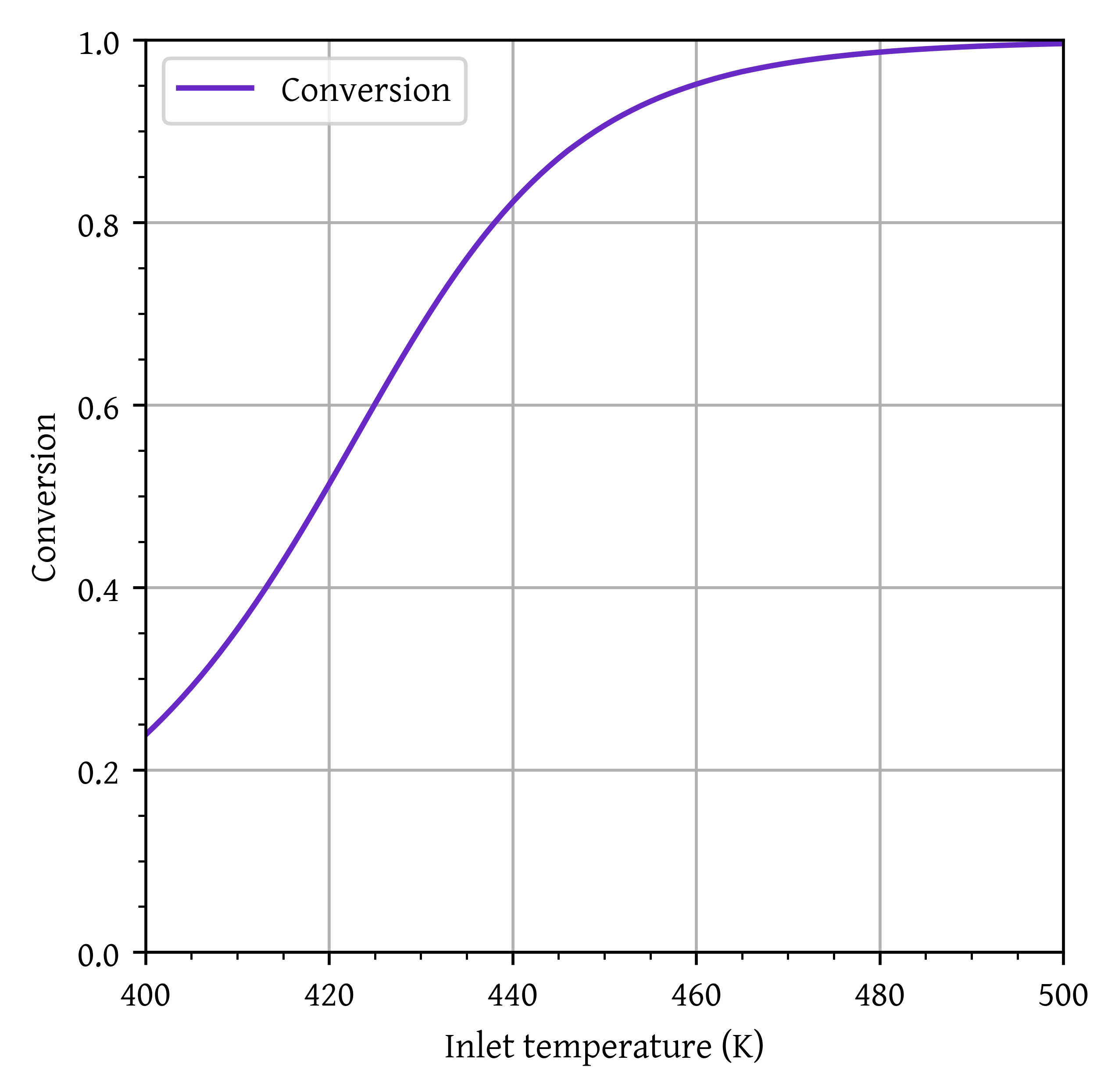
W_p8[i] = w[x>0.8][0]plt.plot(T0_range,X_final, label='Conversion')
plt.xlim(T0_range[0],T0_range[-1])
plt.ylim(0,1)
plt.grid()
plt.legend()
plt.xlabel('Inlet temperature (K)')
plt.ylabel('Conversion')
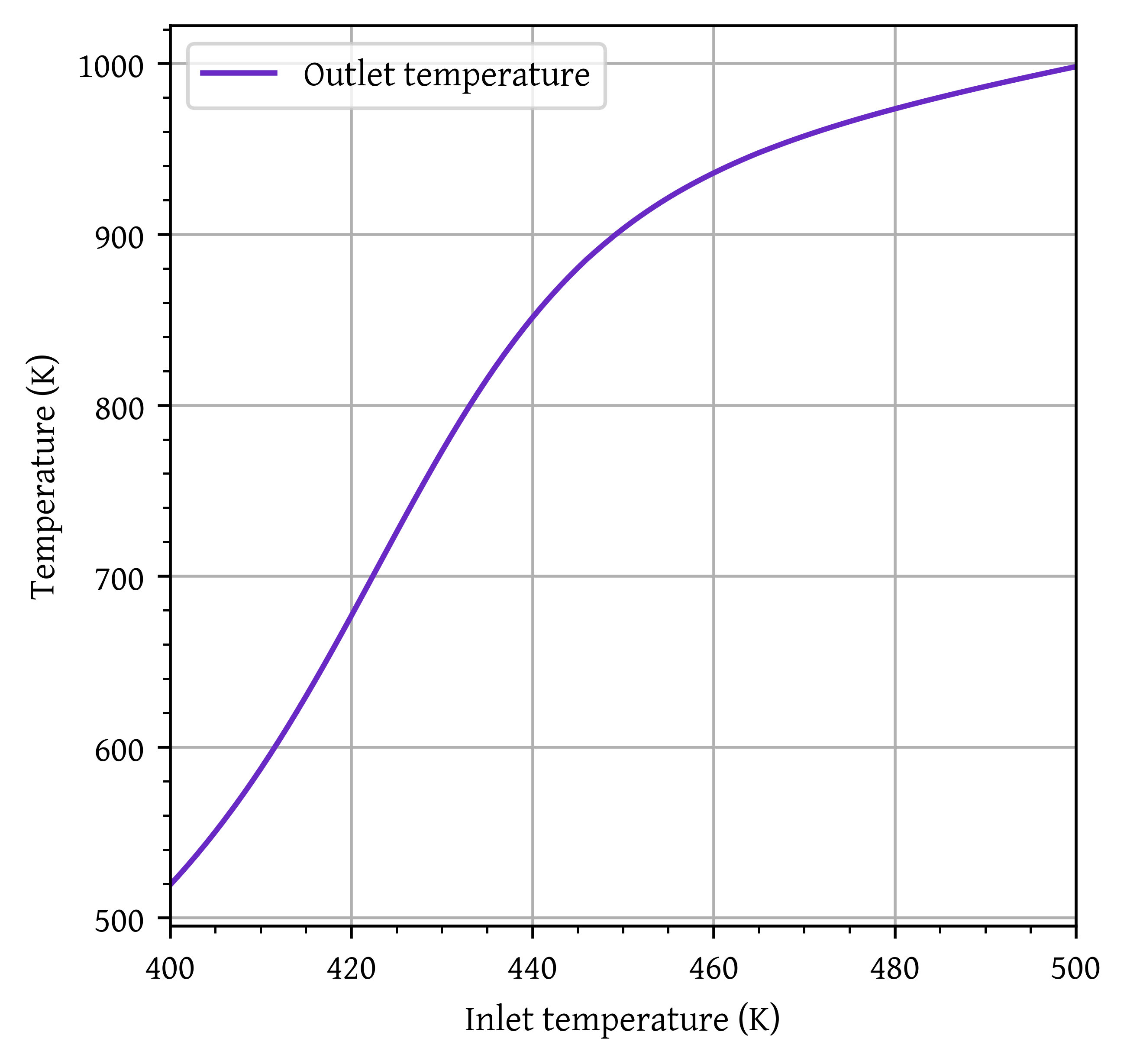
plt.show()plt.plot(T0_range,T_final, label='Outlet temperature')
plt.xlim(T0_range[0],T0_range[-1])
head_margin = (np.max(T_final) - np.min(T_final)) * 0.05
ylim_lower = np.min(T_final) - head_margin
ylim_upper = np.max(T_final) + head_margin
print (np.max(T_final) + head_margin)
plt.ylim(ylim_lower, ylim_upper)
plt.grid()
plt.legend()
plt.xlabel('Inlet temperature (K)')
plt.ylabel('Temperature (K)')
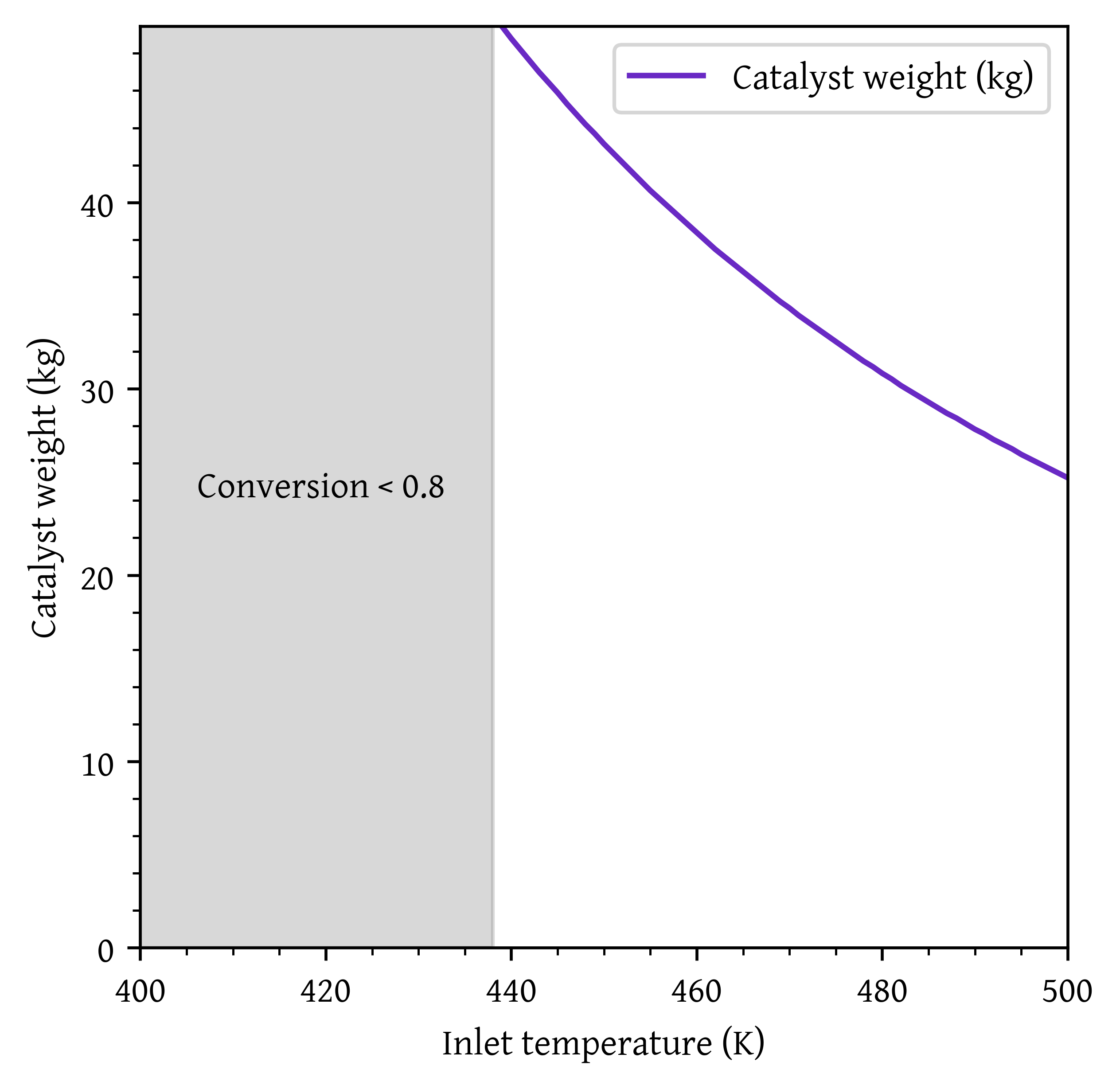
plt.show()1022.0467173119888plt.plot(T0_range[W_p8 > 0], W_p8[W_p8 > 0], label='Catalyst weight (kg)')
plt.xlim(T0_range[0],T0_range[-1])
plt.ylim(np.min(W_p8), np.max(W_p8))
plt.legend()
plt.xlabel('Inlet temperature (K)')
plt.ylabel('Catalyst weight (kg)')
plt.fill_between(T0_range, 0, 1,
where=W_p8==0,
color='gray',
alpha=0.3,
transform=plt.gca().get_xaxis_transform())
x_pos = np.min(T0_range) + 0.5 * (T0_range[W_p8 > 0][0] - np.min(T0_range))
y_pos = np.min(W_p8) + 0.5 * (np.max(W_p8) - np.min(W_p8))
plt.text(x_pos, y_pos,
'Conversion < 0.8',
horizontalalignment='center',
verticalalignment='center',
color='black',
fontsize=10)
plt.show()Minimum inlet temperature required to achieve 80% conversion: 439 K
Heat that must be removed along the reactor to maintain isothermal operation:
T0 = 450
args = (ca0, fa0, T0, epsilon, delta_hr_tr, delta_cp, theta)
# initial condition
initial_conditions = np.array([0])
w_final = 50 # kg
sol = solve_ivp(pfr,
[0, w_final],
initial_conditions,
args=args,
dense_output=True)
w = np.linspace(0,w_final, 1000)
x = sol.sol(w)[0]
T = T0 + x * (-delta_hr_tr)/( np.sum(theta * CP) + x * delta_cp)
delta_h = delta_hr_tr + delta_cp * (T - TR)
ca = ca0 * (( 1 - x ) / ( 1 + epsilon * x )) * (T0/T)
rate = k(T) * ca # -r_A
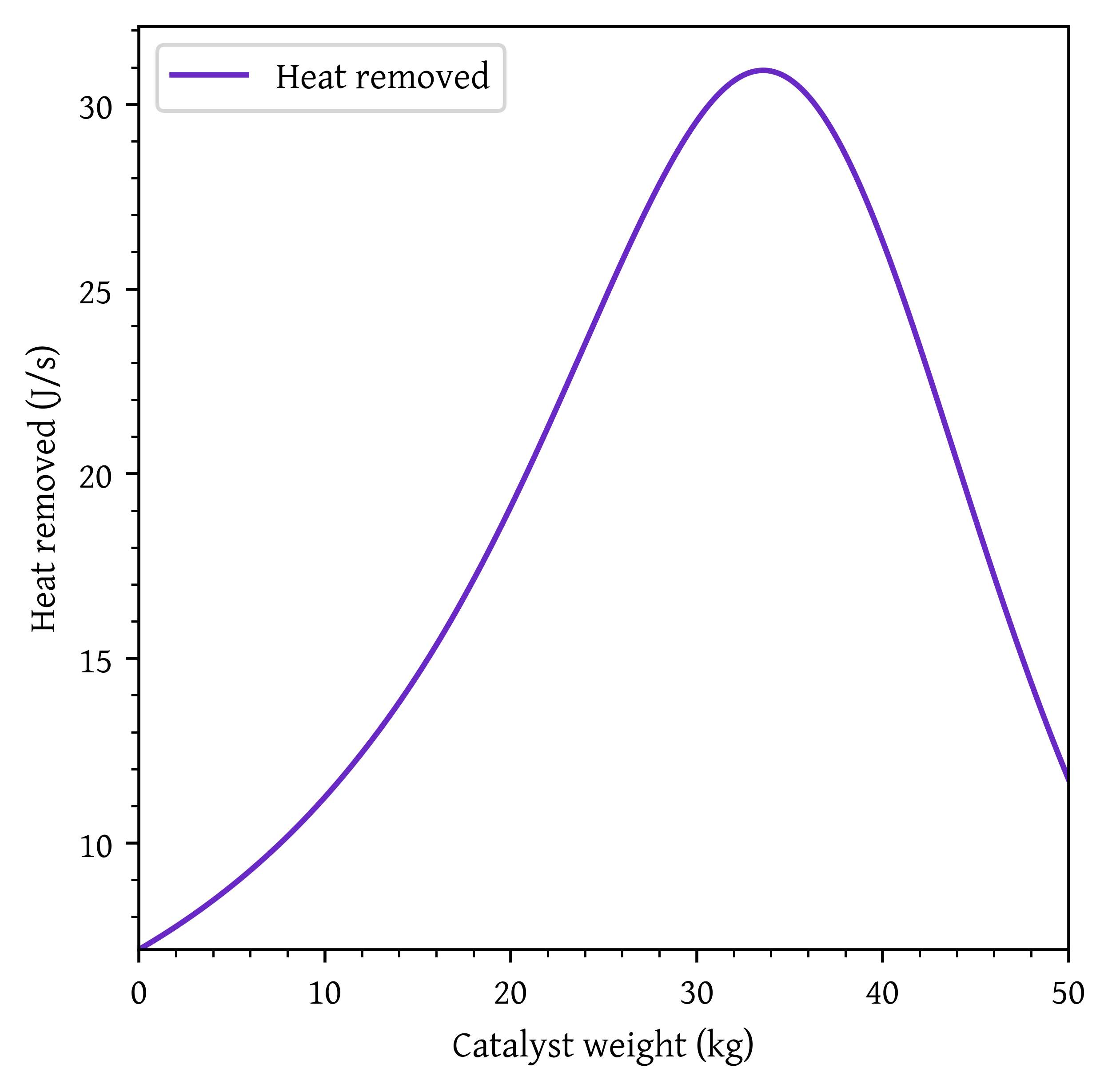
heat_removed = -rate*delta_hplt.plot(w, heat_removed, label='Heat removed')
plt.xlim(np.min(w), np.max(w))
head_margin = (np.max(heat_removed) - np.min(heat_removed)) * 0.05
ylim_upper = np.max(heat_removed) + head_margin
plt.ylim(np.min(heat_removed), ylim_upper)
plt.legend()
plt.xlabel('Catalyst weight (kg)')
plt.ylabel('Heat removed (J/s)')
plt.show()Pressure drop:
def pfr_with_pressure_drop (w, x, *args):
X,p = x
(ca0, fa0, T0, epsilon, delta_hr_tr, delta_cp, theta, alpha) = args
# Calculate T using energy balance
T = T0 + X * (-delta_hr_tr)/( np.sum(theta * CP) + X * delta_cp)
ca = ca0 * p * (( 1 - X ) / ( 1 + epsilon * X )) * (T0/T)
rate = k(T) * ca # -r_A
dxdw = rate/fa0
dpdw = -(alpha/2*p) * (T/T0) * (1 + epsilon * X)
return [dxdw, dpdw]T0 = 450
# initial condition
initial_conditions = np.array([0.0, 1.0])
w_final = 50 # kg
alpha1 = 0.0075 # 1/kg
args = (ca0, fa0, T0, epsilon, delta_hr_tr, delta_cp, theta, alpha1)
sol1 = solve_ivp(pfr_with_pressure_drop,
[0, w_final],
initial_conditions,
args=args,
dense_output=True)
w = np.linspace(0,w_final, 1000)
x1 = sol1.sol(w)[0]
T1 = T0 + x1 * (-delta_hr_tr)/( np.sum(theta * CP) + x1 * delta_cp)
p1 = sol1.sol(w)[1]
alpha2 = 0.019 # 1/kg
args = (ca0, fa0, T0, epsilon, delta_hr_tr, delta_cp, theta, alpha2)
sol2 = solve_ivp(pfr_with_pressure_drop,
[0, w_final],
initial_conditions,
args=args,
dense_output=True)
w = np.linspace(0,w_final, 1000)
x2 = sol2.sol(w)[0]
T2 = T0 + x2 * (-delta_hr_tr)/( np.sum(theta * CP) + x2 * delta_cp)
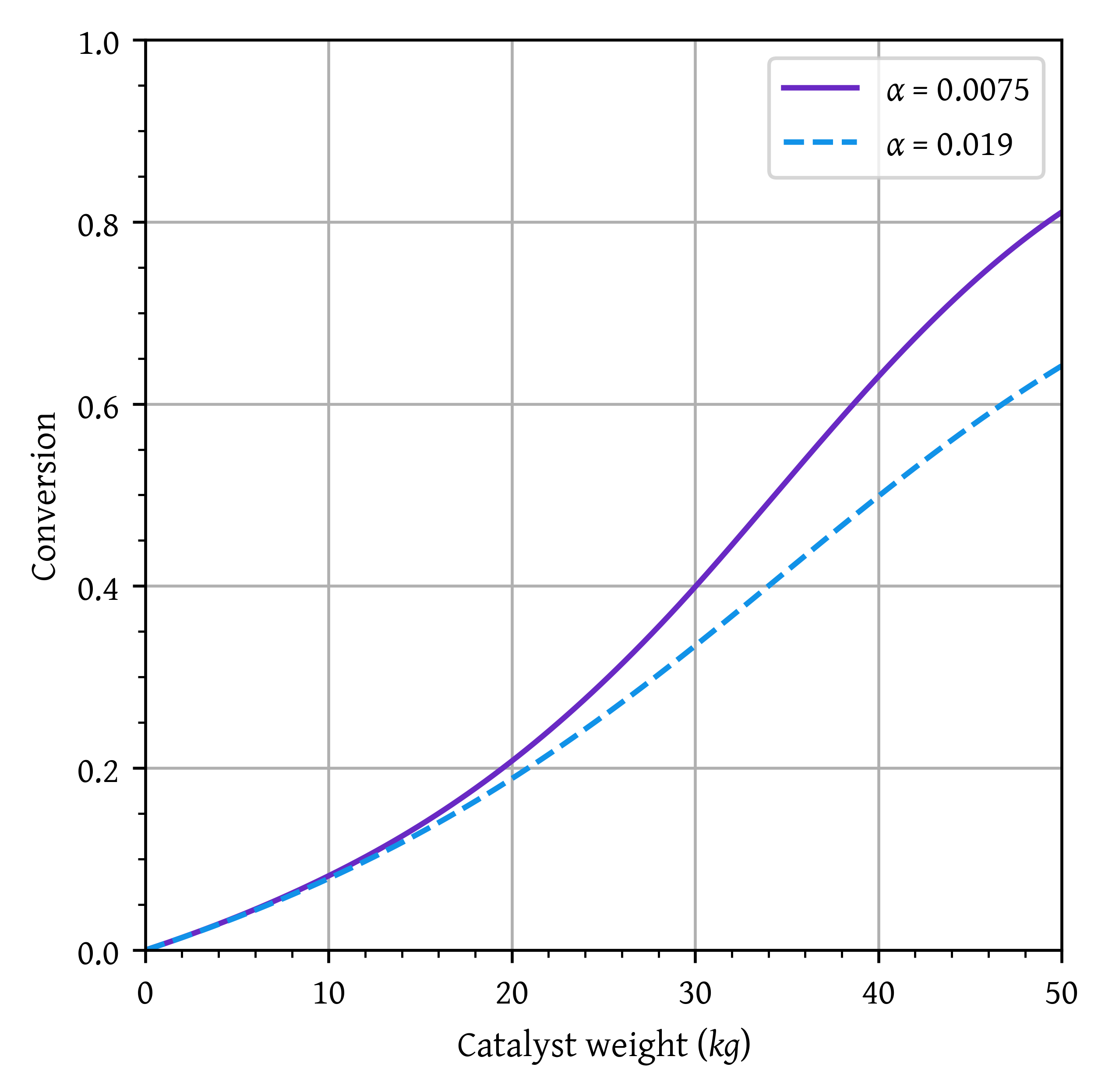
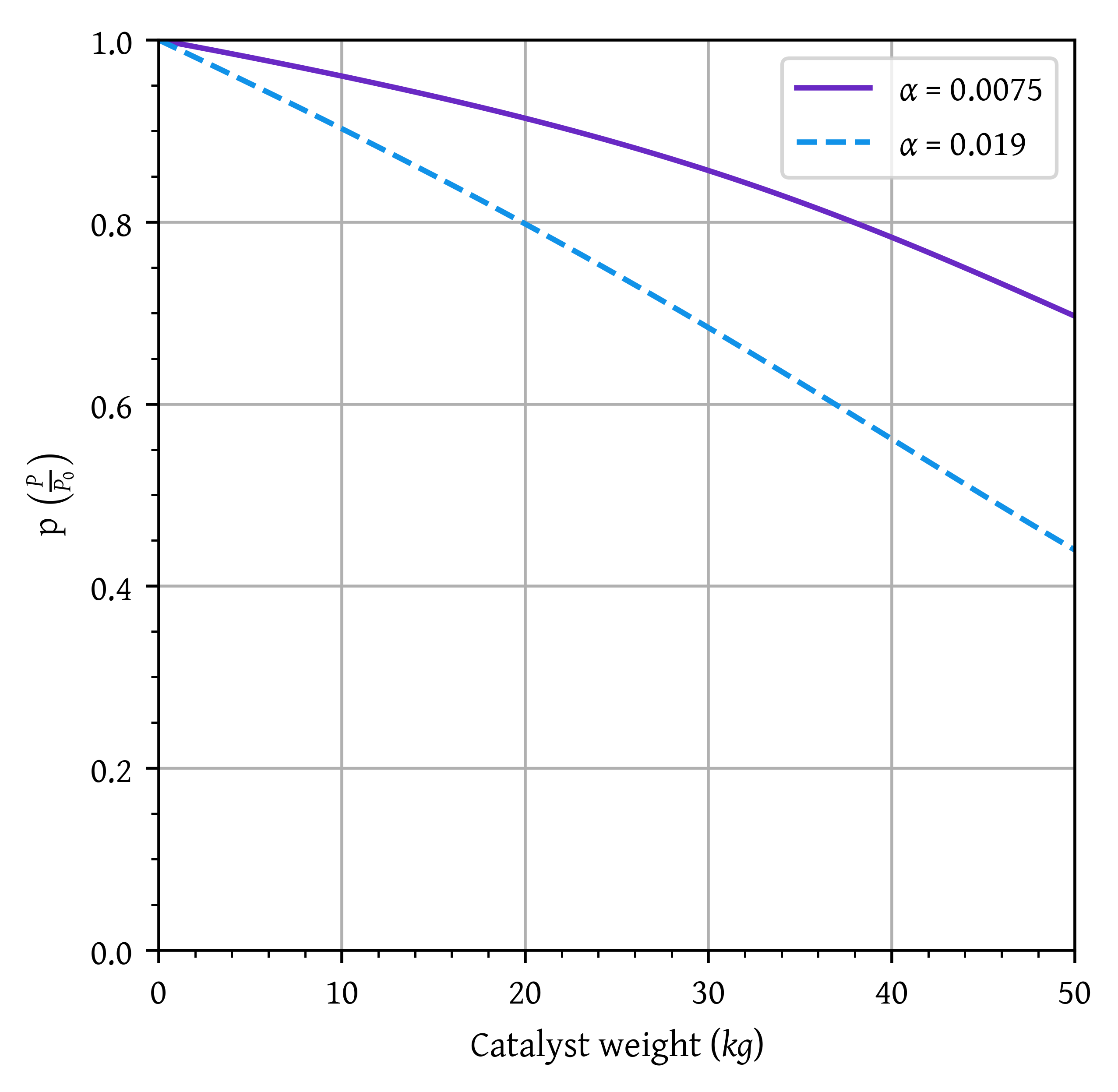
p2 = sol2.sol(w)[1]plt.plot(w,x1, label=f'$\\alpha$ = {alpha1}')
plt.plot(w,x2, label=f'$\\alpha$ = {alpha2}')
plt.xlim(0,50)
plt.ylim(0,1)
plt.grid()
plt.legend()
plt.xlabel('Catalyst weight ($kg$)')
plt.ylabel('Conversion')
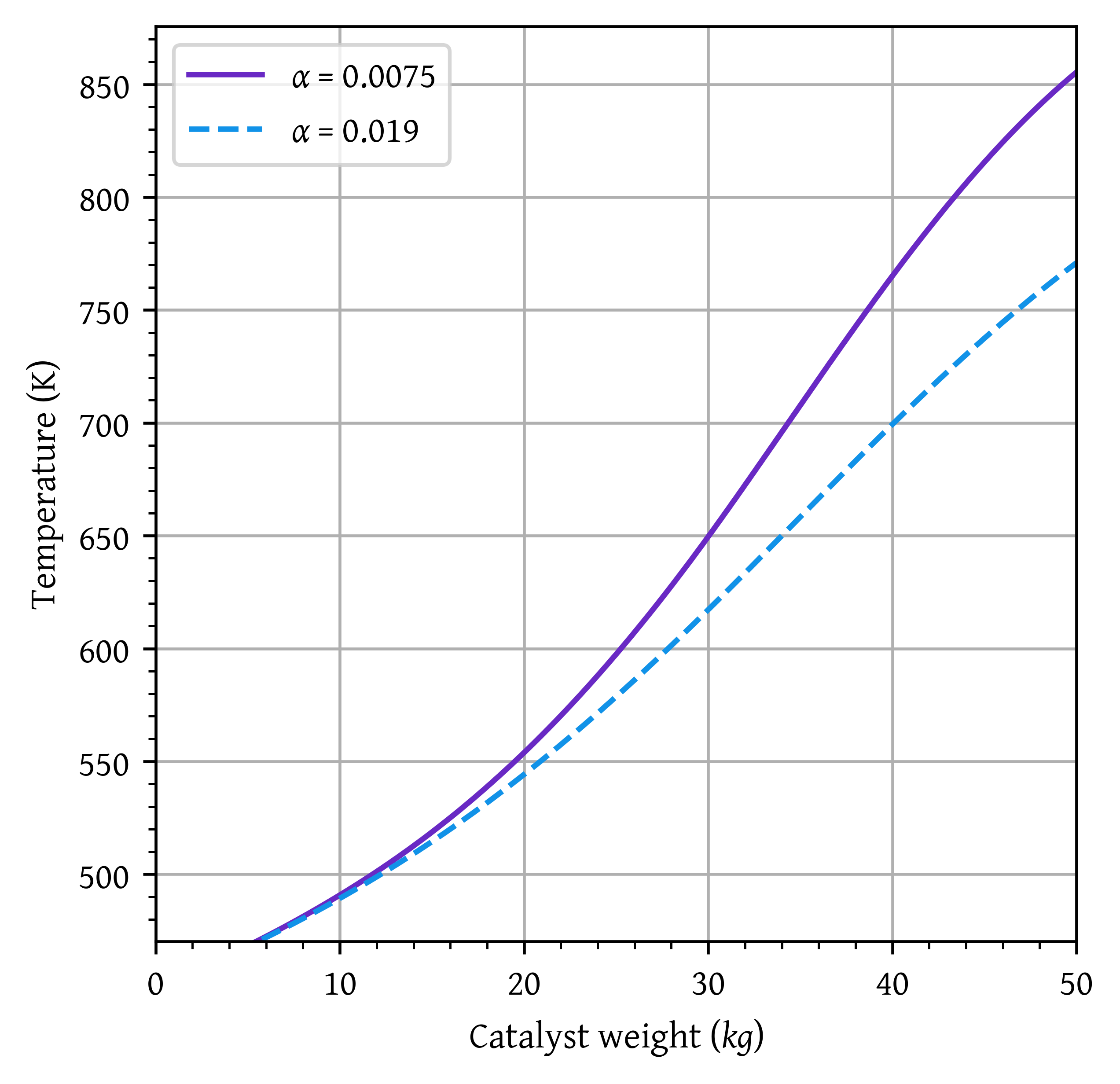
plt.show()plt.plot(w,T1, label=f'$\\alpha$ = {alpha1}')
plt.plot(w,T2, label=f'$\\alpha$ = {alpha2}')
plt.xlim(0,50)
min_t = np.min(np.concatenate((T1, T2)))
max_t = np.max(np.concatenate((T1, T2)))
head_margin = (max_t - min_t) * 0.05
ylim_lower = min_t + head_margin
ylim_upper = max_t + head_margin
plt.ylim(ylim_lower, ylim_upper)
plt.grid()
plt.legend()
plt.xlabel('Catalyst weight ($kg$)')
plt.ylabel('Temperature (K)')
plt.show()P 11-6
The irreversible endothermic vapor-phase reaction follows an elementary rate law
and is carried out adiabatically in a 500-dm3 PFR. Species A is fed to the reactor at a rate of 10 mol/min and a pressure of 2 atm. An inert stream is also fed to the reactor at 2 atm, as shown in Figure P11-6 B . The entrance temperature of both streams is 1100 K.
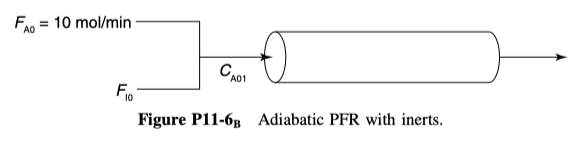
Additional information:
(T in degrees Kelvin);
; ; ;
First derive an expression for as a function of and .
Sketch the conversion and temperature profiles for the case when no inerts are present. Using a dashed line, sketch the profiles when a moderate amount of inerts are added. Using a dotted line, sketch the profiles when a large amount of inerts are added. Qualitative sketches are fine. Describe the similarities and differences between the curves.
Sketch or plot and then analyze the exit conversion as a function of . Is there a ratio of the entering molar flow rates of inerts (I) to A (i.e., at which the conversion is at a maximum? Explain why there “is” or “is not” a maximum.
What would change in parts (b) and (c) if reactions were exothermic and reversible with and at 1100 K?
Sketch or plot FB for parts (c) and (d), and describe what you find.
Plot the heat that must be removed along the reactor ( Q vs. V) to maintain isothermal operation for pure A fed and an exothermic reaction.
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
from scipy.optimize import minimize
k116 = lambda t: np.exp(34.34 - 34222/t)
def pfr116 (V, x, *args):
X = x[0]
(ca0, fa0, T0, epsilon, delta_hr_tr, sumCp) = args
# Calculate T using energy balance
T = (- delta_hr_tr * X + sumCp* T0)/(sumCp)
ca = ca0 * (( 1 - X ) / ( 1 + epsilon * X )) * (T0/T)
rate = k116(T) * ca # -r_A
dxdw = rate/fa0
return [dxdw]
# data
R = 0.082 # dm^3 atm / mol K
# A -> B + C
cpA = 170 #J/mol K
cpB = 90 #J/mol K
cpC = 80 #J/mol K
cpI = 200 #J/mol K
delta_hr_tr = 80000 # J/mol
volume = 500 # dm^3
fa0 = 10 # mol/min
P0 = 2 # atm
T0 = 1100 # K
results = {}
thetaIs = [0, 10, 100]
for thetaI in thetaIs:
fi0 = fa0 * thetaI # mol/min
ft = fa0 + fi0
ca0 = P0/(R * T0)
ci0 = P0/(R * T0)
ca01 = (ca0 + ci0)/(thetaI + 1)
epsilon = 1/(1 + thetaI)
sumCp = cpA + cpI * thetaI
args = (ca01, fa0, T0, epsilon, delta_hr_tr, sumCp)
initial_conditions = np.array([0.0])
sol116 = solve_ivp(pfr116,
[0, volume],
initial_conditions,
args=args,
dense_output=True)
v = np.linspace(0,volume, 1000)
x = sol116.sol(v)[0]
T = (- delta_hr_tr * x + sumCp* T0)/(sumCp)
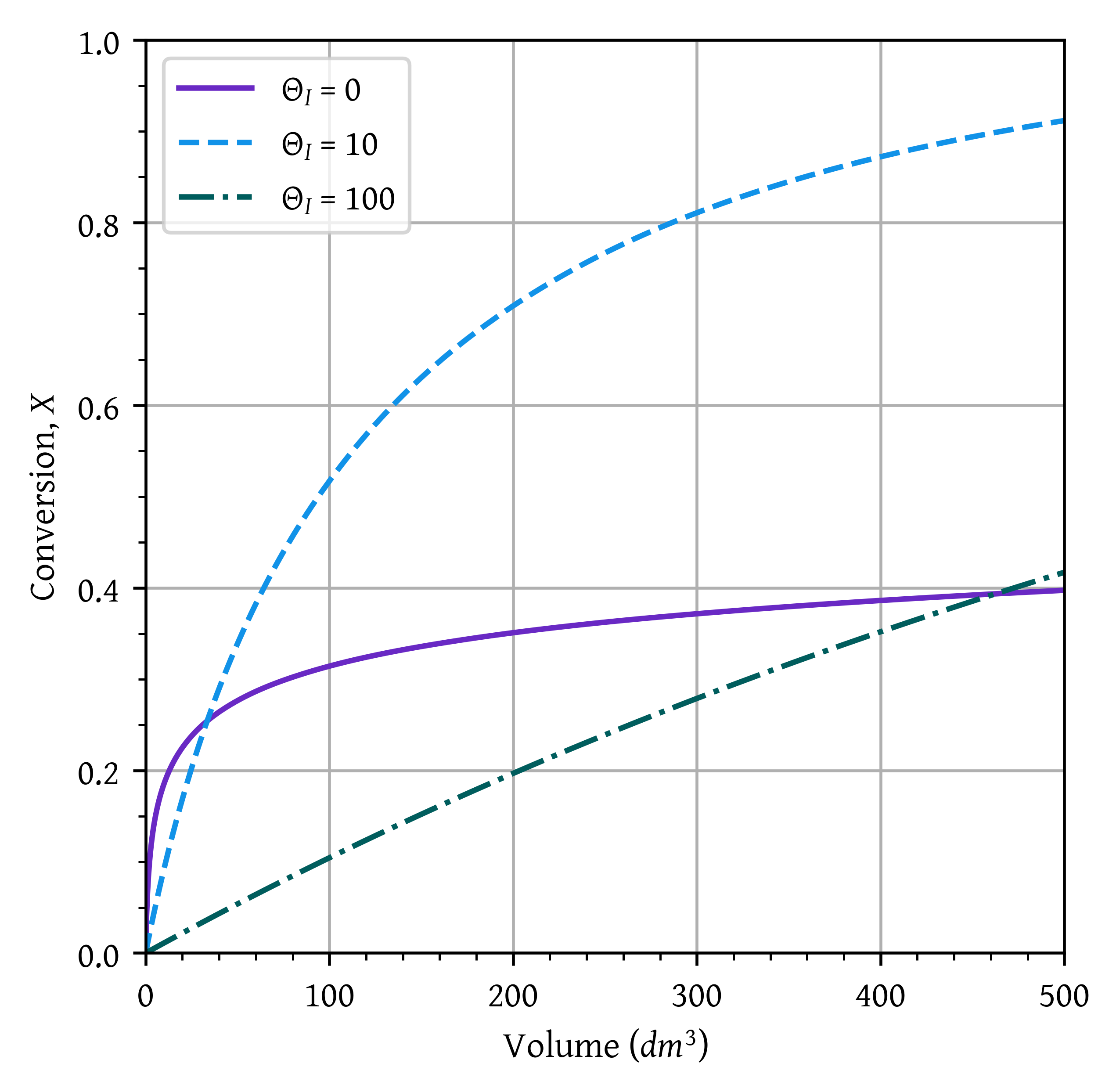
results[thetaI] = {'v': v, 'x': x, 'T': T}for thetaI, data in results.items():
plt.plot(data['v'],
data['x'],
label=f'$\\Theta_I$ = {thetaI}')
plt.xlim(0,volume)
plt.ylim(0,1)
plt.grid()
plt.legend()
plt.xlabel('Volume ($dm^3$)')
plt.ylabel('Conversion, $X$')
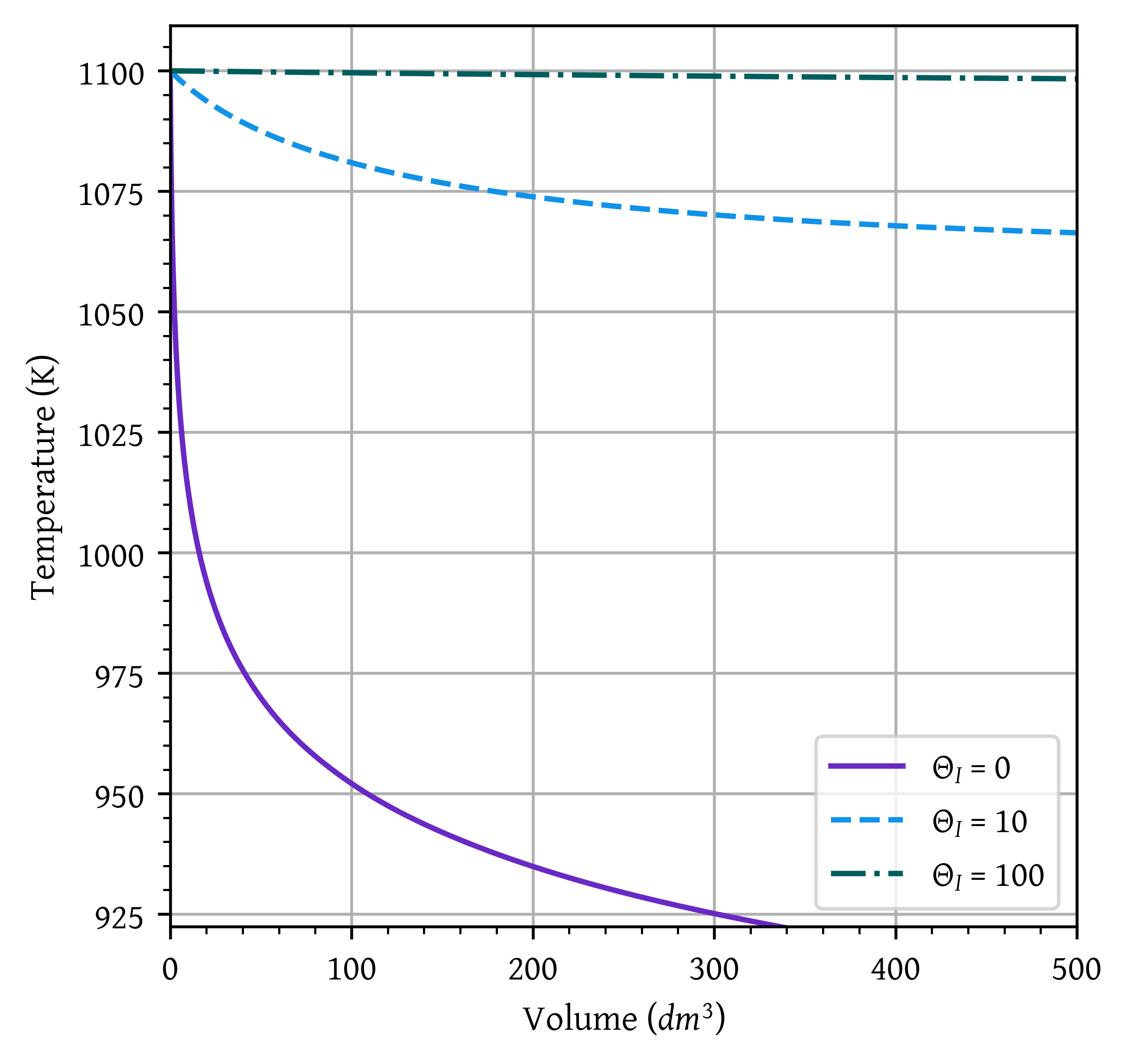
plt.show()min_t = []
max_t = []
for thetaI, data in results.items():
v = data['v']
T = data['T']
plt.plot(v, T,
label=f'$\\Theta_I$ = {thetaI}')
m = np.min(T)
min_t.append(m)
m = np.max(T)
max_t.append(m)
plt.xlim(0,volume)
min_temp = np.min(min_t)
max_temp = np.max(max_t)
head_margin = (max_temp - min_temp) * 0.05
ylim_lower = min_temp + head_margin
ylim_upper = max_temp + head_margin
plt.ylim(ylim_lower,ylim_upper)
plt.grid()
plt.legend()
plt.xlabel('Volume ($dm^3$)')
plt.ylabel('Temperature (K)')
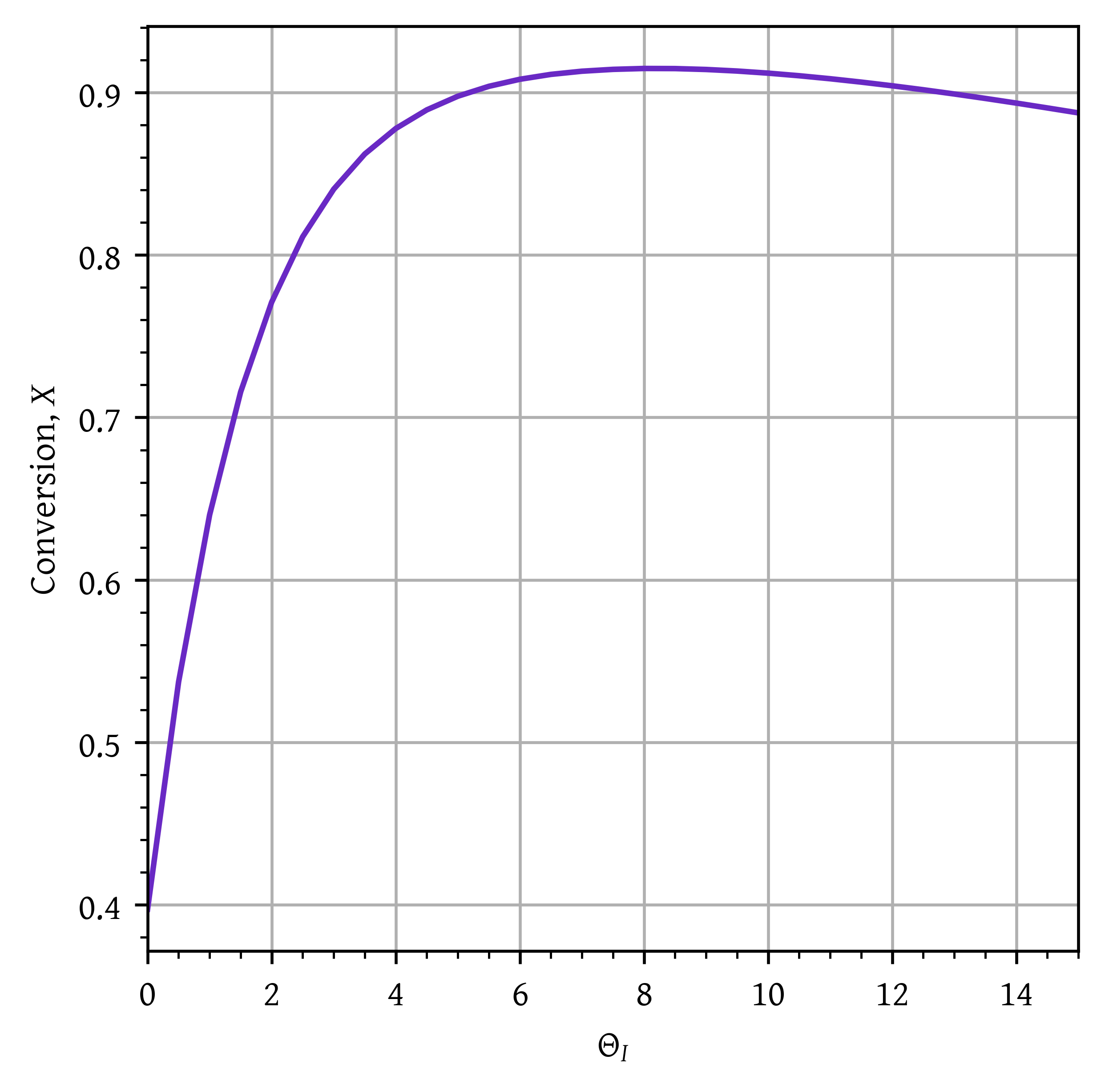
plt.show()Optimal :
thetaIs = np.arange(0,15 + 0.5,0.5)
conv = []
for thetaI in thetaIs:
fi0 = fa0 * thetaI # mol/min
ft = fa0 + fi0
ca0 = P0/(R * T0)
ci0 = P0/(R * T0)
ca01 = (ca0 + ci0)/(thetaI + 1)
epsilon = 1/(1 + thetaI)
sumCp = cpA + cpI * thetaI
args = (ca01, fa0, T0, epsilon, delta_hr_tr, sumCp)
initial_conditions = np.array([0.0])
sol116 = solve_ivp(pfr116,
[0, volume],
initial_conditions,
args=args,
dense_output=True)
v = np.linspace(0,volume, 1000)
x = sol116.sol(v)[0]
T = (- delta_hr_tr * x + sumCp* T0)/(sumCp)
conv.append(x[-1])
plt.plot(thetaIs,conv)
plt.xlim(np.min(thetaIs), np.max(thetaIs))
min_x = np.min(conv)
max_x = np.max(conv)
head_margin = (max_x - min_x) * 0.05
ylim_lower = min_x + head_margin
ylim_upper = max_x + head_margin
plt.grid()
plt.xlabel('$\\Theta_I$')
plt.ylabel('Conversion, $X$')
plt.show()def objective(thetaI):
ca0 = P0 / (R * T0)
ci0 = P0 / (R * T0)
ca01 = (ca0 + ci0) / (thetaI + 1)
epsilon = 1 / (1 + thetaI)
sumCp = cpA + cpI * thetaI
args = (ca01, fa0, T0, epsilon, delta_hr_tr, sumCp)
initial_conditions = np.array([0.0])
sol = solve_ivp(pfr116, [0, volume], initial_conditions, args=args, dense_output=True)
final_x = sol.y[0, -1] # Get the final conversion
return -final_x # Minimize the negative of the final conversion to maximize it
# Constants
R = 0.082 # dm^3 atm / mol K
cpA = 170 # J/mol K
cpI = 200 # J/mol K
delta_hr_tr = 80000 # J/mol
volume = 500 # dm^3
fa0 = 10 # mol/min
P0 = 2 # atm
T0 = 1100 # K
# Optimization setup
thetaI_bounds = (0, 100) # Define bounds for thetaI as a tuple (min, max)
result = minimize(objective, x0=[10], bounds=[thetaI_bounds], method='L-BFGS-B')
# Display results
optimal_thetaI = result.x[0]The optimal is 8.187. Maximum conversion = 0.915
P 12-6
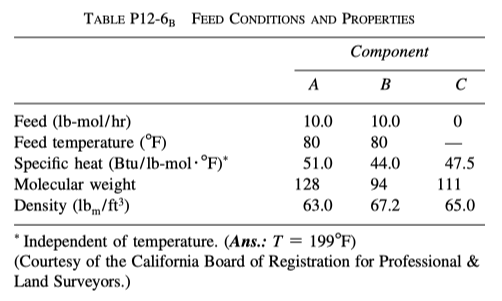
The endothermic liquid-phase elementary reaction
proceeds, substantially, to completion in a single steam-jacketed, continuous-stirred reactor (Table P12-6 B ). From the following data, calculate the steady-state reactor temperature:
Reactor volume: 125 gal;
Steam jacket area: 10 ft2
Jacket steam: 150 psig (365.9 F saturation temperature)
Overall heat-transfer coefficient of jacket, U: 150
Agitator shaft horsepower: 25 hp
Heat of reaction, Btu/lb-mol of A (independent of temperature)
P 12-21
The irreversible liquid-phase reactions
Reaction 1:
Reaction 2:
are carried out in a PFR with heat exchange. The following temperature profiles were obtained for the reactor and the coolant stream:
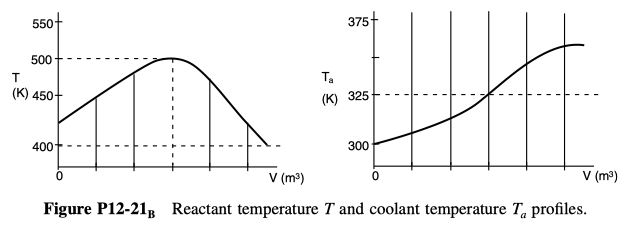
The concentrations of A, B, C, and D were measured at the point down the reactor where the liquid temperature, T, reached a maximum, and they were found to be CA = 0.1, CB = 0.2, CC= 0.5, and CD= 1.5, all in mol/dm3. The product of the overall heat-transfer coefficient and the heat-exchanger area per unit volume, Ua, is 10 . The entering molar flow rate of A is 10 mol/s.
Additional information
,
; at 400 K
;
- What is the activation energy for Reaction (1)?
Citation
@online{utikar2024,
author = {Utikar, Ranjeet},
title = {Solutions to Workshop 07: {Non-isothermal} Reactor Design},
date = {2024-03-24},
url = {https://cre.smilelab.dev/content/workshops/07-non-isothermal-reactor-design/solutions.html},
langid = {en}
}