import sympy as sp
from IPython.display import display, Markdown
# Define variables
t, u= sp.symbols('t, u')
tau = sp.symbols('tau', real=True, positive=True)
et = sp.sqrt(tau**2 - (t - tau)**2)
# using u = t - tau integral becomes
# E(t) = int from -tau to tau ( sqrt (tau^2 - u^2))
integral_eu = sp.integrate(sp.sqrt(tau**2 - u**2), (u, -tau, tau))
tau_est = sp.solve(integral_eu - 1, tau)
# Evaluate the numeric value of tau_est
tau_numeric = tau_est[0].evalf()Solutions to workshop 11: Distribution of residence time
Lecture notes for chemical reaction engineering
Try following problems from Fogler 5e (Fogler (2016)) P 16-3, P 16-6, P 16-11
We will go through some of these problems in the workshop.
P 16-3
Consider the curve below.
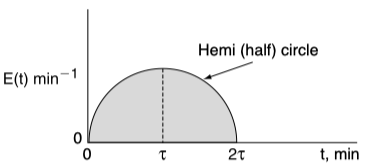
Mathematically this hemi circle is described by these equations:
For , then min–1 (hemi circle)
For , then
What is the mean residence time?
What is the variance?
Integral of :
integral_latex = sp.latex(integral_eu)
display(Markdown(f"$$E(t) = {integral_latex}$$"))
Solution for
tau_latex = sp.latex(sp.simplify(tau_est[0]))
display(Markdown(f"$$\\tau = {tau_latex}$$"))
= 0.798 min.
We can also solve this problem numerically
import numpy as np
from scipy.integrate import quad
from scipy.optimize import fsolve
from IPython.display import display, Markdown
# Define E(t) function
def et(t, tau):
if 0 <= t <= 2 * tau:
return np.sqrt(tau**2 - (t - tau)**2)
else:
return 0
# Function to find tau such that the integral equals 1
def integral(tau):
res, _ = quad(et, 0, 2 * tau, args=(tau,))
return res - 1
# Initial guess for tau
tau_guess = 1
# Solve for tau
tau_est = fsolve(integral, tau_guess)[0]
# Define the variance function
def variance_func(t, tau):
return (t - tau)**2 * et(t, tau)
# Calculate the variance using numerical integration
variance_value, _ = quad(variance_func, 0, 2 * tau_est, args=(tau_est,))Using numerical method:
0.798 min.
0.159 min2.
P 16-6
An RTD experiment was carried out in a nonideal reactor that gave the following results:
| for | ||
| for | ||
| for |
What are the mean residence time, , and variance ?
What is the fraction of the fluid that spends a time 1.5 minutes or longer in the reactor?
What fraction of fluid spends 2 minutes or less in the reactor?
What fraction of fluid spends between 1.5 and 2 minutes in the reactor?
Hand written solution, (Accompanying excel file).
import numpy as np
from scipy.integrate import quad
from IPython.display import display, Markdown
# Define E(t) function
def et(t):
if t < 1:
return 0
elif 1 <= t <= 2:
return 1.0
else:
return 0
# Mean residence time function
def tau_func(t):
return t * et(t)
# Variance function
def variance_func(t, tm):
return (t - tm)**2 * et(t)
# Calculate mean residence time (t_m)
tau, _ = quad(tau_func, 0, np.inf)
# Calculate variance (sigma^2)
variance, _ = quad(variance_func, 0, np.inf, args=(tau,))
# Fraction of fluid that spends 1.5 minutes or longer
f1_5_inf, _ = quad(et, 1.5, np.inf)
# Fraction of fluid that spends 2 minutes or less
f0_2, _ = quad(et, 0, 2)
# Fraction of fluid that spends between 1.5 and 2 minutes
f1_5_2, _ = quad(et, 1.5, 2)Mean Residence Time 1.5000 min.
Variance 0.0833 .
Fraction of fluid that spends 1.5 minutes or longer: 0.50
Fraction of fluid that spends 2 minutes or less: 1.00
Fraction of fluid that spends between 1.5 and 2 minutes: 0.50
P 16-11
The volumetric flow rate through a reactor is 10 dm3/min. A pulse test gave the following concentration measurements at the outlet:
| t (min) | t (min) | ||
|---|---|---|---|
| 0 | 0 | 15 | 238 |
| 0.4 | 329 | 20 | 136 |
| 1.0 | 622 | 25 | 77 |
| 2 | 812 | 30 | 44 |
| 3 | 831 | 35 | 25 |
| 4 | 785 | 40 | 14 |
| 5 | 720 | 45 | 8 |
| 6 | 650 | 50 | 5 |
| 8 | 523 | 60 | 1 |
| 10 | 418 |
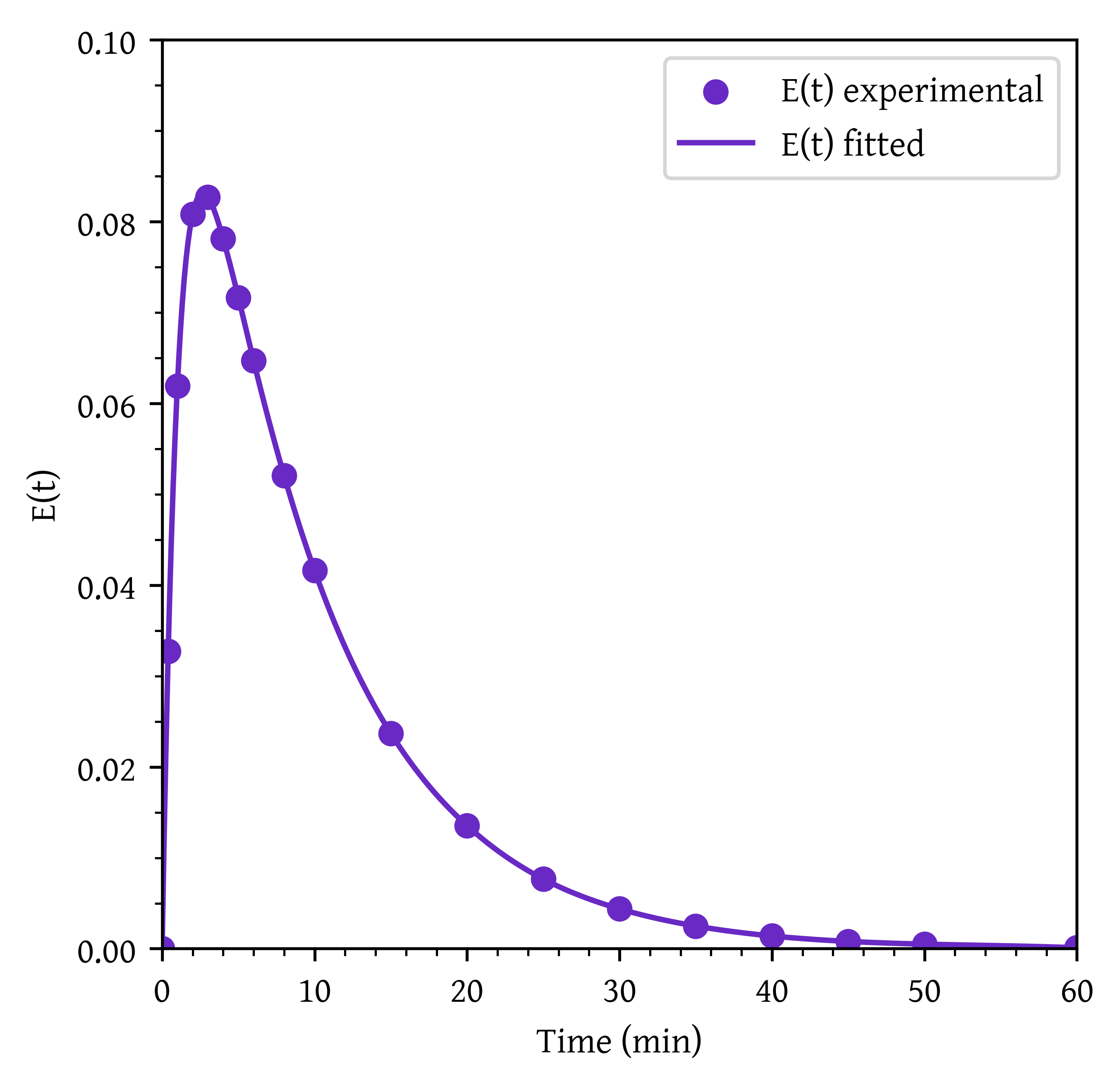
Plot the external-age distribution as a function of time.
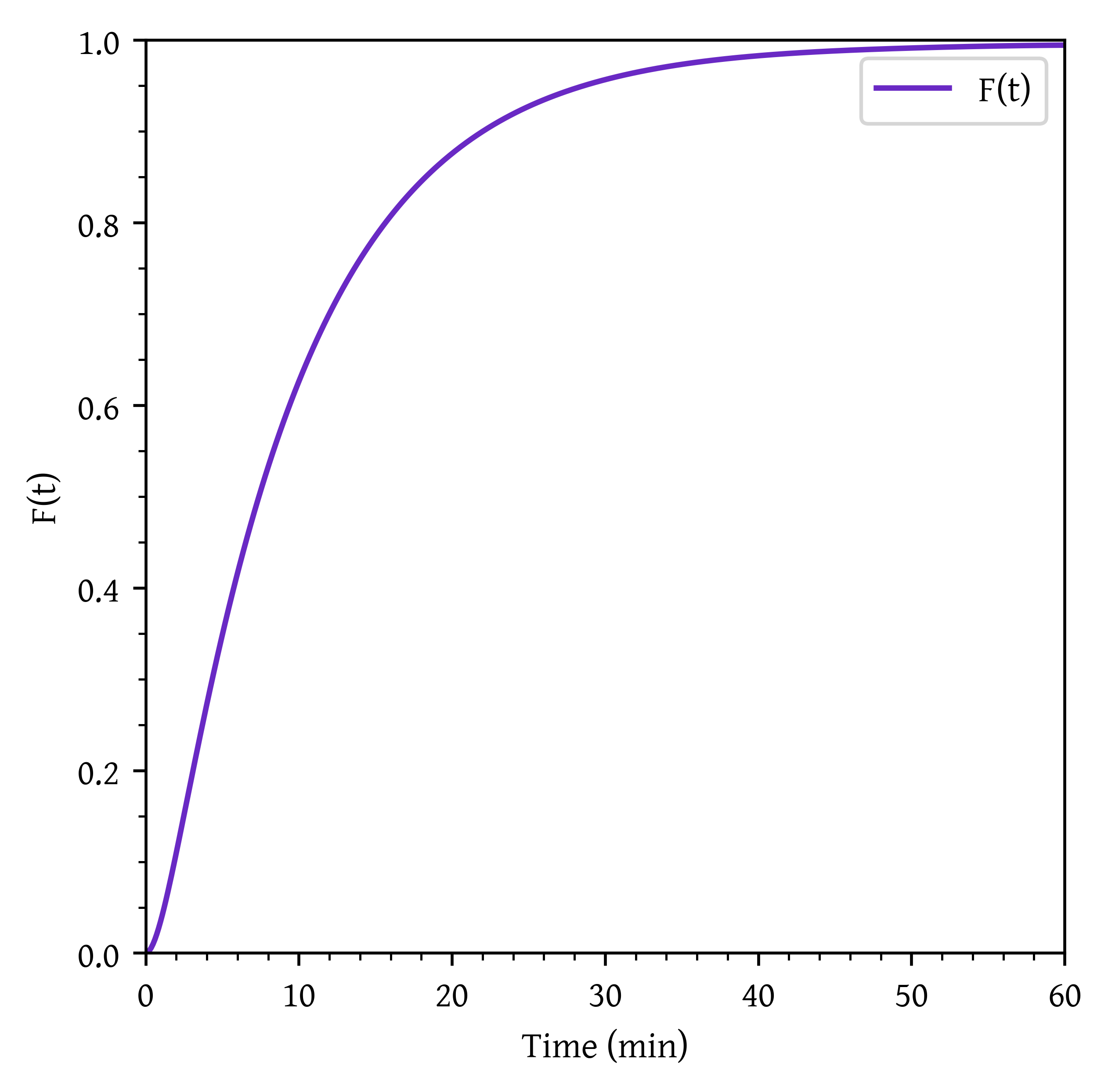
Plot the external-age cumulative distribution as a function of time.
What are the mean residence time and the variance, ?
What fraction of the material spends between 2 and 4 minutes in the reactor?
What fraction of the material spends longer than 6 minutes in the reactor?
What fraction of the material spends less than 3 minutes in the reactor?
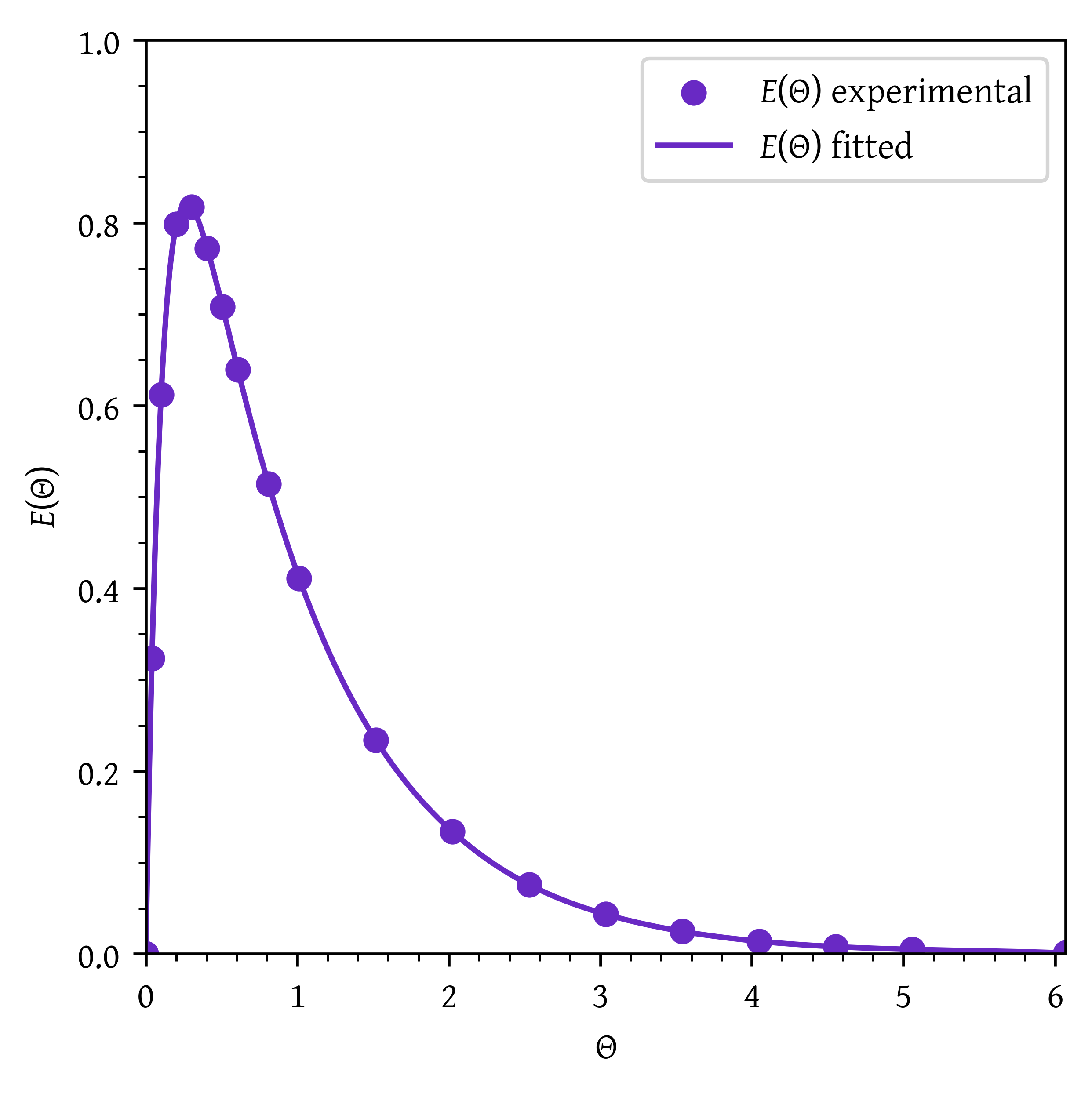
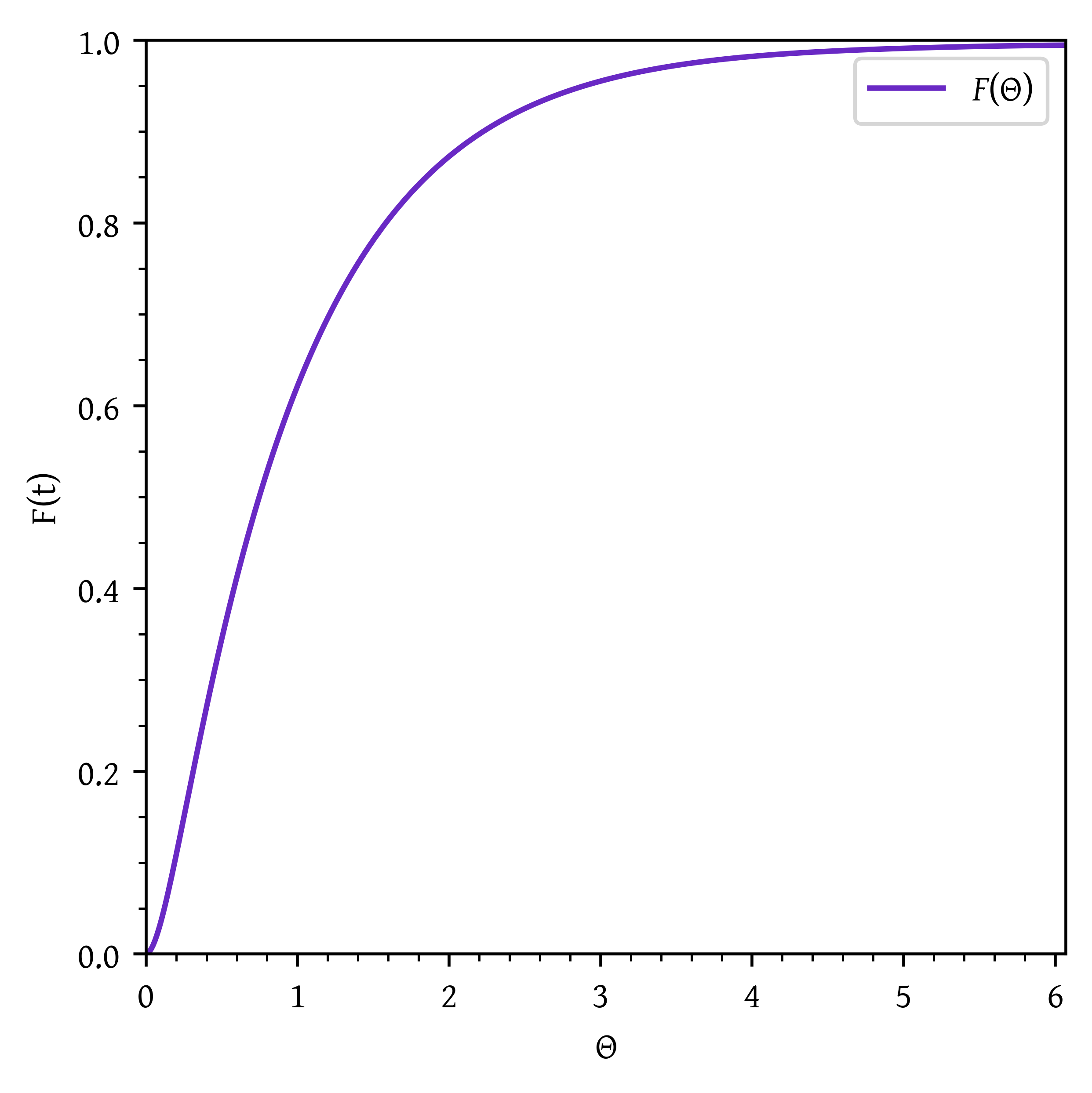
Plot the normalized distributions and as a function of .
What is the reactor volume?
Plot the internal-age distribution as a function of time.
What is the mean internal age ?
Hand written solution, (Accompanying excel file).
import numpy as np
from scipy.integrate import quad
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt
from IPython.display import display, Markdown
# Given data
t = np.array([0, 0.4, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0,
8.0, 10.0, 15, 20, 25, 30, 35, 40, 45, 50, 60])
c = np.array([0, 329, 622, 812, 831, 785, 720, 650,
523, 418, 238, 136, 77, 44, 25, 14, 8, 5, 1]) * 1e-5
# Flow rate
Q = 10 # dm^3/min
# Normalize concentration to calculate E(t)
integral_c = np.trapz(c, t)
et = c / integral_c
# Interpolation functions
et_interp = interp1d(t, et, kind='cubic', fill_value="extrapolate")
# f_interp = lambda t: np.array([quad(et_interp, 0, ti)[0] for ti in t])
# Define cumulative distribution F(t)
def f_interp(t):
return np.array([quad(et_interp, 0, ti, limit=1000)[0] for ti in np.atleast_1d(t)])
# Mean residence time function
tau_func = lambda t: t * et_interp(t)
# Variance function
variance_func = lambda t, tm: (t - tm)**2 * et_interp(t)
# Calculate mean residence time (t_m)
tau, _ = quad(tau_func, 0, np.max(t))
# Calculate variance (σ²)
variance, _ = quad(variance_func, 0, np.max(t), args=(tau,))# Plot E(t) and F(t)
t_plot = np.linspace(0, 60, 500)
et_plot = et_interp(t_plot)
f_plot = f_interp(t_plot)
plt.scatter(t, et, label='E(t) experimental')
plt.plot(t_plot, et_plot, label='E(t) fitted')
plt.xlabel('Time (min)')
plt.ylabel('E(t)')
plt.xlim(np.min(t_plot), np.max(t_plot))
plt.ylim(0,0.1)
plt.legend()
plt.show()plt.plot(t_plot, f_plot, label='F(t)')
plt.xlabel('Time (min)')
plt.ylabel('F(t)')
plt.xlim(np.min(t_plot), np.max(t_plot))
plt.ylim(0,1)
plt.legend()
plt.show()# Calculate specific time fractions
fraction_2_to_4, _ = quad(et_interp, 2, 4)
fraction_above_6, _ = quad(et_interp, 6, np.max(t))
fraction_below_3, _ = quad(et_interp, 0, 3)
# Reactor volume calculation
volume = Q * tauMean Residence Time : 9.88 min.
Variance : 75.69
Specific Time Fractions:
Fraction of material that spends between 2 and 4 minutes: 0.163
Fraction of material that spends longer than 6 minutes: 0.578
Fraction of material that spends less than 3 minutes: 0.193
Reactor Volume: : 98.83
Normalized distrubution:
To calculate normalized RTD, we convert t to as .
The dimensionless RTD function is calculated as .
Normalized cumulative RTD:
theta = t/tau
e_theta = tau * et
e_theta_interp = interp1d(theta, e_theta, kind='cubic', fill_value="extrapolate")
theta_plot = np.linspace(0, theta[-1], 500)
e_theta_plot = e_theta_interp(theta_plot)
plt.scatter(theta, e_theta, label='$E(\\Theta)$ experimental')
plt.plot(theta_plot, e_theta_plot, label='$E(\\Theta)$ fitted')
plt.xlabel('$\\Theta$')
plt.ylabel('$E(\\Theta)$')
plt.xlim(np.min(theta_plot), np.max(theta_plot))
plt.ylim(0,1)
plt.legend()
plt.show()f_theta_interp = lambda t: np.array([quad(e_theta_interp, 0, ti)[0] for ti in t])
f_theta_plot = f_theta_interp(theta_plot)
plt.plot(theta_plot, f_theta_plot, label='$F(\\Theta)$')
plt.xlabel('$\\Theta$')
plt.ylabel('F(t)')
plt.xlim(np.min(theta_plot), np.max(theta_plot))
plt.ylim(0,1)
plt.legend()
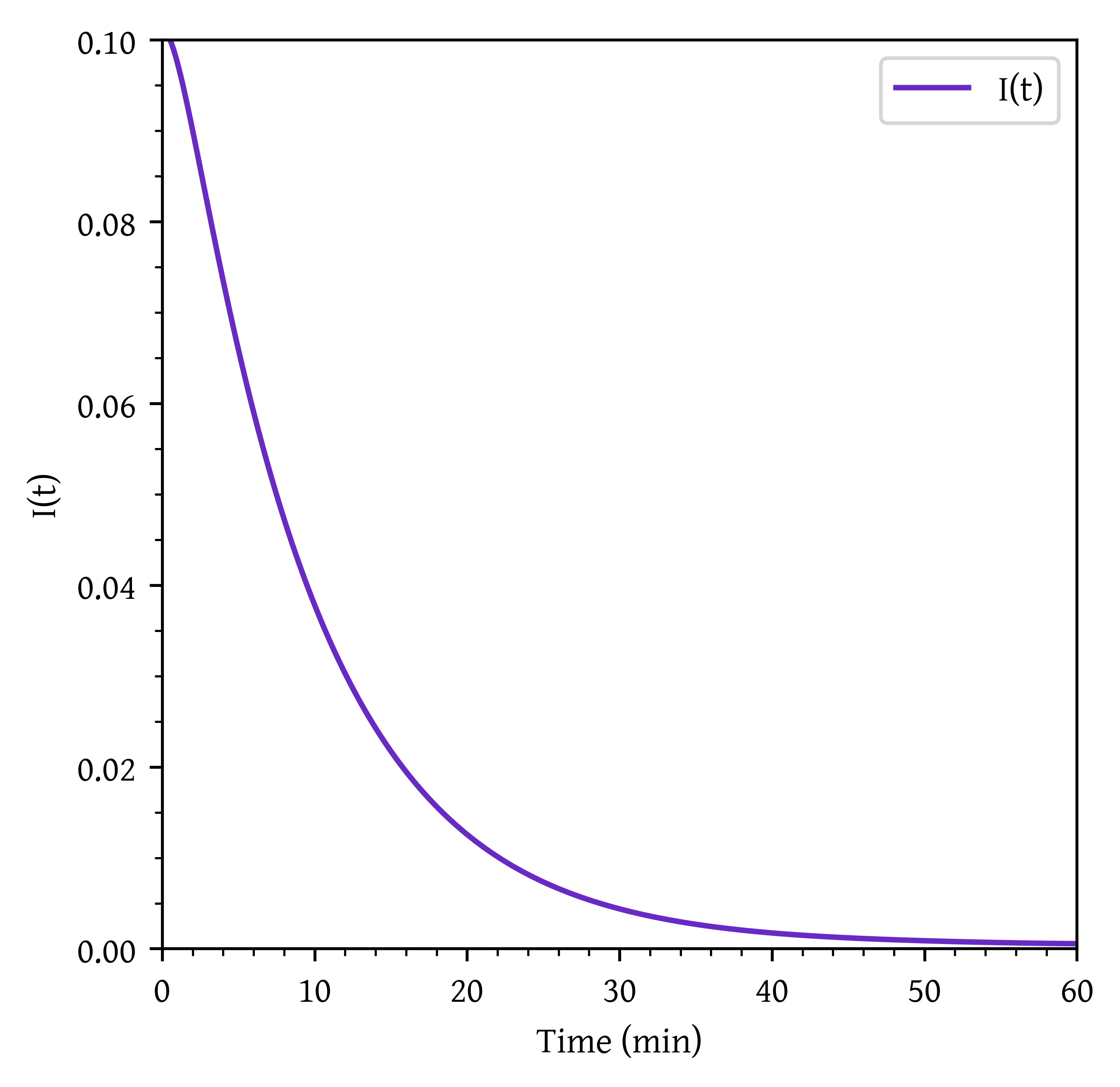
plt.show()Internal age distribution
Mean internal age
internal_age = lambda t, tm: (1/tm) * (1 - f_interp(t))
mean_internal_age, _ = quad(lambda t: internal_age(t, tau), 0, np.max(t))
it_plot = internal_age(t_plot, tau)
plt.plot(t_plot, it_plot, label='I(t)')
plt.xlabel('Time (min)')
plt.ylabel('I(t)')
plt.xlim(np.min(t_plot), np.max(t_plot))
plt.ylim(0,0.1)
plt.legend()
plt.show()Mean Internal age : 1.03 min.
References
Citation
@online{utikar2024,
author = {Utikar, Ranjeet},
title = {Solutions to Workshop 11: {Distribution} of Residence Time},
date = {2024-03-24},
url = {https://cre.smilelab.dev/content/workshops/10-distribution-of-residence-time/solutions.html},
langid = {en}
}