Solutions to workshop 03: Rate law and stoichiometry

Lecture notes for chemical reaction engineering

Try following problems from Fogler 5e(Fogler 2016).

P3-5, P3-10, P3-11, P3-12, P 4-6, P 4-8, P 4-11

We will go through some of these problems in the workshop.

P 3.12

Write the rate law for the following reactions assuming each reaction follows an elementary rate law. Give the units of k_A for each, keeping in mind some are homogeneous and some reactants are heterogeneous.

1. \ce{C2H6 -> C2H4 H2}

2. \ce{C2H4 + 1/2 O2 -> C2H4O}

3. \ce{(CH3)3COOC(CH3)3 <=> C2H6 + 2CH3COCH3}

4. \ce{nC4H10 <=> iC4H10}

5. \ce{ CH3COOC2H5 + C4H9OH <=> CH3COOC4H9 + C2H5OH}

6. \ce{2CH3NH2 <=>[][{cat}] (CH3)2NH + NH3}

7. \ce{ (CH3CO)2O + H2O <=> 2CH3COOH }

Solution

1. -r_A = k C_A

2. -r_A = k C_A C_B^{1/2}

3. -r_A = k \left( C_A -\frac{C_B C_C}{K} \right)

4. -r_A = k \left( C_A -\frac{C_B}{K} \right)

5. -r_A = k \left( C_A C_B -\frac{C_C C_D}{K} \right)

6. -r'_A = k \left( P_A^2 -\frac{P_B P_C}{K} \right)

7. -r_A = k \left( C_A C_B -\frac{C_C^2}{K} \right)

P3-10

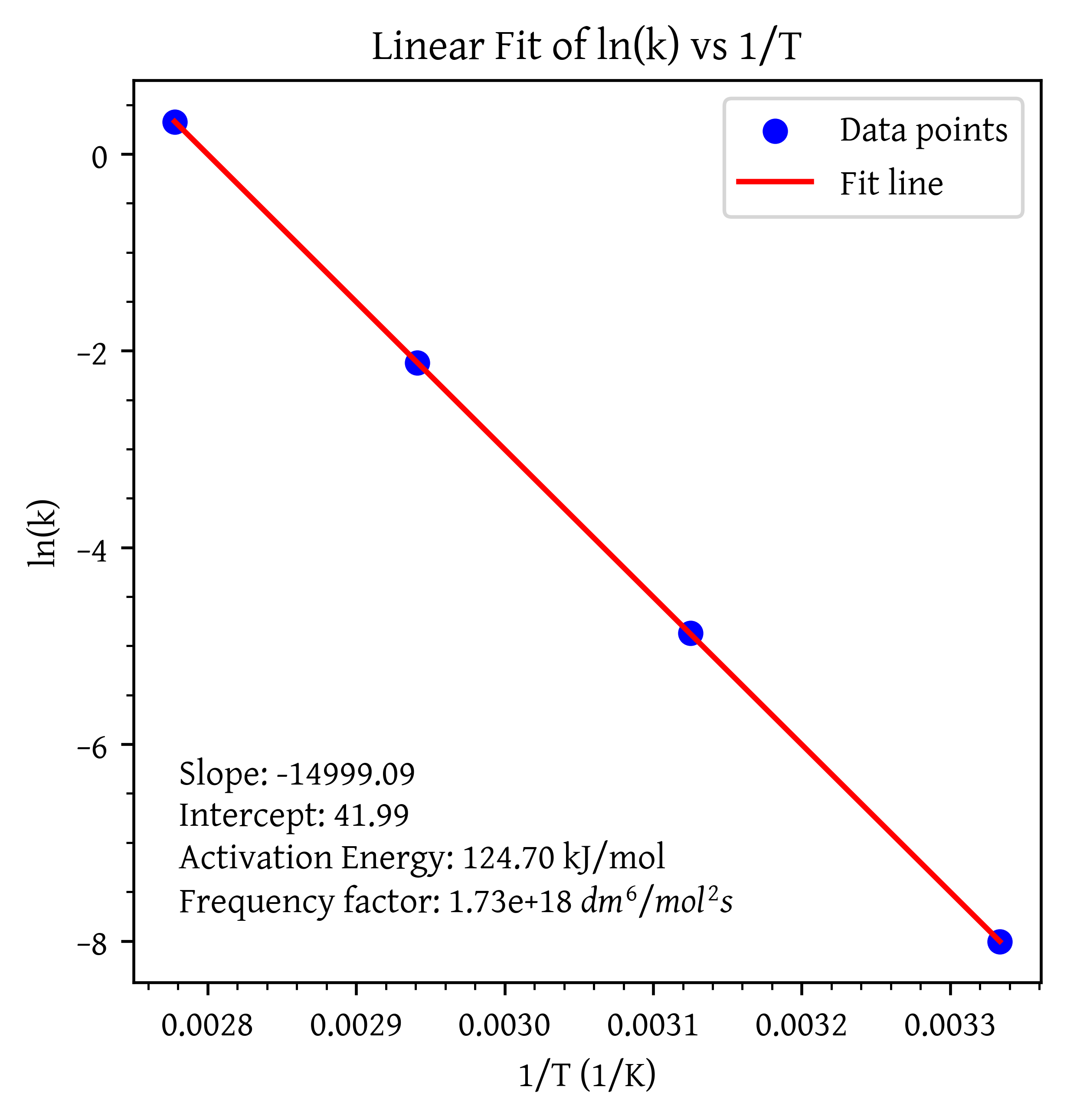
The initial reaction rate for the elementary reaction \ce{2A + B -> 4C} was measured as a function of temperature when the concentration of A was 2 M and that of B was 1.5 M.

–r_A (mol/dm^3 s)	T(K)
0.002	300
0.046	320
0.72	340
8.33	360

1. What is the activation energy?

2. What is the frequency factor?

3. What is the rate constant as a function of temperature using Equation 1 and T_0 = 27 °C as the base case?

   k(T) = k(T_0) exp \left[ \frac{E}{R} \left( \frac{1}{T_0} - \frac{1}{T} \right)\right] \tag{1}

Solution

\ce{2A + B -> 4C}. Elementary reaction. Initial rates given.

For elementary reaction

-r_A = k C_A^2 C_B

k = \frac{-r_A}{C_A^2 C_B}

At the start of reaction:

k = \frac{-r_{A0}}{C_{A0}^2 C_{B0}}

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import linregress

# Data 
r_A = np.array([0.002, 0.046, 0.72, 8.33])
T = np.array([300, 320, 340, 360])

R = 8.314 # J/mol K
C_A0 = 2.0
C_B0 = 1.5

k = r_A/(C_A0**2 * C_B0)

ln_k = np.log(k)
inv_T = 1 / T

slope, intercept, r_value, p_value, std_err = linregress(inv_T, ln_k)
line = slope * inv_T + intercept

activation_energy = -slope*R/1000 # (kJ/mol)
A0 = np.exp(intercept)

# Plot 
plt.scatter(inv_T, ln_k, color='blue', label='Data points')
plt.plot(inv_T, line, color='red', label='Fit line')

# Labels and title
plt.xlabel('1/T (1/K)')
plt.ylabel('ln(k)')
plt.title('Linear Fit of ln(k) vs 1/T')
plt.legend()

slope_text = f'Slope: {slope:.2f}'
intercept_text = f'Intercept: {intercept:.2f}'
e_text = f'Activation Energy: {activation_energy:.2f} kJ/mol'
a0_text = f'Frequency factor: {A0:.2e} $dm^6/mol^2 s$'
plt.annotate(f'{slope_text}\n{intercept_text}\n{e_text}\n{a0_text}', xy=(0.05, 0.25), xycoords='axes fraction', verticalalignment='top')

# Show plot
plt.show()

k = 1.73 \times 10^{18} \exp \left[ \frac{ -15000 } {T} \right]

P 4-8

The gas-phase reaction

\ce{1/2 N2 + 3/2 H2 -> NH3}

is to be carried out isothermally first in a flow reactor. The molar feed is 50% \ce{H2} and 50% \ce{N2} , at a pressure of 16.4 atm and at a temperature of 227 \ ^{\circ}C?.

1. Construct a complete stoichiometric table.

2. Express the concentrations in mol/dm^3 of each for the reacting species as a function of conversion. Evaluate C_{A0}, \delta and \epsilon, and then calculate the concentrations of ammonia and hydrogen when the conversion of \ce{H2} is 60%.

3. Suppose by chance the reaction is elementary with k_{N_2} = 40 \ dm^3 /mol/s. Write the rate of reaction solely as a function of conversion for

   1. a flow reactor, and for

   2. a constant-volume batch reactor.

Solution

Gas phase reaction

\ce{1/2 N2 + 3/2 H2 -> NH3}

y_A = 0.5

y_B = 0.5

P = 16.4 atm

T = 227 ^\circ C = 500 K

1. stoichiometric table

Basis of reaction: \ce{H2}

\ce{H2 + 1/3 N2 -> 2/3 NH3}; \qquad \ce{A + 1/3 B -> 2/3 C}

Species	Entering	Change	Exiting
A	F_{A0}	-F_{A0}X	F_A = F_{A0}(1 - X)
B	F_{B0} = \Theta_B F_{A0}	-F_{A0}X/3	F_A = F_{A0}(\Theta_B - X/3)
C	0	+ (2/3) F_{A0}X	F_C = (2/3) F_{A0} X

_B = 1

2. Conc. in mol/dm^3 as f(X)

\delta = c/a - b/a -1 = 2/3 - 1/3 -1 = -2/3

\epsilon = y_{A0} \delta = 0.5 \delta = -1/3

C_{A0} = 0.2

C_A = \frac{C_{A0}(1-X)}{(1 + \epsilon X)} \cdots \text{Constant P and T}

C_A = \frac{C_{A0}(1-X)}{(1 + X/3)} \rightarrow X = 0.6 \rightarrow C_A = \frac{0.2 (1 - 0.6)}{(1 + 0.6/3)} = 0.1 mol/dm^3

C_C = \frac{2}{3} \frac{C_{A0}(X)}{(1 + \epsilon X)} \rightarrow X = 0.6 \rightarrow C_C = \frac{2}{3} \frac{0.2 \times 0.6}{(1 + 0.6/3)} = 0.1 mol/dm^3

3. -r_A as f(X), k_{N_2} = 40 dm^3/mol s

1. Flow reactor

-r_{N_2} = k_{N_2} C_{N_2}^{1/2} C_{H_2}^{3/2}

-r_{N_2} = 40 \left[ \frac{C_{A0} (\Theta_B - X/3)}{(1 + \epsilon X)} \right]^{1/2} \left[ \frac{C_{A0} (1 - X)}{(1 + \epsilon X)} \right]^{3/2}

-r_{N_2} = 40 C_{A0}^2 \left[ \frac{(1- X)}{(1 - X/3)} \right]^{3/2} = 1.6 \left[ \frac{(1- X)}{(1 - X/3)} \right]^{3/2}

2. For constant volume batch reactor

-r_{N_2} = k_{N_2} C_{N_2}^{1/2} C_{H_2}^{3/2}

-r_{N_2} = 40 C_{A0}^2 (1- X/3)^{1/2} (1 - X)^{3/2} = 1.6 (1- X/3)^{1/2} (1 - X)^{3/2}

P 4-11

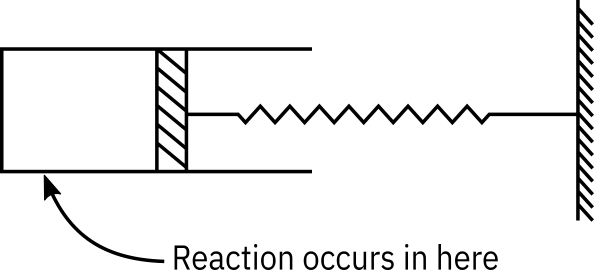
Consider a cylindrical batch reactor that has one end fitted with a frictionless piston attached to a spring (See Figure Figure 1). The reaction

\ce{A + B -> 8 C}

with the rate law

-r_A = k_1 C_A^2 C_B

is taking place in this type of reactor.

Figure 1: Cylindrical batch reactor

1. Write the rate law solely as a function of conversion, numerically evaluating all possible symbols.

2. What is the conversion and rate of reaction when V=0.2 \ ft^3 ?

Additional information:

Equal moles of A and B are present at t_0

Initial volume: 0.15 \ ft^3

Value of k_1 : 1.0 \ (ft^3 /lb mol)^2 \cdot s^{-1}

The spring constant is such that the relationship between the volume of the reactor and pressure within the reactor is

V = (0.1)\ (P) (V in ft^3 , P in atm)

Temperature of system (considered constant): 140 \ ^{\circ}F

Gas constant: 0.73 \ ft^3 atm/lb mol \cdot ^{\circ}R

Solution

1. Rate law as f(X)

y_{A0} = \frac{N_{A0}}{N_{A0} + N_{B0}} = 0.5

\delta = 8 - 1 - 1 = 6

\epsilon = y_{A0} \delta = 3

V = V_0 (1 + \epsilon X) \frac{P_0}{P} \frac{T}{T_0}

P_0 = 10 V_0; P = 10 V

V = \frac{10 V_0^2}{10 V} (1 + \epsilon X)

V^2 = V_0^2 (1 + \epsilon X)

N_A = N_{A0}(1 - X); N_B = N_{A0} (\Theta_B - X)

\Theta_B = \frac{N_{B0}}{N_{A0}} = 1

-r_A = k C_A^2 C_B = \frac{k N_A^2 N_B}{V^2} = \frac{k N_{A0}^3 (1-X)^3}{V_0^3 (1 + \epsilon X)^3/2}

\frac{N_{A0}}{V_0} = \frac{y_{A0} P}{RT}

\therefore -r_A = k \left( \frac{y_{A0} P_0}{RT} \right)^3 \left( \frac{(1-X)}{(1 + \epsilon X)^{1/2}} \right)^3

-r_A = 5.02 \times 10^{-9} \left( \frac{(1-X)}{(1 + \epsilon X)^{1/2}} \right)^3

2. X and -r_A at V = 0.2 ft^3

V^2 = V_0^2 (1 + \epsilon X)

(0.2)^2 = (0.15)^2 (1 + 3 X) \Rightarrow X = 0.259

-r_A = 8.623 \times 10^{-10} lbmol/ft^3 s

References

Fogler, H. Scott. 2016. Elements of Chemical Reaction Engineering. Fifth edition. Boston: Prentice Hall.