Workshop 02 Solution: Conversion and reactor sizing
Lecture notes for chemical reaction engineering
Problem 1
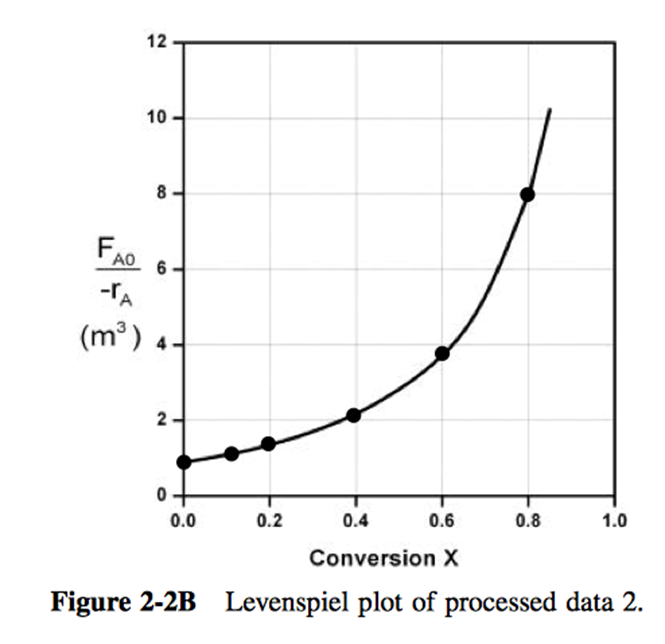
P2-3: You have two CSTRs and two PFRs, each with a volume of . Use Figure 1 to calculate the conversion for each of the reactors in the following arrangements.
- Two CSTRs in series.
- Two PFRs in series.
- Two CSTRs in parallel with the feed, , divided equally between the two reactors.
- Two PFRs in parallel with the feed divided equally between the two reactors.
- A CSTR and a PFR in parallel with the flow equally divided. Calculate the overall conversion,
with
- A PFR followed by a CSTR.
- A CSTR followed by a PFR.
- A PFR followed by two CSTRs. Is this arrangement a good arrangement or is there a better one?
Solution:
To read the CSV file use the genfromtxt function from numpy
import numpy as np
p1_expt_file = './workshop-02-problem-1-data.csv'
p1_expt_data = np.genfromtxt(p1_expt_file,
delimiter=',',
dtype=[('x', float),
('fa0_by_ra', float)],
skip_header=1)To interpolate the data, use CubicSpline function from scipy.interpolate.
import scipy.interpolate as interpolate
p1_interp = interpolate.CubicSpline(p1_expt_data['x'],
p1_expt_data_data['fa0_by_ra'])Data plotting using matplotlib.pyplot
import matplotlib.pyplot as plt
fig,ax = plt.subplots()
ax.scatter(p1_expt_data['x'],
p1_expt_data['fa0_by_ra'],
marker='s',
color='red')
ax.set_xlabel('Conversion X')
ax.set_ylabel('$\\frac{F_{A0}}{-r_A} (m^3)$')
# Setting x and y axis limits
ax.set_xlim(0, 1)
ax.set_ylim(0, 12)
plt.show()Add fit line to the plot
x_interp =np.linspace(0,1,100)
ax.plot(x_interp, p1_interp(x_interp), color='grey')Add rectangle to the plot
# Adds rectangle from (0,0) with a width of x1 and height of y1
rectangle = plt.Rectangle((0, 0), x1, y1, color='skyblue', alpha=0.4)
ax.add_patch(rectangle)Color area under the curve
Fill the area under the curve between x1 and x2
x_fill = np.linspace(x1, x2, 100)
y_fill = p1_interp(x_fill)
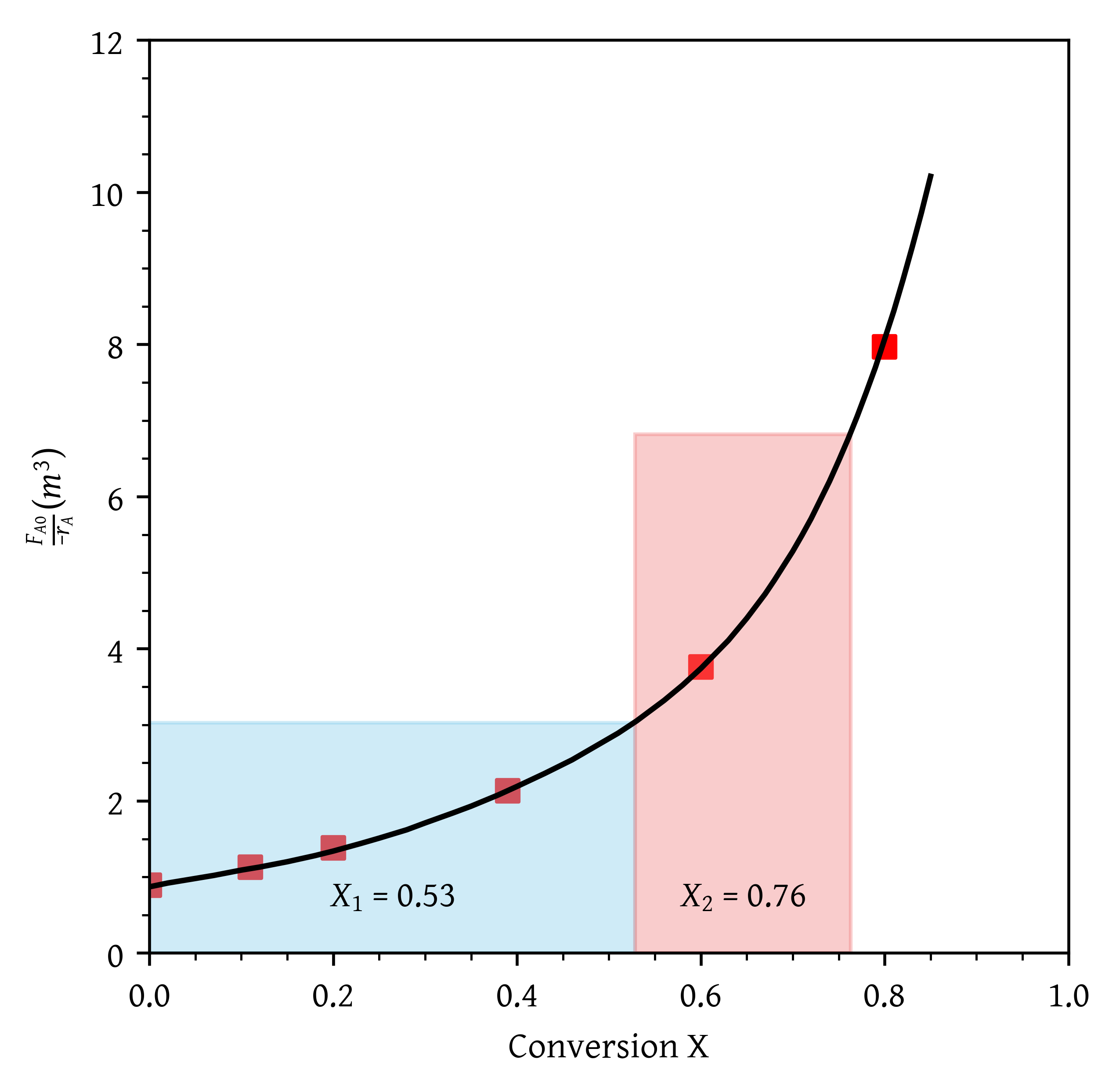
ax.fill_between(x_fill, y_fill, color='skyblue', alpha=0.4)- Two CSTRs in series (Figure 3).
- Two PFRs in series (Figure 4).
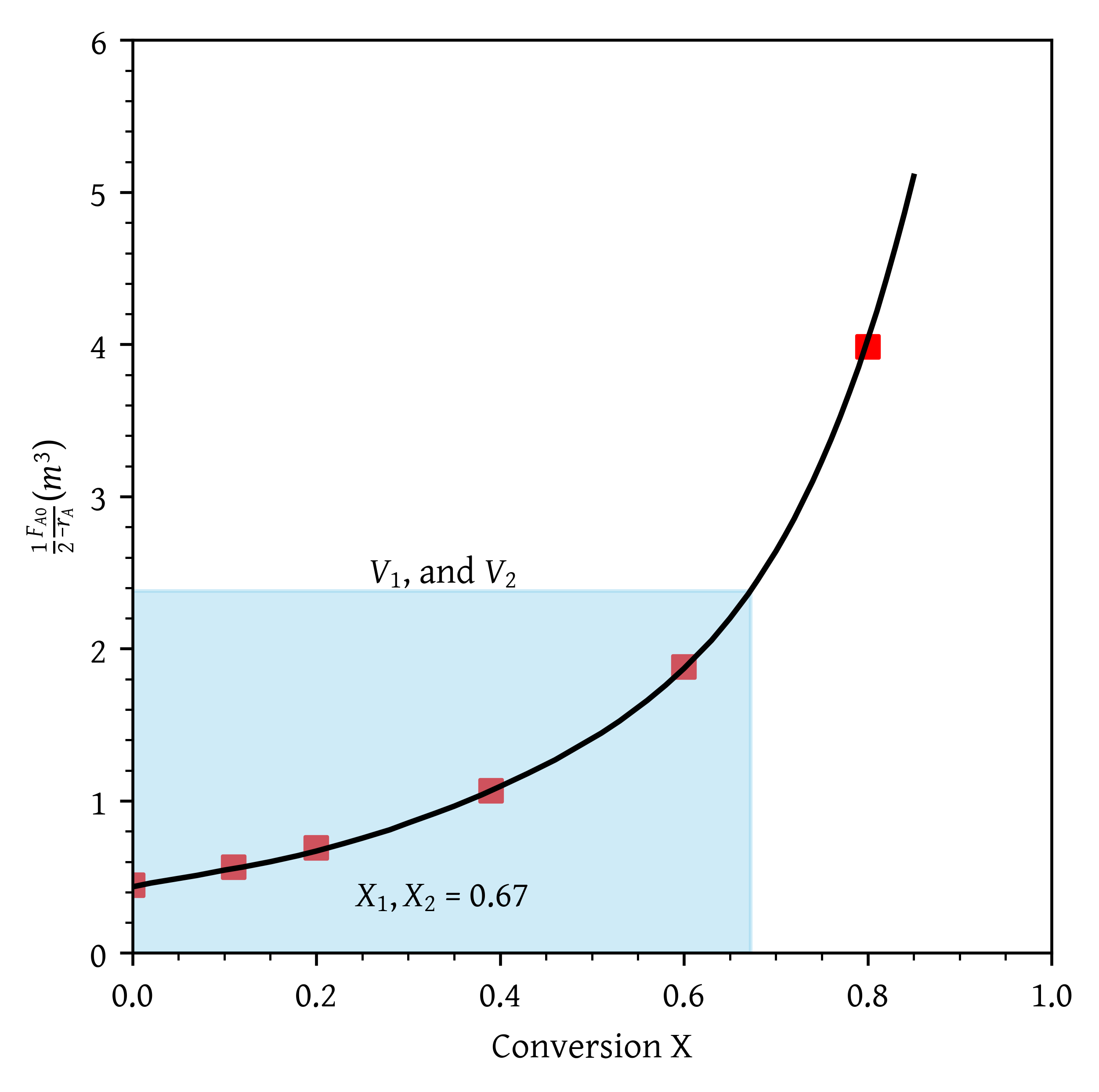
- Two CSTRs in parallel with the feed, , divided equally between the two reactors (Figure 5).
- Two PFRs in parallel with the feed divided equally between the two reactors (Figure 6).
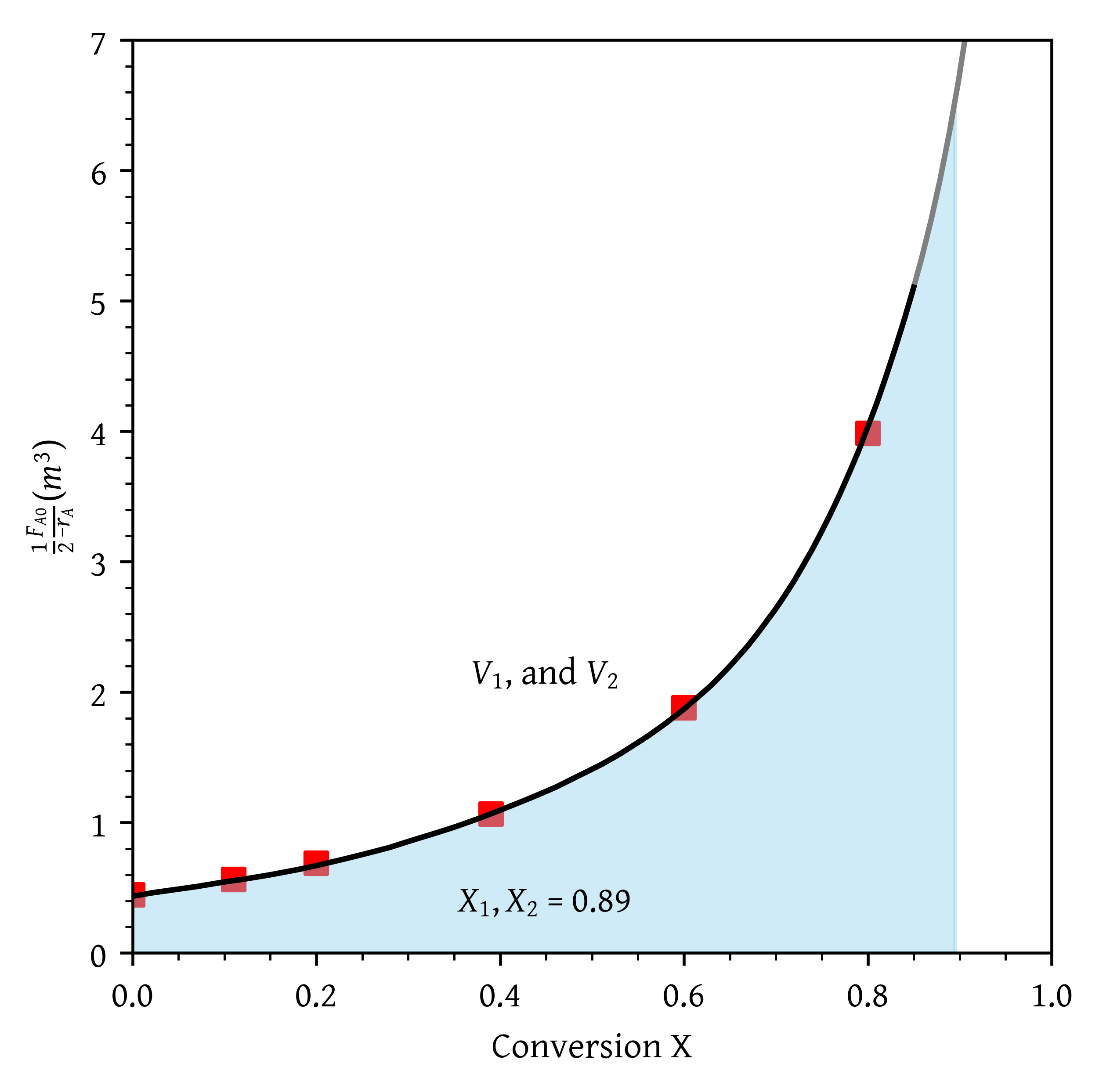
- A CSTR and a PFR in parallel with the flow equally divided. Calculate the overall conversion, (Figure 7)
- A PFR followed by a CSTR (Figure 8).
- A CSTR followed by a PFR (Figure 9).
- A PFR followed by two CSTRs (Figure 10). Is this arrangement a good arrangement or is there a better one?
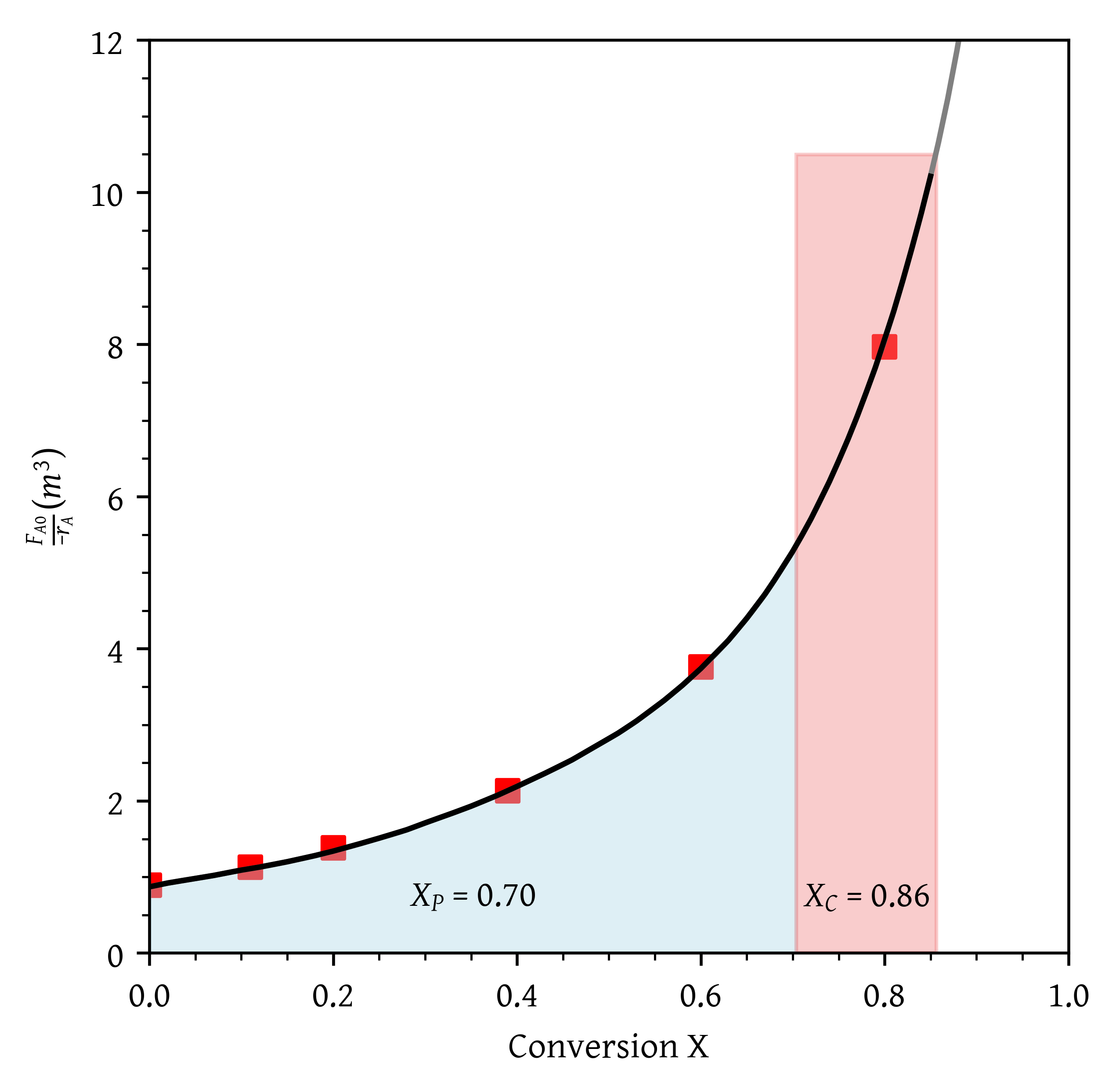
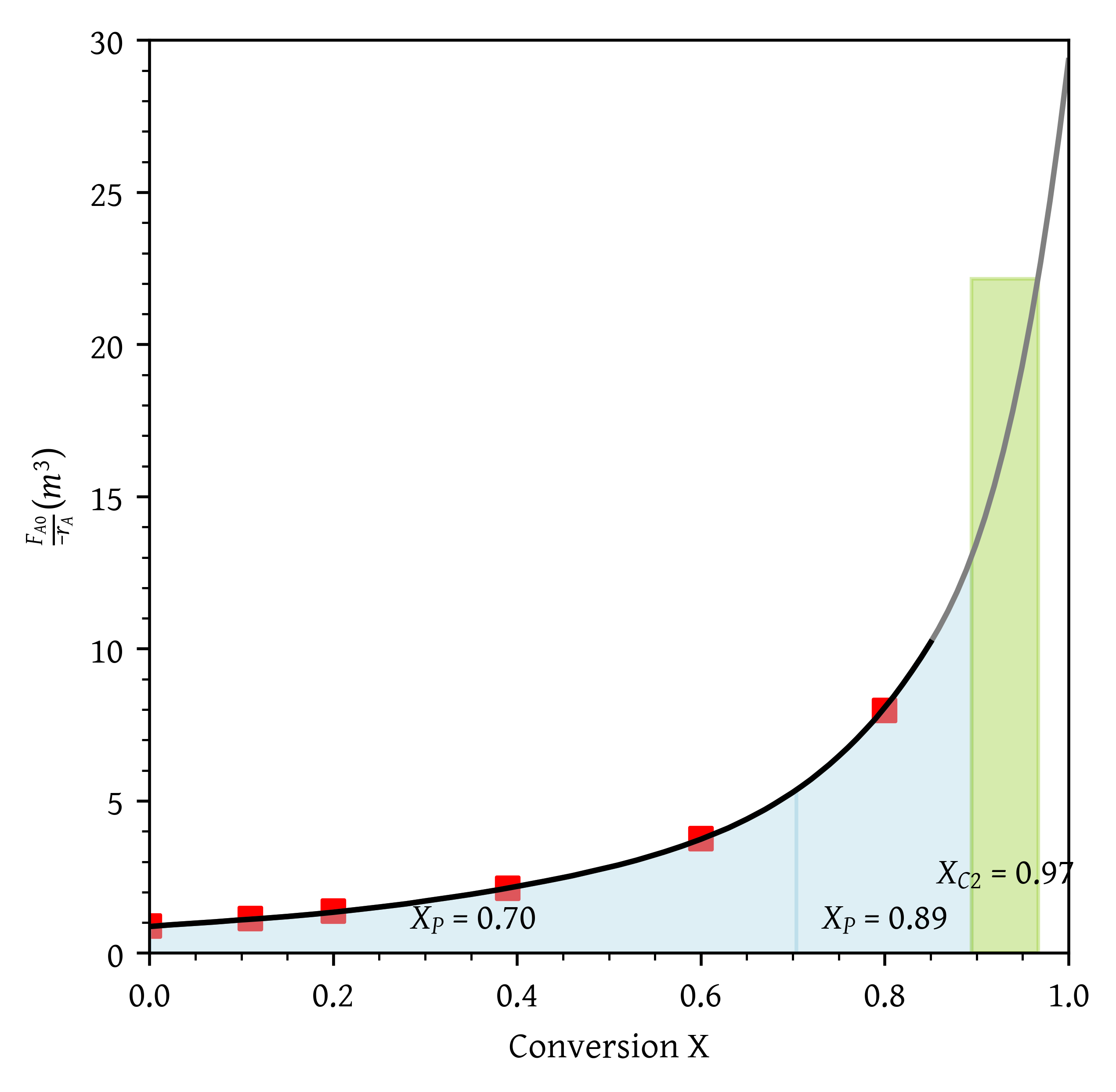
Two CSTRs followed by a PFR (Figure 11) yield final conversion of = 0.92.
Two PFRs followed by a CSTR (Figure 12) yield final conversion of = 0.97.
Problem 2
P2-4: The exothermic reaction of stillbene (A) to form the economically important trospophene (B) and methane (C), i.e.,
was carried out adiabatically and the following data recorded:
The entering molar flow rate of A was .
- What are the PFR and CSTR volumes necessary to achieve 40% conversion?
- Over what range of conversions would the CSTR and PFR reactor volumes be identical?
- What is the maximum conversion that can be achieved in a CSTR?
- What conversion can be achieved if a PFR is followed in series by a CSTR?
- What conversion can be achieved if a CSTR is followed in a series by a PFR?
- Plot the conversion and rate of reaction as a function of PFR reactor volume up to a volume of .
Solution:
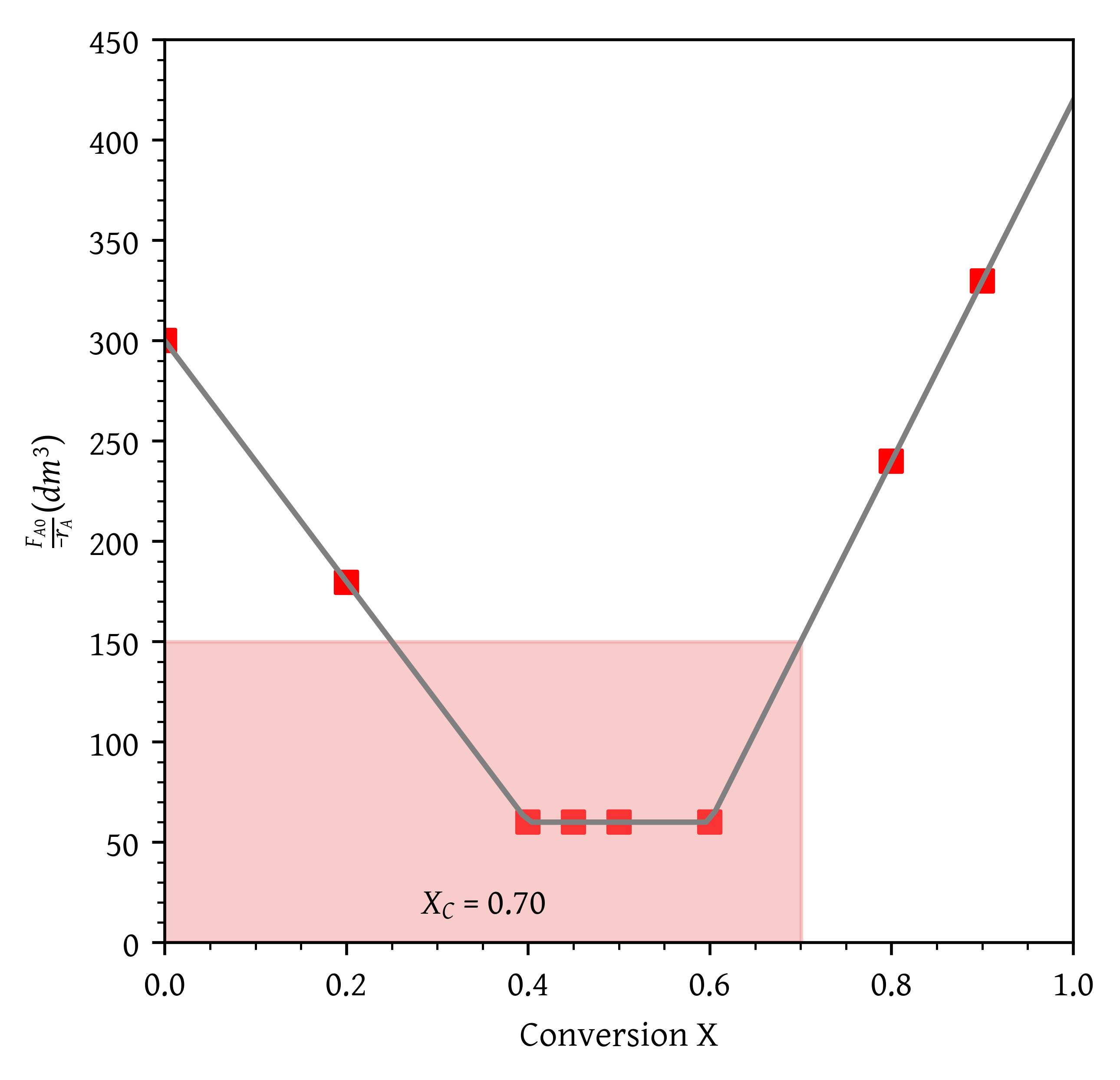
The rate data () is given. We need . Dividing by we get:
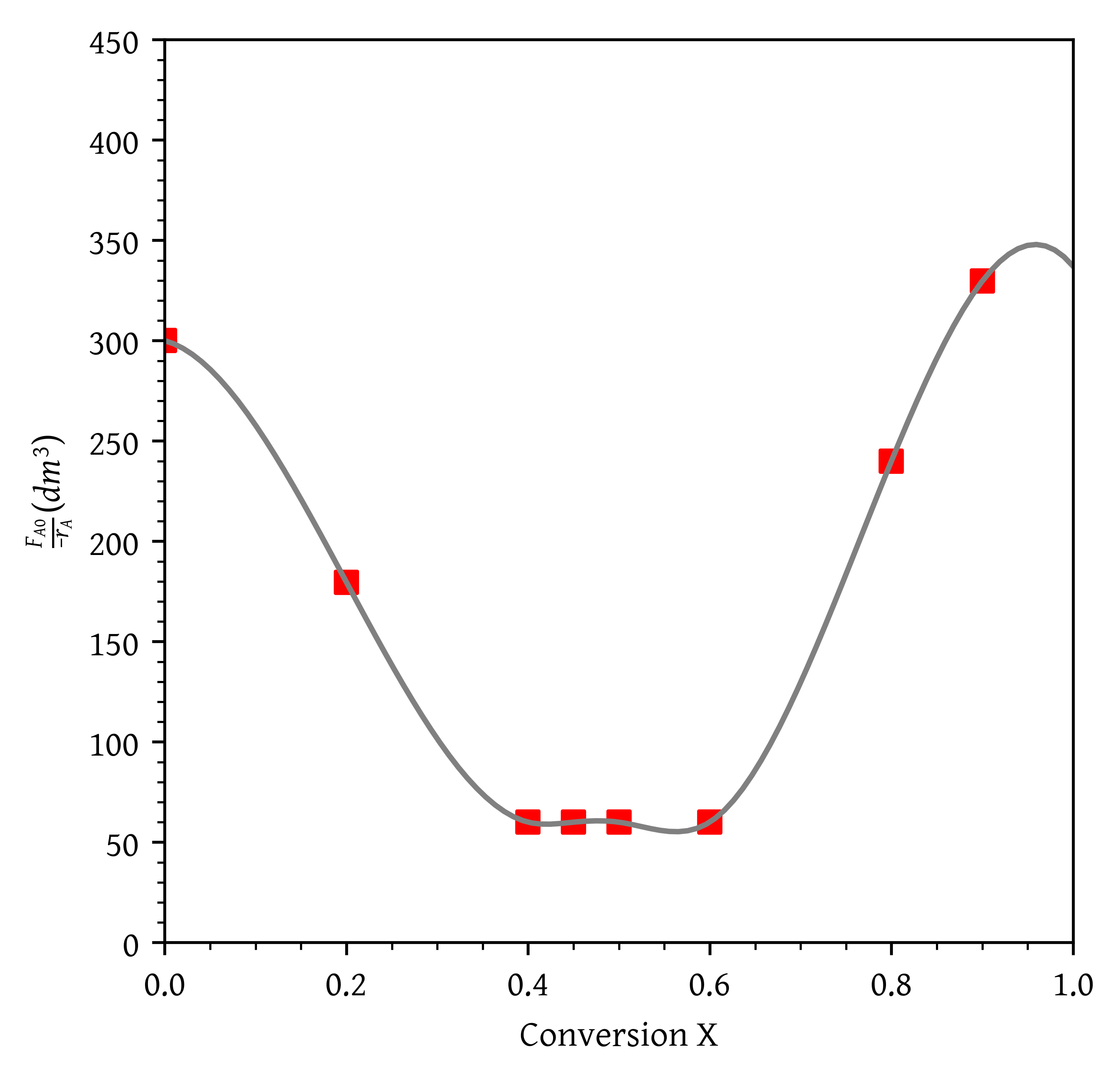
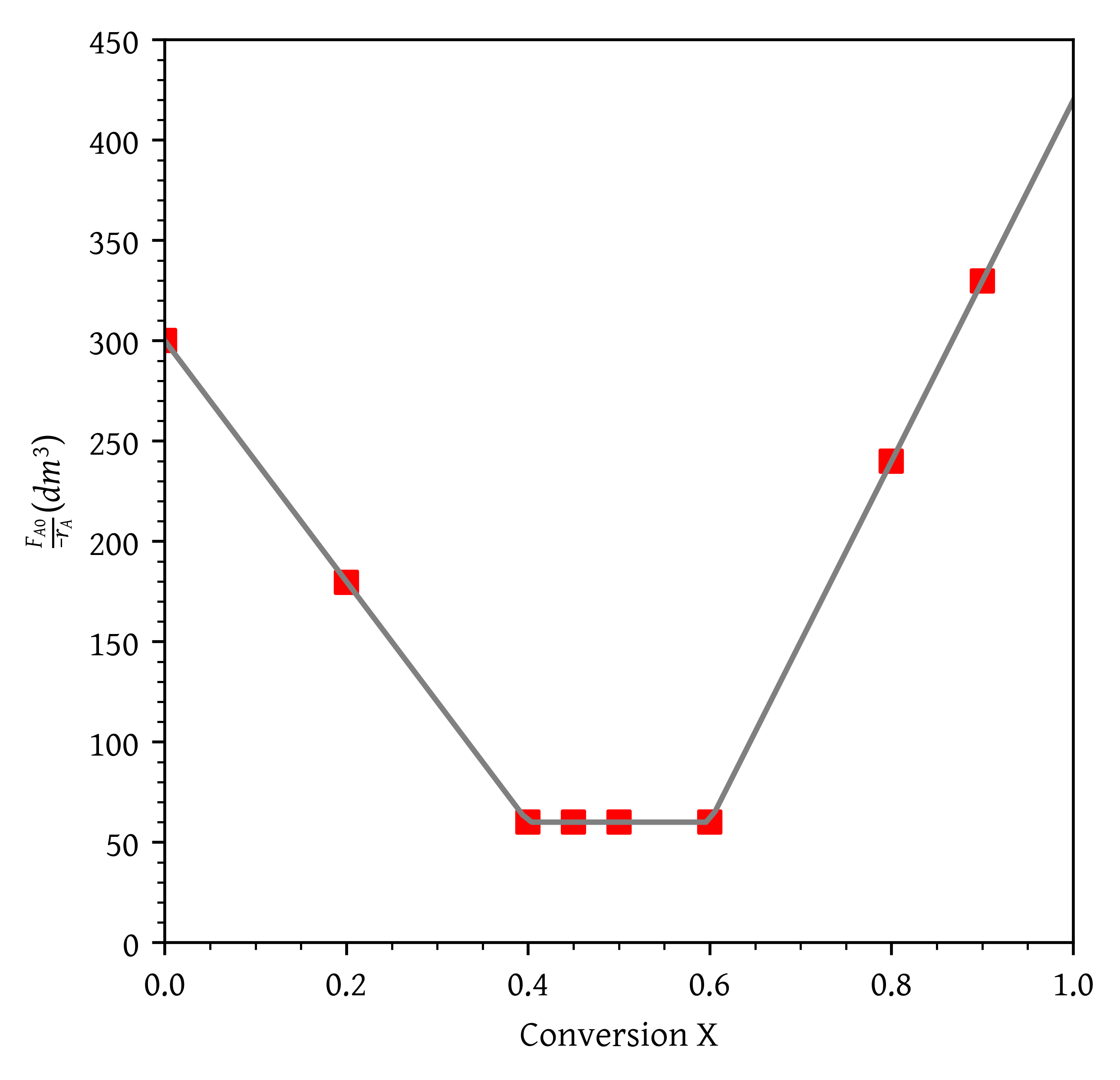
Trying to fit a single cubic spline or a polynomial doesn’t work well due to the nature of the data (Figure 13). The data consists of three liniear segments. Therefore, we fit a piecewise linear function using numpy.piecewise. We also use lambda functions to define the linear segments.
def piecewise_linear_fit(x, x0, y0, k1, k2, k3):
"""
Piecewise linear function defined by slopes and a constant part.
x0, y0: Coordinates of the piecewise function's bending points.
k1, k2, k3: Slopes of the first, second, and third parts.
Note that in this problem,
k1 = -600.0
k2 = 0
k3 = 898.9010989010986
x0 = [0.4, 0.6]
y0 = [60.0, 60.0]
We can call this function as
piecewise_linear_fit(x, *args)
args = ([0.4, 0.6], [60.0, 60.0], -600.0, 0, 898.9010989010986)
"""
return np.piecewise(x,
[x < x0[0], (x >= x0[0]) & (x <= x0[1]), x > x0[1]],
[lambda x: k1*x + y0[0] - k1*x0[0],
lambda x: y0[1],
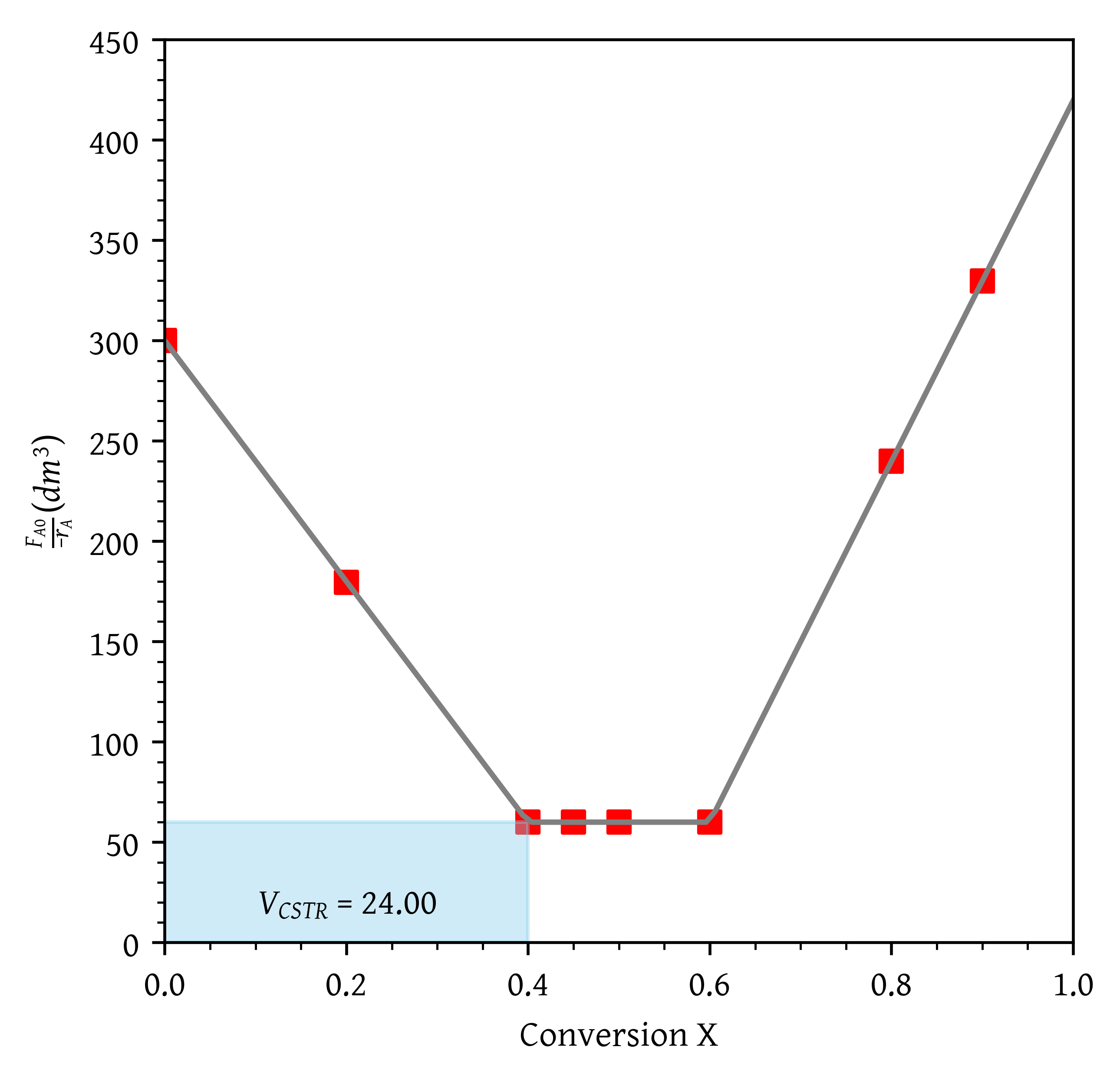
lambda x: k3*x + y0[1] - k3*x0[1]])- What are the PFR and CSTR volumes necessary to achieve 40% conversion?
From @fig-problem-2a, $V_{CSTR}$ = 24\.00 $dm^3$.Over what range of conversions would the CSTR and PFR reactor volumes be identical?
As the slope of line is 0 between 0.4 and 0.6, the CSTR and PFR volumes over this range would be identical.
What is the maximum conversion that can be achieved in a CSTR?
From Figure 16, = 0.70.
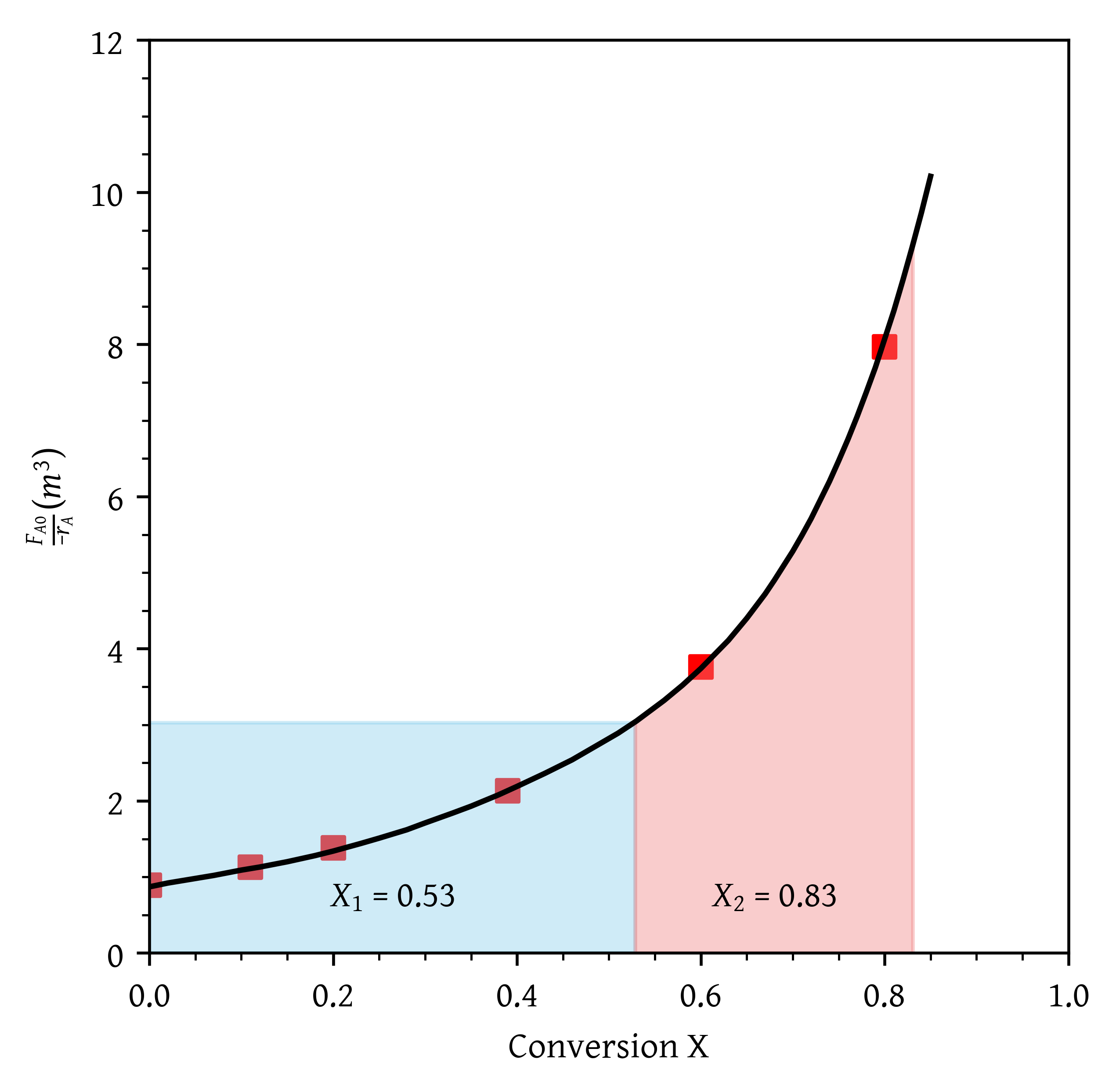
- What conversion can be achieved if a PFR is followed in series by a CSTR?
From Figure 17, = 0.40 and = 0.64.
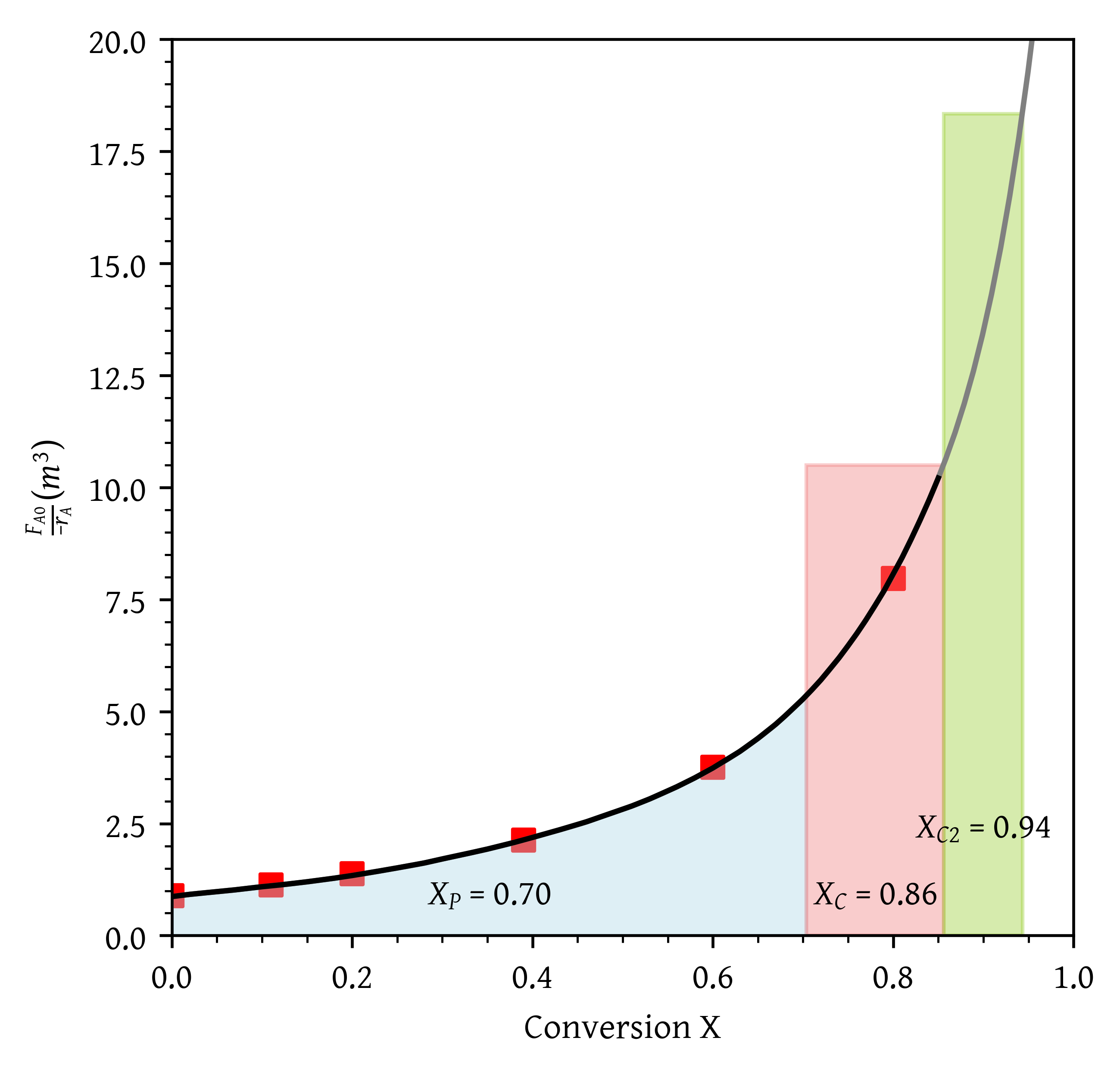
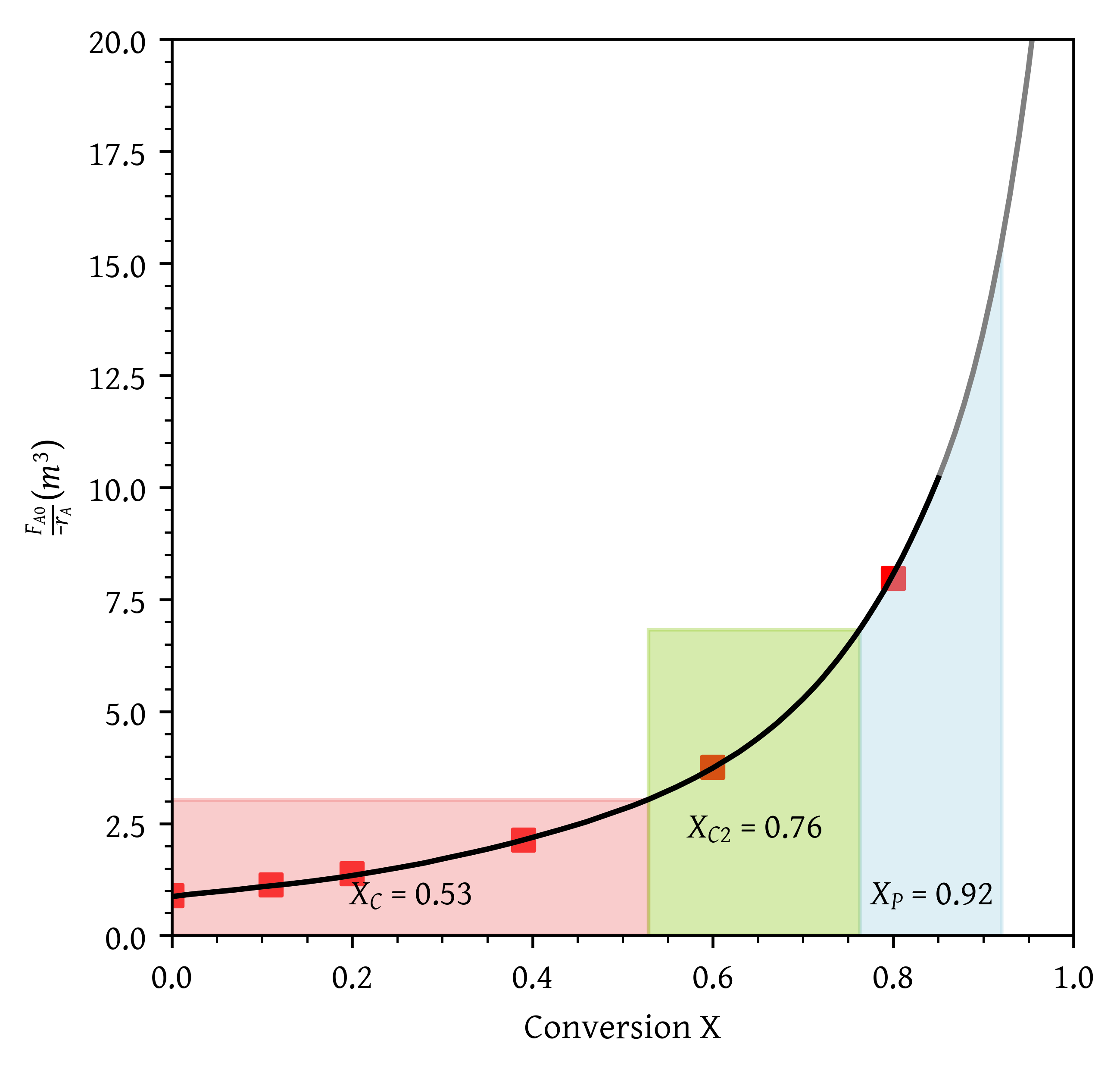
- What conversion can be achieved if a CSTR is followed in a series by a PFR?
From Figure 18, = 0.40 and = 0.91.
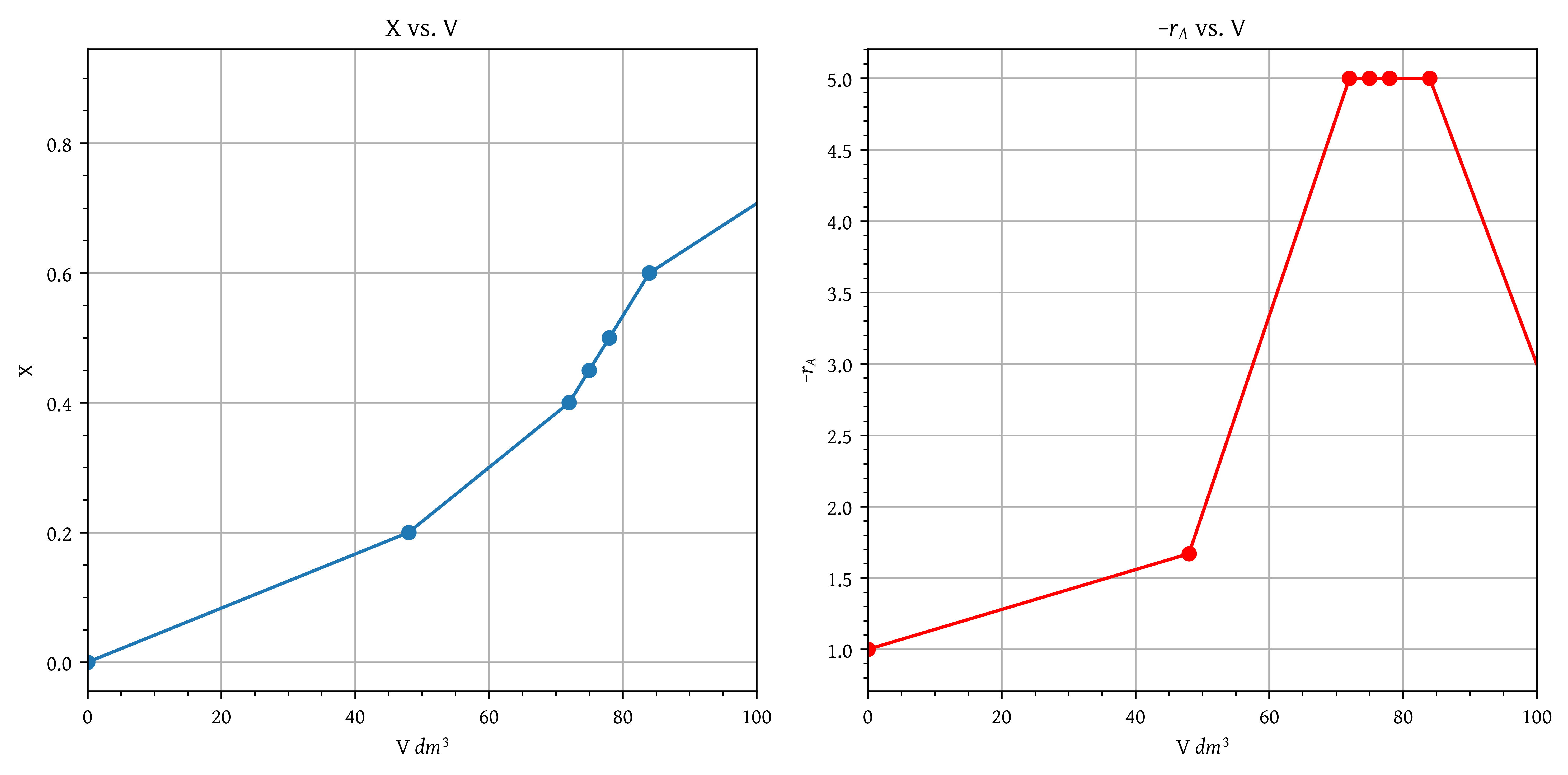
- Plot the conversion and rate of reaction as a function of PFR reactor volume up to a volume of .
To create this plot (Figure 19), we will need to calculate the volume first for all as
This data is given in Table 3
Problem 3
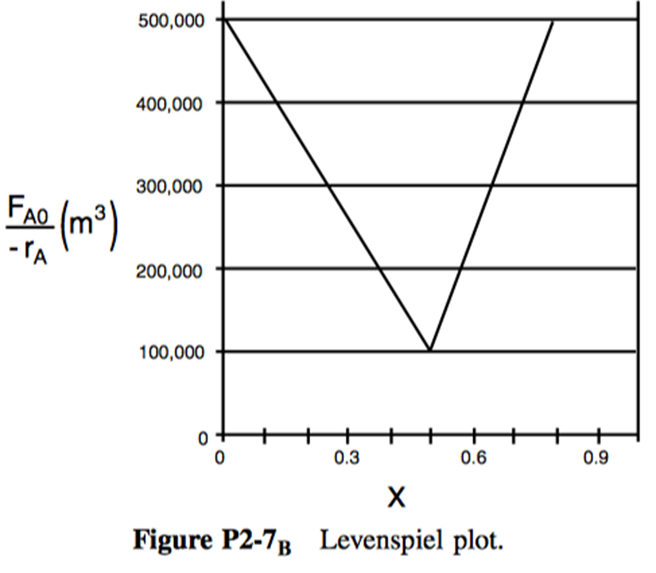
P2-7: The adiabatic exothermic irreversible gas-phase reaction
is to be carried out in a flow reactor for an equimolar feed of A and B. A Levenspiel plot for this reaction is shown in Figure 20 .
- What PFR volume is necessary to achieve 50% conversion?
- What CSTR volume is necessary to achieve 50% conversion?
- What is the volume of a second CSTR added in series to the first CSTR (Part b) necessary to achieve an overall conversion of 80%?
- What PFR volume must be added to the first CSTR (Part b) to raise the conversion to 80%?
- What conversion can be achieved in a CSTR? In a PFR?
- Think critically to critique the answers (numbers) to this problem.
Solution:
Problem 4
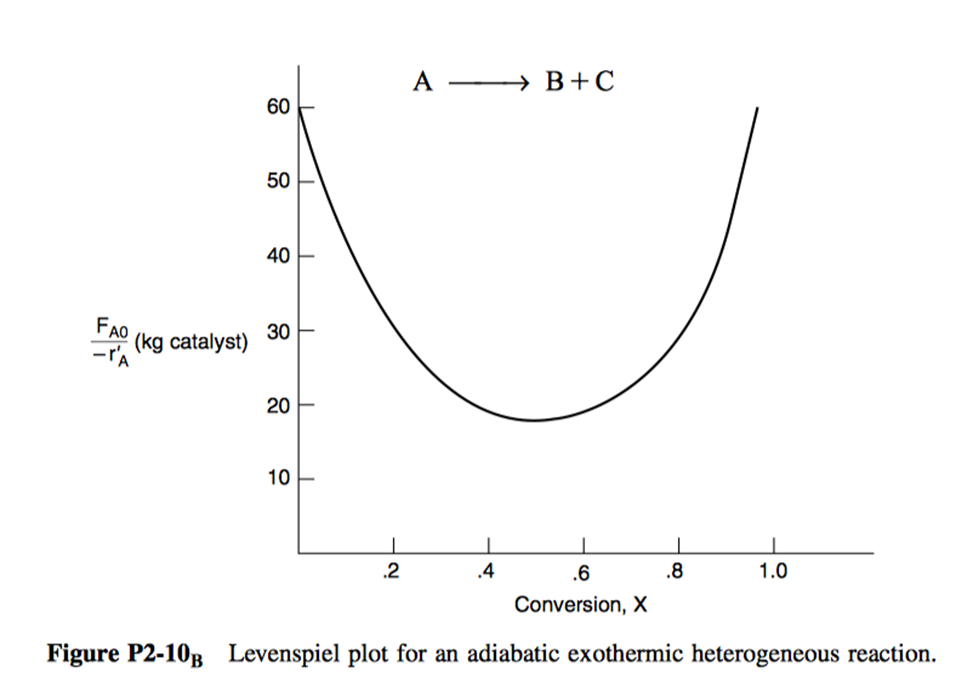
P2.10: The curve shown in Figure 21 is typical of a gas-solid catalytic exothermic reaction carried out adiabatically.
- Assuming that you have a fluidized CSTR and a PBR containing equal weights of catalyst, how should they be arranged for this adiabatic reaction? Use the smallest amount of catalyst weight to achieve 80% conversion of A.
- What is the catalyst weight necessary to achieve 80% conversion in a fluidized CSTR?
- What fluidized CSTR weight is necessary to achieve 40% conversion?
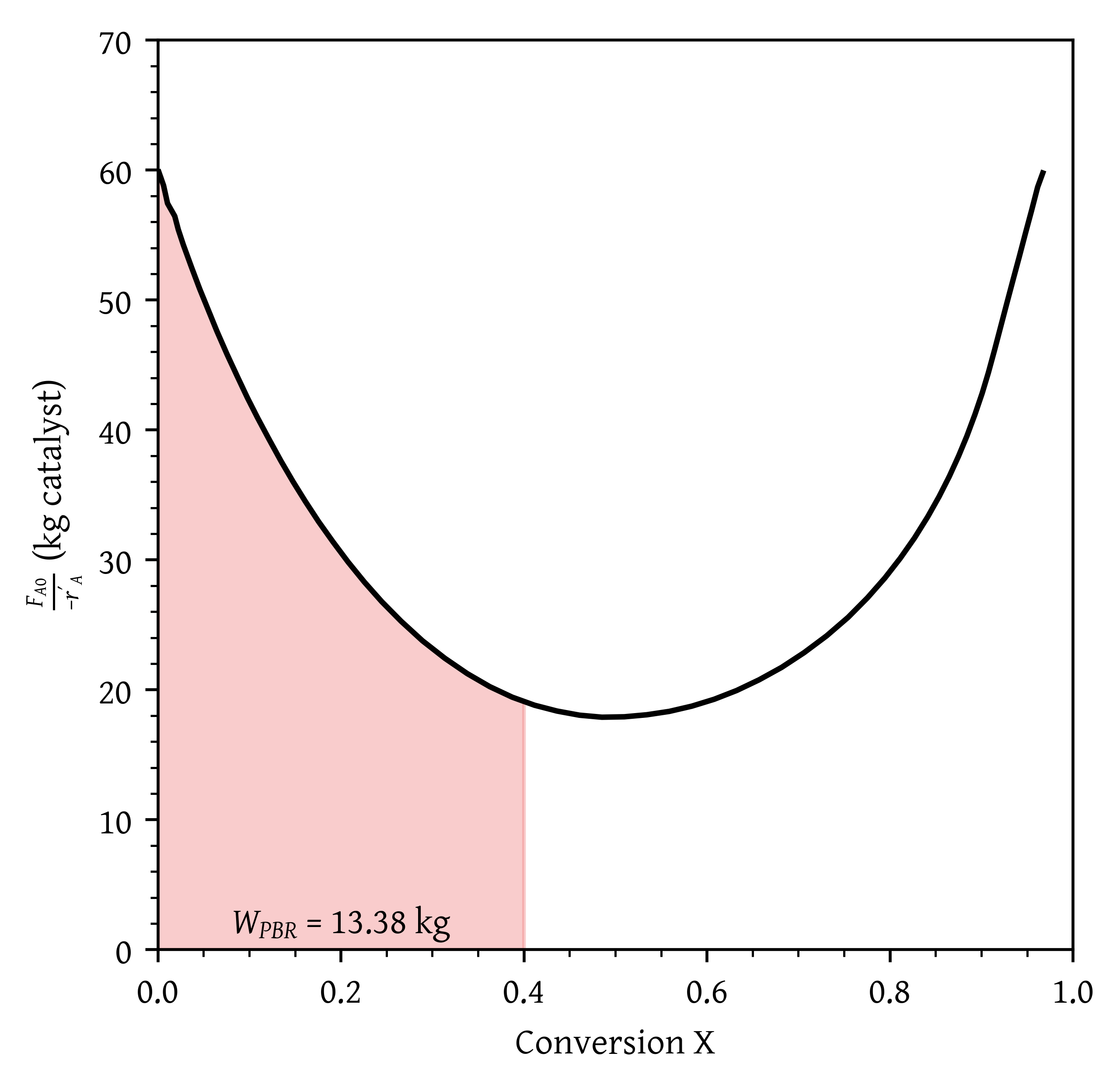
- What PBR weight is necessary to achieve 80% conversion?
- What PBR weight is necessary to achieve 40% conversion?
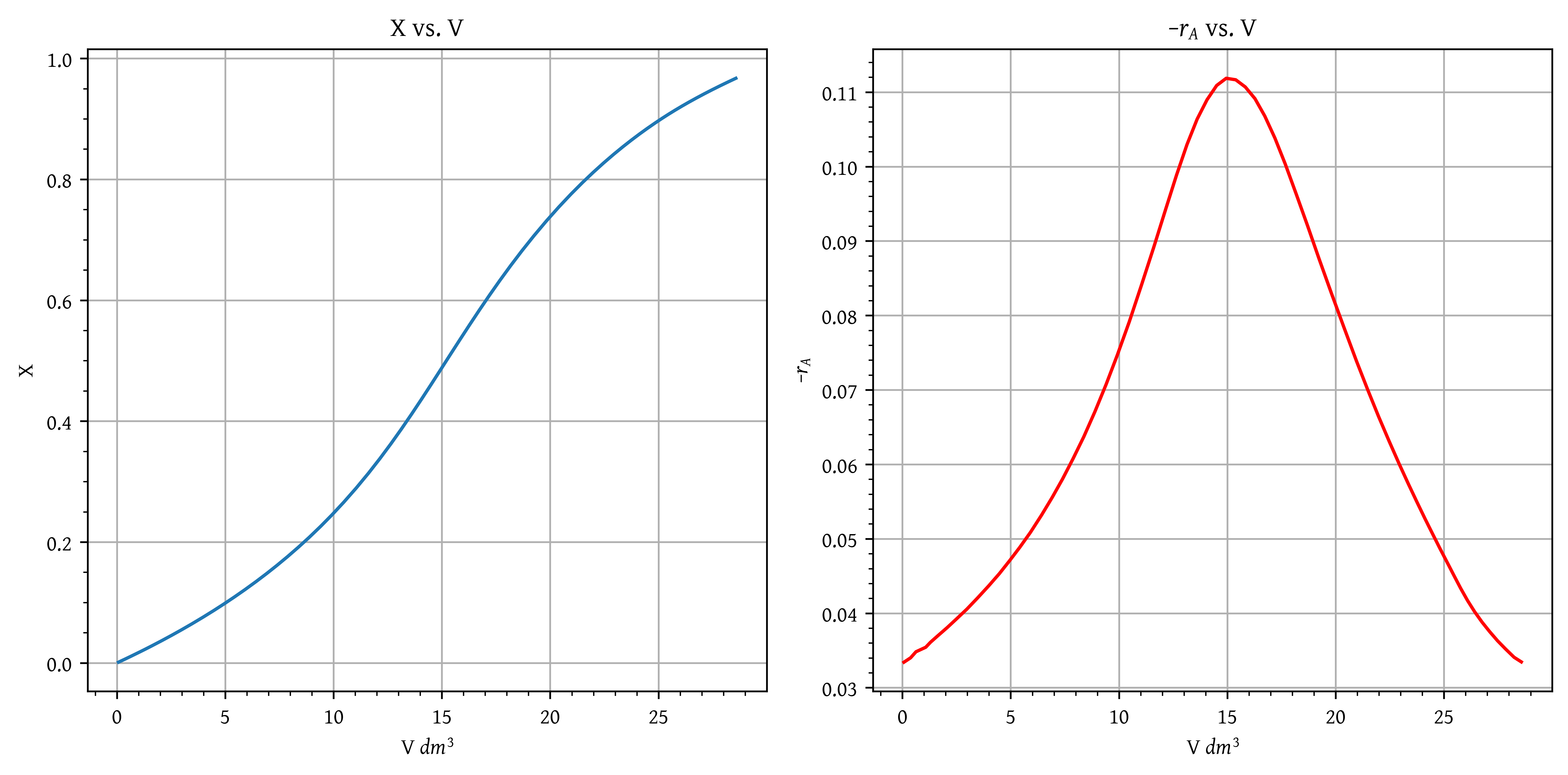
- Plot the rate of reaction and conversion as a function of PBR catalyst weight, W.
Additional information: FA0 = 2 mol/s.
Solution:
Digitized graph: (Figure 22)
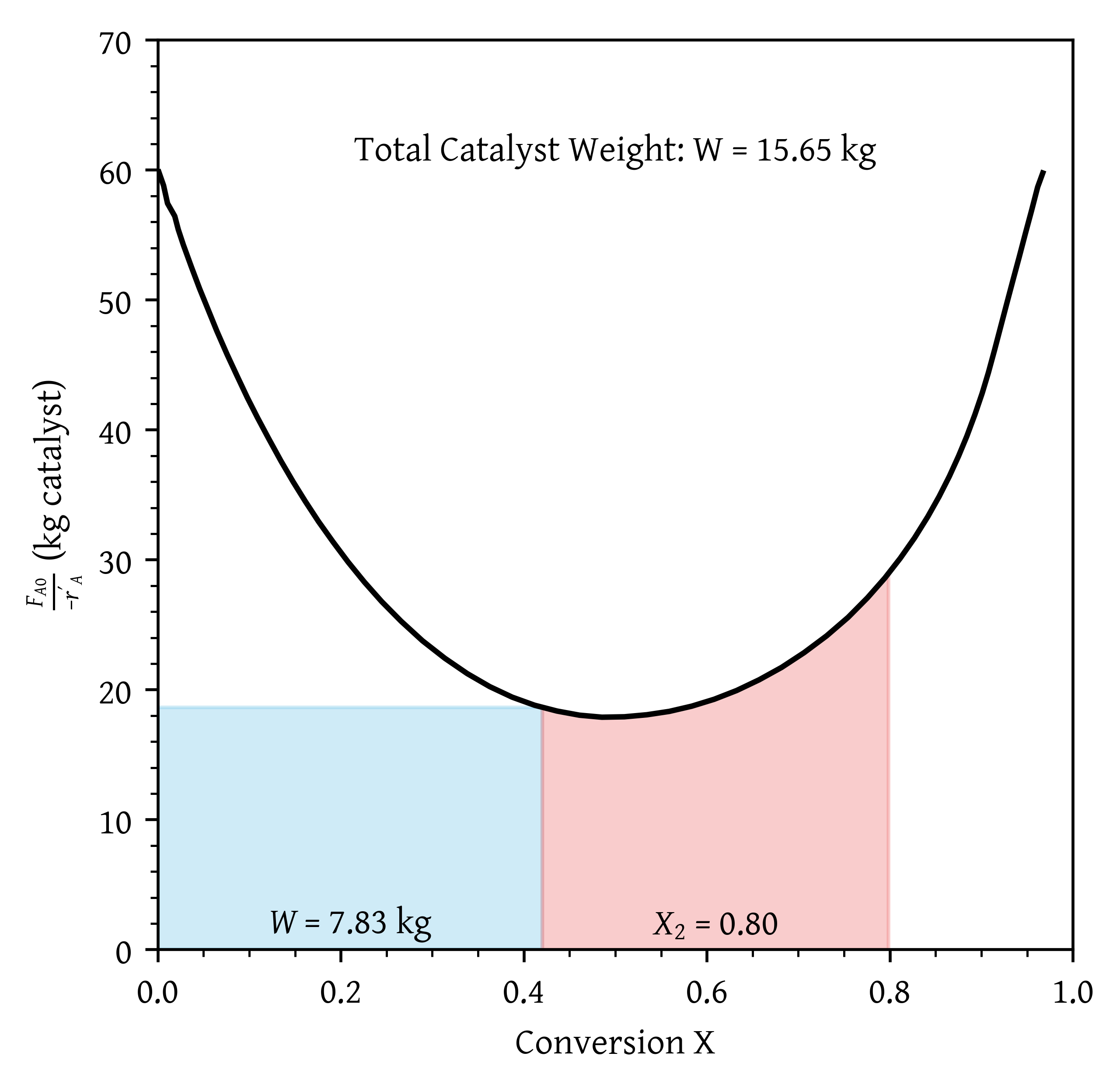
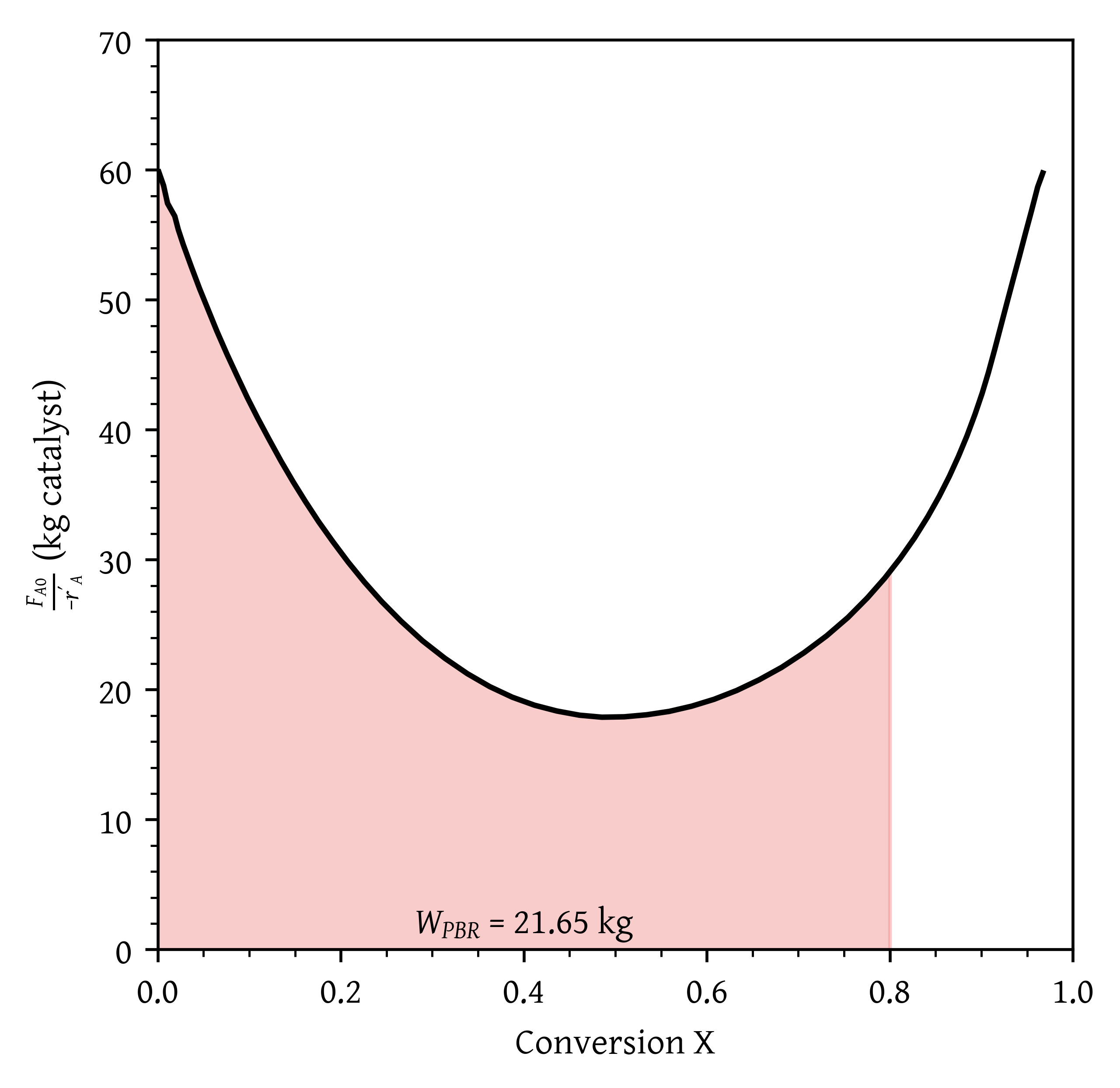
- Assuming that you have a fluidized CSTR and a PBR containing equal weights of catalyst, how should they be arranged for this adiabatic reaction? Use the smallest amount of catalyst weight to achieve 80% conversion of A. (Figure 23)
- What is the catalyst weight necessary to achieve 80% conversion in a fluidized CSTR? (Figure 24)
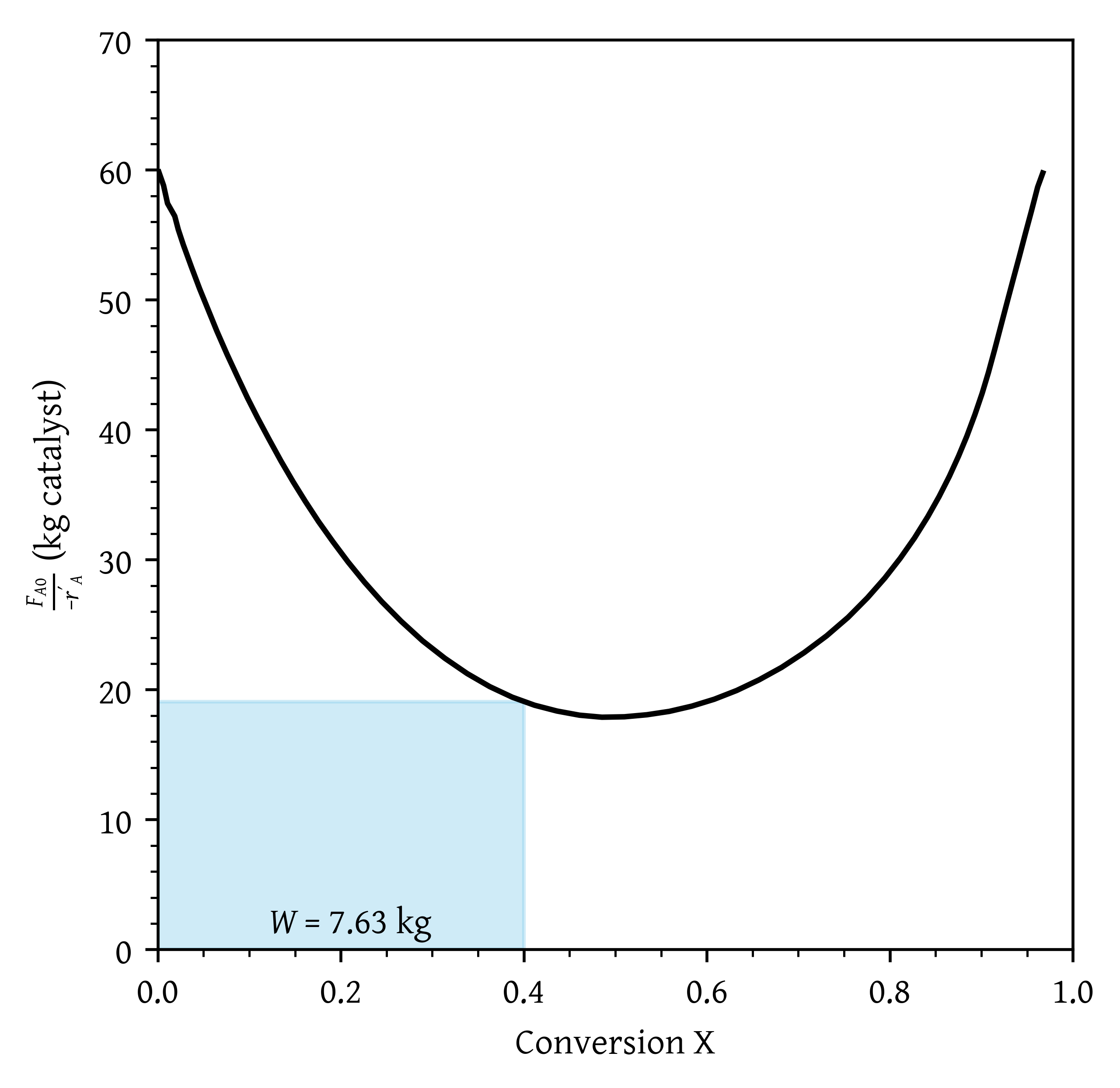
- What fluidized CSTR weight is necessary to achieve 40% conversion? (Figure 25)
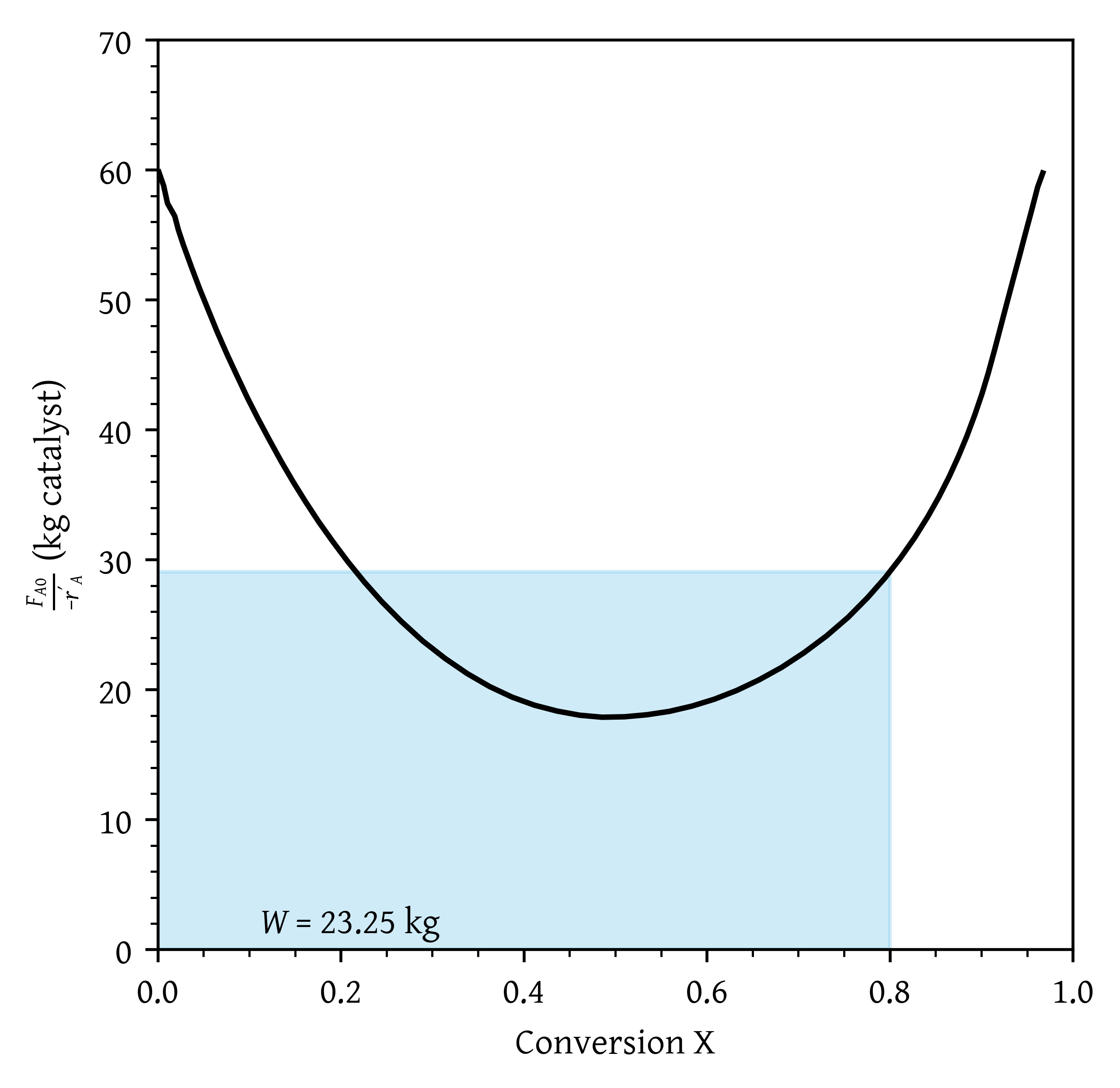
- What PBR weight is necessary to achieve 80% conversion? (Figure 26)
- What PBR weight is necessary to achieve 40% conversion? (Figure 27)
- Plot the rate of reaction and conversion as a function of PBR catalyst weight, W. (Data table: Table 4; Plots: Figure 28)
| 0.0730885 | 0.00122266 | 0.0334255 |
| 1.597 | 0.02795 | 0.0368764 |
| 3.97751 | 0.0756876 | 0.0436557 |
| 6.4248 | 0.134583 | 0.0531844 |
| 8.88462 | 0.207988 | 0.0670574 |
| 11.6107 | 0.313744 | 0.089225 |
| 14.0622 | 0.436315 | 0.108972 |
| 16.2747 | 0.55899 | 0.109126 |
| 18.6969 | 0.681754 | 0.0921045 |
| 21.4901 | 0.794571 | 0.0699448 |
| 23.7561 | 0.865033 | 0.0549146 |
| 25.4624 | 0.907618 | 0.0450597 |
| 27.1073 | 0.941305 | 0.037535 |
Citation
@online{utikar2024,
author = {Utikar, Ranjeet},
title = {Workshop 02 {Solution:} {Conversion} and Reactor Sizing},
date = {2024-03-03},
url = {https://cre.smilelab.dev/content/workshops/02-conversion-and-reactor-sizing/solutions.html},
langid = {en}
}