In class activity: Mole balances

Lecture notes for chemical reaction engineering

Problems

1. Chloral is being consumed at a rate of 10 moles per second per m³ when reacting with chlorobenzene to form DDT and water in the reaction described above. In symbol form, the reaction is written as

   \ce{A + 2B -> C + D}

   Write the rates of disappearance and formation (i.e., generation) for each species in this reaction.

   Solution

   • Rate of disappearance of A: -r_A = 10 mol/m^3 \ s
   • Rate of disappearance of B: -r_B = 2*10 = 20 mol/m^3 \ s
   • Rate of formation of C: r_C = 10 mol/m^3 \ s
   • Rate of formation of D: r_D = 10 mol/m^3 \ s

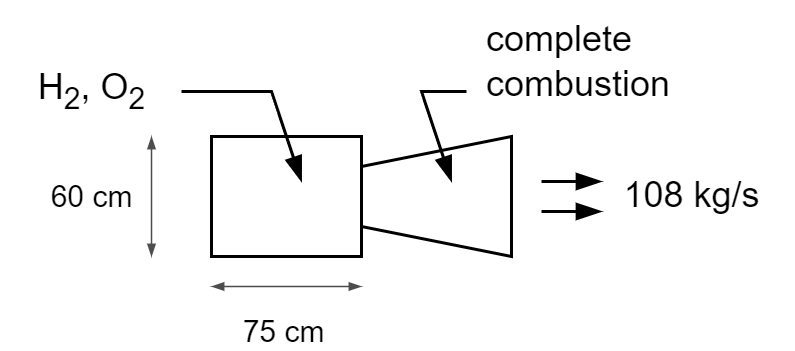
2. A rocket engine, burns a stoichiometric mixture of fuel (liquid hydrogen) in oxidant (liquid oxygen). The combustion chamber is cylindrical, 75 cm long and 60 cm in diameter, and the combustion process produces 108 kg/s of exhaust gases. If combustion is complete, find the rate of reaction of hydrogen and of oxygen.

   

   Figure 1: Rocket engine

   Solution

   V = 0.2121 m^3

   Reactions occuring: \ce{H2 + 1/2 O2 -> H2O}

   Molecular weights: \ce{H2} = 2gm; \ce{O2} = 16gm; \ce{H2O} = 18gm

   • \ce{H2O} produced: 108/18 = 6 kmol/s
   • \ce{H2} used: 6 kmol/s
   • \ce{O2} used: 3 kmol/s

3. A human being (75 kg) consumes about 6000 kJ of food per day. Assume that I the food is all glucose and that the overall reaction is

   \ce{C6H12O6 + 6 O2 -> 6 CO2 + 6 H2O}, -\Delta H_r = 2816 kJ/mol

   Find man’s metabolic rate (the rate of living, loving, and laughing) in terms of moles of oxygen used per m³ of person per second. Assume average density of a human being to be 1000 kg/m^3.

   Solution

   We want to find

   -r'''_{O_2} = -\frac{1}{V_{person}} \frac{dN_{O_2}}{dt} \left[ \frac{mol O_2 used}{m^3 of \ person \ s}\right]

   \rho_{person} = 1000 kg/m^3

   V_{person} = 75/1000 = 0.075 m^3

   Each mole of glucose consumed uses 6 moles of oxygen and releases 2816 kJ of energy

   \frac{dN_{O_2}}{dt} = \left( \frac{6000 \ kJ/day}{2816 \ kJ/mol\ glucose} \frac{6 mol\ O_2}{1 mol\ glucose}\right) = 12.8 \frac{mol O_2}{day}

   -r'''_{O_2} = \frac{1}{0.075} \frac{12.8}{24 \cdot 3600} = 0.002 \frac{mol \ O_2 \ used}{m^3 s}

4. Consider the liquid phase cis – trans isomerization of 2–butene which we will write symbolically as

   cis- \ce{CH3HC=CHCH3} \rightarrow trans- \ce{CH3HC=CHCH3}

   The reaction is first order in A (–r_A = kC_A) and is carried out in a tubular reactor in which the volumetric flow rate,v, is constant, i.e.,v = v_0.

   1. Sketch the concentration profile.
   2. Derive an equation relating the reactor volume to the entering and exiting concentrations of A, the rate constant k, and the volumetric flow rate.
   3. Determine the reactor volume, V_1, necessary to reduce the exiting concentration to 10% of the entering concentration, i.e., C_A = 0.1 C_{A0}, when the volumetric flow rate is 10 dm^3/min (i.e., liters/min) and the specific reaction rate, k, is 0.23 1/min.
   Solution

   Concentration Profile

   

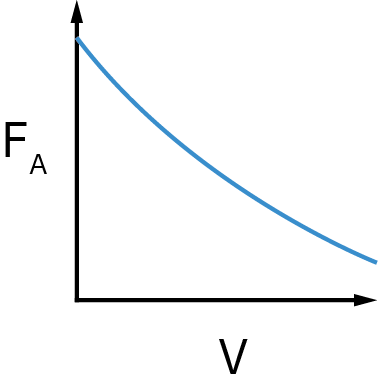
   PFR concentration profile schematic

   Rate equation: –r_A = kC_A

   PFR mole balance: \frac{dFA}{dV} = \frac{dC_A \upsilon_0}{dV} = r_A = - kC_A

   \frac{\upsilon_0}{k} \int_{C_{A_0}}^{C_A} \frac{dC_A}{C_A} = \int_0^V dV

   \frac{\upsilon_0}{k} \ln \frac{C_{A_0}}{C_A} = V

   import math
   
   # Data given
   
   k = 0.23             # 1/min
   Ca0_by_Ca = 1/ 0.1
   upsilon_0 = 10       # dm^3/min 
   
   V = (upsilon_0/k)* math.log(Ca0_by_Ca)

   V = 100.11 m^3