Solutions to workshop 09: External diffusion effects

Lecture notes for chemical reaction engineering

P 14-9

The irreversible gas-phase reaction

\ce{ A ->[ cat ] B}

is carried out adiabatically over a packed bed of solid catalyst particles. The reaction is first order in the concentration of A on the catalyst surface

-r_{As}' = k' C_{As}

The feed consists of 50% (mole) A and 50% inerts, and enters the bed at a temperature of 300 K. The entering volumetric flow rate is 10 dm³/s (i.e., 10,000 cm³/s). The relationship between the Sherwood number and the Reynolds number is

Sh = 100 Re^{1/2}

As a first approximation, one may neglect pressure drop. The entering concentration of A is 1.0 M. Calculate the catalyst weight necessary to achieve 60% conversion of A for

1. isothermal operation.

2. adiabatic operation.

Additional information:

• Kinematic viscosity: \mu/\rho = 0.02 cm^2/s
• Particle diameter: d_p = 0.1 cm
• Superficial velocity: U =10 cm/s
• Catalyst surface area/mass of catalyst bed: a= 60 cm^2/g-cat
• Diffusivity of A: D_e = 10^{-2} cm^2/s
• Heat of reaction: \Delta H_{Rx}^{\circ} = 10,000 cal/g mol A
• Heat capacities: C_{pA} = C_{pB} = 25 cal/g mol \cdot K, C_{pS}\, \text{(solvent)} = 75 cal/g mol \cdot K
• k' (300 K) = 0.01 cm^3 /s \cdot g-cat \; \text{with}\; E = 4000 cal/mol

Solution

Hand written solution

import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import solve_ivp

# constants

RCAL = 1.987  # cal⋅/ mol K

# data
NU_VIS = 0.02 # cm^2/s
DP = 0.1  # cm
VEL = 10 # cm/s
SP_AREA = 60 # cm^2/g-cat
DE = 1e-2 # cm^2/s
DELTA_HR_TR = 10000 # cal/gmol A
CPA = 25 # cal/gmol K
CPB = 25 # cal/gmol K
CPS = 75 # cal/gmol K -- Solvent is inert

KA0 = 0.01 # cm^3/s g-cat
EA0 = 4000 # cal/mol
TR = 300 # K

# Functions
k = lambda t: KA0 * np.exp((EA0 / RCAL) * ((1 / TR) - (1 / t)))

def reactor(w, y, *args):
   # convert dependent variables
   x = y[0]
   (t0, ca0, fa0, phia, phis, kc) = args

   # isothermal case
   t = t0

   # Adiabatic case
   t = t0 + (x * DELTA_HR_TR / (phia * CPA + phis * CPS))

   ca = ca0 * (1-x) * (t0/t)
   rate =  k(t) * kc * ca / (k(t) + kc)

   dxdw = rate / fa0

   dydw = [dxdw]
   return dydw

# Problem data
ca0 = 1.0e-3 # mol/cm^3
v0 = 1.0e4 # cm^3/s
t0 = 300
phia = 1 # 50% A in inlet
phis = 1 # 50% A in inlet

Re = DP * VEL/ NU_VIS 
Sh = 100 * Re**0.5

kc = Sh * DE/DP # cm/s
kc = kc * SP_AREA # cm^3 /s g-cat

fa0 = ca0 * v0

args = (t0, ca0, fa0, phia, phis, kc)

initial_conditions = np.array([0])
w_final = 1e6 # 1000 kg 

sol = solve_ivp(
    reactor,
    [0, w_final],
    initial_conditions,
    args=args,
    method="LSODA",
    dense_output=True,
)

# Extract solution
w = np.linspace(0, w_final, 1000)

# conversion
x = sol.sol(w)[0]

# isothermal case
t = np.full(len(w), t0)

# adiabatic case
t = t0 + (x * DELTA_HR_TR / (phia * CPA + phis * CPS))

k_c = 4242.641 cm^3/s\ g-cat

C_{A0} = 0.001 mol/cm^3

F_{A0} = 10.000 mol/s

T_0 = 300.000 K

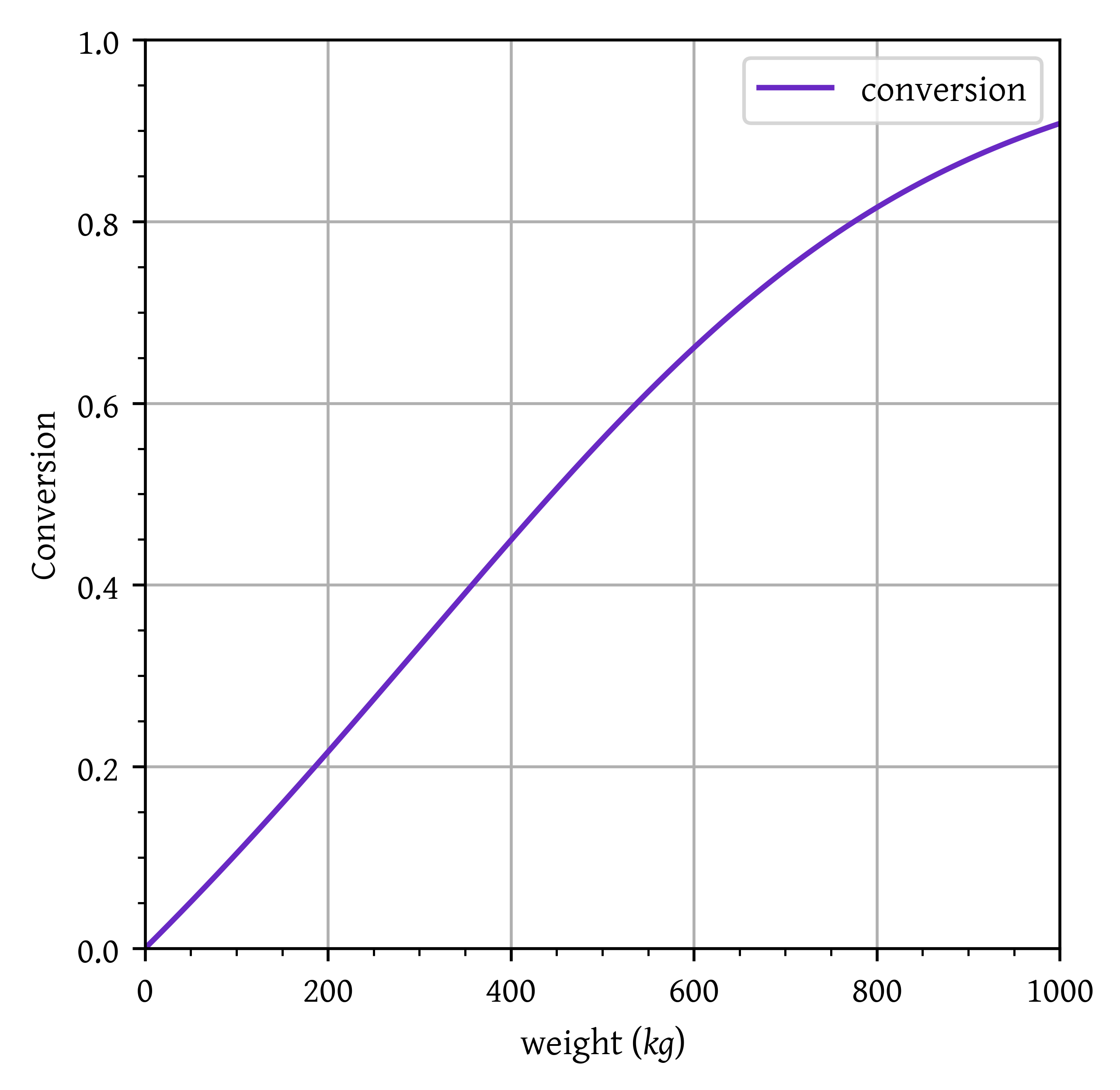
Catalyst weight required for X = 0.6: 538.539 kg

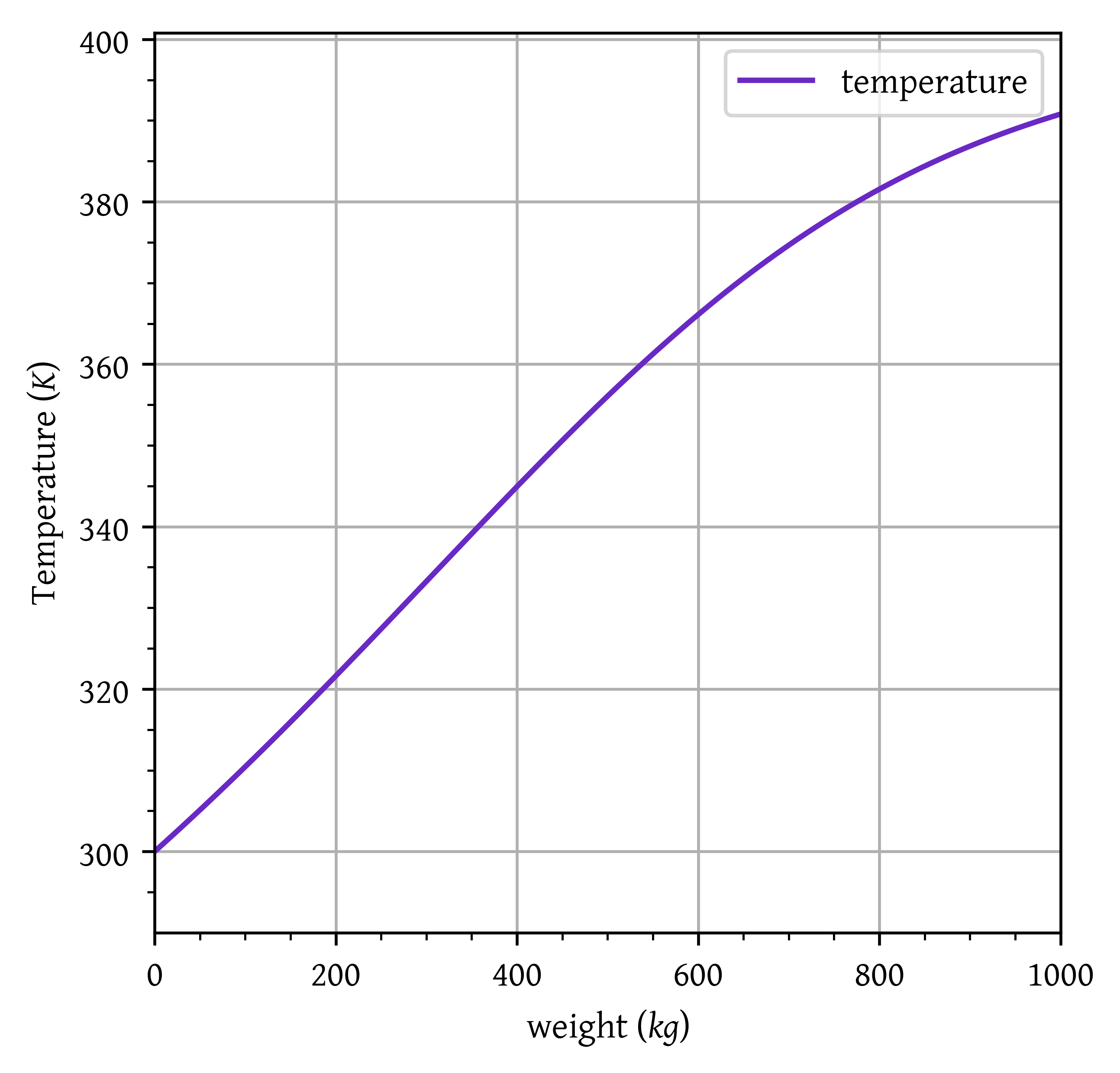
Temperature: 360.08 K

plt.plot(w/1000, x, label="conversion")
plt.xlim(w[0]/1000, w[-1]/1000)
plt.ylim(0, 1)
plt.grid()
plt.legend()

plt.xlabel("weight ($kg$)")
plt.ylabel("Conversion")

plt.show()

Figure 1: Conversion

plt.plot(w/1000, t, label="temperature")
plt.xlim(w[0]/1000, w[-1]/1000)
plt.ylim(t[0]-10, t[-1]+10)
plt.grid()
plt.legend()

plt.xlabel("weight ($kg$)")
plt.ylabel("Temperature ($K$)")

plt.show()

Figure 2: Temperature