Portfolio 06: Nonisothermal reactor design

CHEN3010/ CHEN5040: chemical reaction engineering

Student ID:

General Instructions for in class Portfolios

1. The portfolio is an open-book task.
2. You can use textbooks, the resources provided during class/ workshop etc. to answer the questions.
3. The portfolio task is made available in both pdf format and as a print.
4. You are free to choose a solution technique. It is not required that you use the provided python code to answer the questions. You can use any tool (pen and paper, excel, … ) and any technique (graphical, numerical, analytical) that you are comfortable with.
5. Irrespective of your solution method, you are expected to write your answers on to the printed question paper provided. This is what gets marked.
6. The portfolio will take place during designated time slot communicated earlier by the unit coordinator. Please refer to the portfolio schedule on blackboard for the portfolio dates and topics.
7. The tasks will be a mix of theory questions, short calculation type and long numerical examples.
8. You have 50 minutes to complete the tasks in the portfolio.
9. The portfolios will be marked immediately after completion by your peers using a provided marking rubric.
10. The portfolios will be collected by the instructors to verify peer marking and record the marks. You will receive your portfolio back within a week.
11. When you are required to upload the portfolio answers on to blackboard:
    • Save your report as a pdf file.
    • Rename the file as STUDENTID_Portfolio_x.pdf (Where STUDENTID is your student ID, and x is the portfolio number) and
    • Upload it using assessment submission link on blackboard.

Academic Integrity

Academic integrity at its core is about honesty and responsibility and is fundamental to Curtin’s expectations of you. This means that all of your work at Curtin should be your own and it should be underpinned by integrity, which means to act ethically, honestly and with fairness.

As a Curtin student you are part of an academic community and you are asked to uphold the University’s Code of Conduct, principles of academic integrity, and Curtin’s five core values of integrity, respect, courage, excellence and impact during your studies.

You are also expected to uphold the Student Charter and recognize that cheating, plagiarism collusion, and falsification of data and other forms of academic dishonesty are not acceptable.

For more information, visit https://students.curtin.edu.au/essentials/rights/academic-integrity/

Introduction

The ethylene (E) epoxydation is to be carried out using a cesium-doped silver catalyst in a packed-bed reactor.

\ce{C2H4 + 1/2 O2 -> C2H4O} \qquad \Delta H_{rxn, 1} = -0.17 \ kJ/mol \tag{1}

Along with the desired reaction, the complete combustion of ethylene also occurs

\ce{C2H4 + 3O2 -> 2CO2 + 2H2O} \qquad \Delta H_{rxn, 2} = -1306 \ kJ/mol \tag{2}

Lafarga et al. (2000) have proposed following reaction kinetics for the reaction system.

-r_{1E} = \frac{k_{1E} P_E P_O^{0.58}} {(1 + K_{1E}P_E)^2} \tag{3}

-r_{2E} = \frac{k_{2E} P_E P_O^{0.3}} {(1 + K_{2E}P_E)^2} \tag{4}

The reaction rate constants are:

k_{1E} = 0.15 \ \frac{mol}{kg \cdot s\ atm^{1.58}} \text{ at 523 K with } E_1 = 60.7 \ kJ/mol \tag{5}

k_{2E} = 0.0888 \ \frac{mol}{kg \cdot s\ atm^{1.3}} \text{ at 523 K with } E_2 = 73.2 \ kJ/mol \tag{6}

The adsorption constants are: K_{1E} = 6.50 \ atm^{-1}; \text{ and } K_{2E} = 4.33 \ atm^{-1}

The feed enters the reactor at 250 °C and a pressure of 2 atm. The molar flow rate is 0.0093 mol/s. The reactor contains 100g of catalyst. Pressure drop in the reactor can be neglected. Inlet gas composition along with thermochemical data for the species involved is given in Table 1.

Table 1: Inlet gas composition

Gas	volume fraction at inlet (%)	\Delta H_f^0 at 298 K (kJ/mol)	C_P (J/mol\ K)
\ce{C2H4}	6	-52.47	65
\ce{O2}	12	0	30
\ce{C2H4O}	0	-52.64	80
\ce{CO2}	0	-393.5	45
\ce{H2O}	0	-285.83	35
\ce{N2}	82	0	30

Questions

1. Assuming isothermal conditions, what conversion and selectivity of ethylene oxide to \ce{CO2} are expected at the exit of the PBR? (10 marks)

Answer:

Conversion: X = 1 - \frac{ F_E }{ F_{ E0 } }

Selectivity: Y_{EO/\ce{CO2}} = \frac{ F_{EO} }{ F_{\ce{CO2}} }

Add following code at the end of the supplied file to calculate conversion and selectivity.

x = 1 - f_e/f0[0]
sel = f_eo/f_co2

print (x[-1], sel[-1])

Conversion: 0.674

Selectivity: 0.397 (mol EO/ mol \ce{CO2})

2. The reactor is cooled by boiling kerosene with a boiling point of 250 °C (The ambient temperature can be assumed to be constant at 250 °C). The heat transfer coefficient for the system is Ua = 300 J/kg-cat \ s \ K.

   Write energy balance for the system. (10 marks)

Answer

\frac{dT}{dV} = \frac{ \sum_i^{n_{rxn}} r_i \Delta H_{Rx,i}(T) - Ua (T - T_a) }{ \Sigma_j^{n} F_j C_{P_j} } \tag{7}

\Delta H_{Rx,i}(T) = \Delta H_{Rx,i}^\circ(T_R) + \Delta C_{P,i}(T - T_R) \tag{8}

\sum_i^{n_{rxn}} r_i \Delta H_{Rx,i}(T) = r_{1E} \Delta H_{Rx,2} + r_{2E} \Delta H_{Rx,2} \tag{9}

As the temperature of surrounding is constant, dT_a/dW = 0

3. What would happen if the reactor is operated adiabatically? (10 marks)

   Modify the code given in appendix to include energy balance. Simulate adiabatic operations and report the temperature, conversion, and selectivity for adiabatic operations. Briefly comment on the results.

Answer:

Add following code after the comments

  # non-isothermal case
  # replace dtdw with appropriate expression

  qg = -r0 * delta_hr[0] - r1 * delta_hr[1]
  qr = ua * (t - ta)

  sum_fcp = np.sum(f * CP)

  dtdw =  (qg - qr)/sum_fcp

Set Ua = 0 to simulate adiabatic operations.

As reaction 2 ( Equation 2 ) is highly exothermic, adiabatic operations lead to runaway reaction.

For the given conditions, within a few grams of catalyst, the reactor temperature shoots above 700 °C and the simulation does not run.

Therefore, no data on temperature, conversion, or selectivity could be obtained.

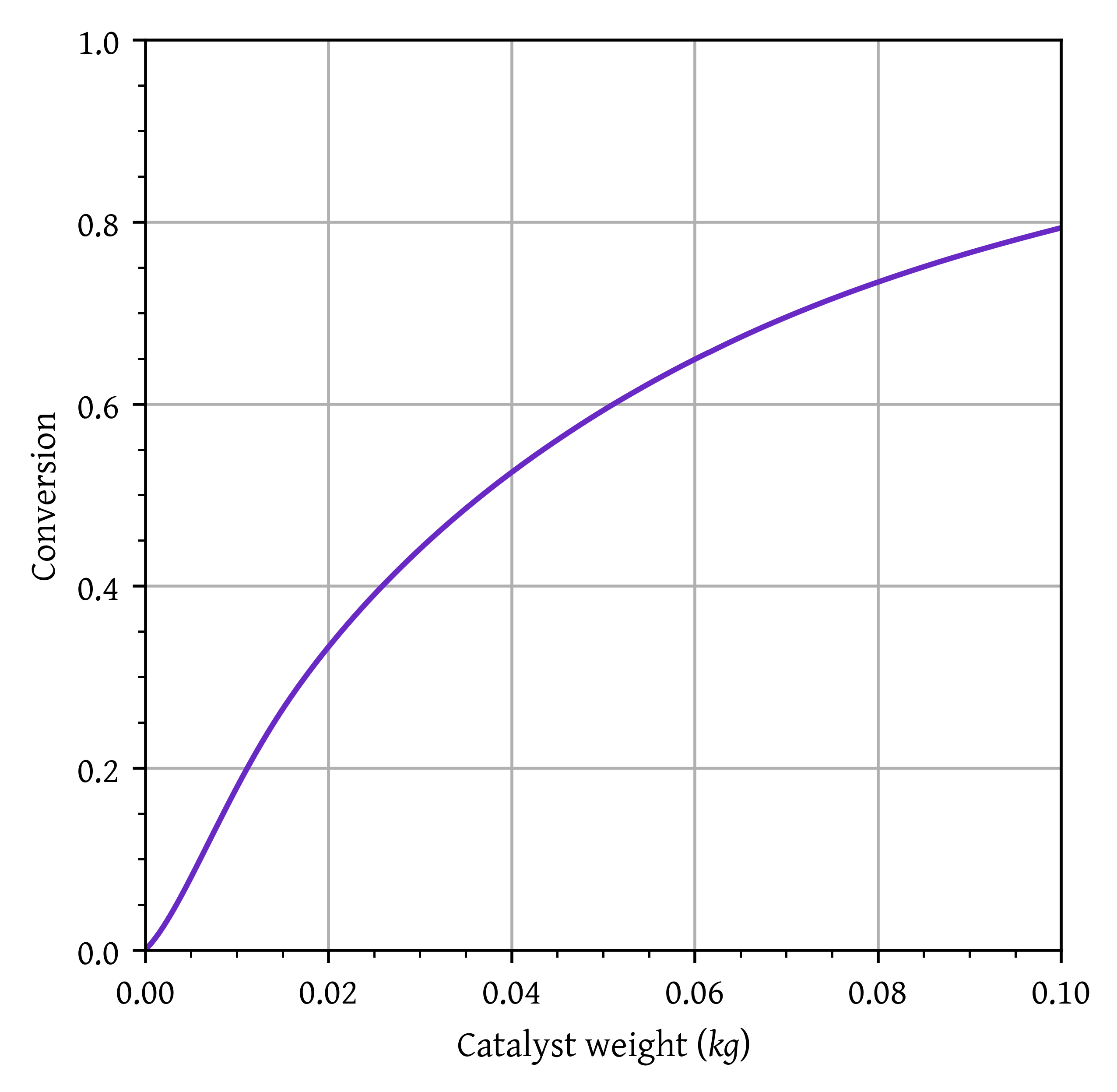
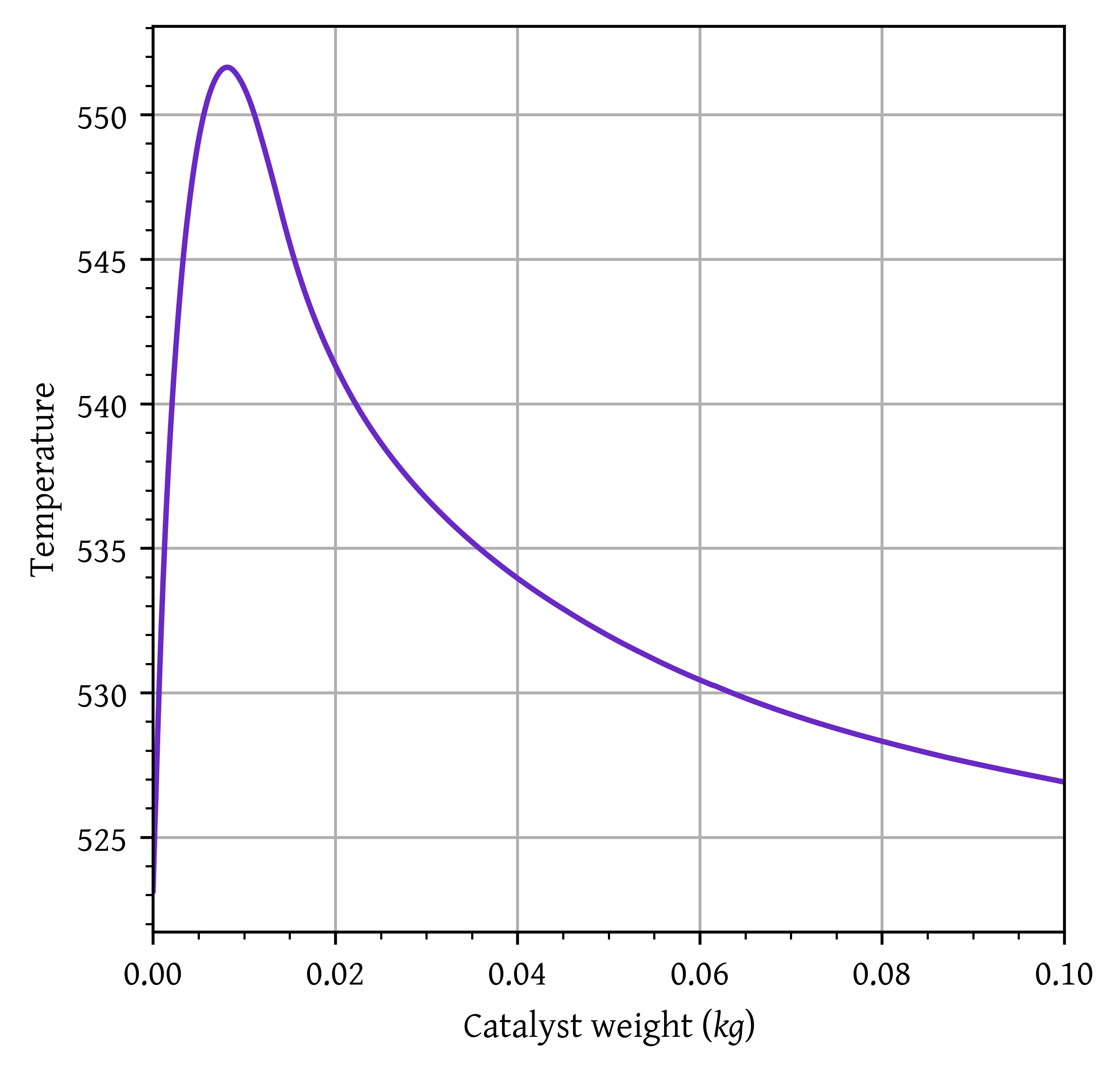
4. Using the conditions for heat transfer fluid in question 2, calculate the maximum temperature in the reactor, the temperature, conversion, and selectivity at the exit of the reactor considering heat transfer. Briefly comment on the results. (10 marks)

Answer:

Set Ua = 300 to simulate the reactor considering heat transfer.

Maximum temperature: 551.63 K

conversion: 0.793

selectivity: 0.357

Initially, the reaction rate is high, therefore, the temperature of the reactor shoots up. Due to increased reactor temperature, the driving force for heat transfer increases increasing the heat removed from the reactor.

As the catalyst weight is increased, conversion increases. This reduces the reaction rate, and heat generated. Consequently, the reactor temperature starts dropping and a final temperature of 526.91 K is obtained at the end of the reactor.

The conversion is higher compared to the isothermal case (due to incease in temperature), however the selectivity is lower (0.357 compared to 0.397).

The simulations show that the reactor is highly sensitive to slight changes in operating conditions indicating the control of the reactor would be extremely difficult.

To increase selectivity, the reactor should be operated at lower temperature.

Appendix

The code is also available as ipython notebook. Download the file portfolio_6.ipynb from blackboard. Open Google colab. From menu, click on File > Upload notebook. Upload the downloaded file and modify as per needed.

Below is complete code for non-isothermal case.

import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

# constants

R = 8.314    # J/ (mol K)
RATM = 0.082    # atm dm^3/ (mol K)
TRR = 523    # K

# Components
# 0: ethylene
# 1: oxygen
# 2: ethylene oxide
# 3: CO2
# 4: water
# 5: nitrogen

# Heats of formation at 298 K in J/mol
HF = np.array([-52470, 0, -52640, -393500, -285830, 0])

# Specific Heat Capacities J/mol K
CP = np.array([65, 30, 80, 45, 35, 30])

# reactions
# 0. C2H4 + 1/2 O2 -> C2H4O
# 1. C2H4 + 3O2 -> 2CO2 + 2H2O

# Stoichiometry
NU = np.array([
    [-1, -0.5, 1, 0, 0, 0],  # Reaction 0: C2H4 + 0.5 O2 -> C2H4O
    [-1, -3, 0, 2, 2, 0]     # Reaction 1: C2H4 + 3 O2 -> 2 CO2 + 2 H2O
])

# Adsorption constants (1/atm)
KE0, KE1 = 6.5, 4.33

# Heat of reaction at reference temperature J/mol
DELTA_HR_TR = np.dot(NU, HF)

# Functions

k0e = lambda t: 0.15 * np.exp((60700/R) * ((1/TRR) - (1/t)))
k1e = lambda t: 0.0888 * np.exp((73200/R) * ((1/TRR) - (1/t)))

# rates
r0e = lambda t, pe, po: k0e(t) * pe * po**0.58 / (1 + KE0*pe)**2 
r1e = lambda t, pe, po: k1e(t) * pe * po**0.3 / (1 + KE1*pe)**2 

def pbr(w,y,*args):

  # convert dependent variables
  f = y[:-1] 
  t = y[-1]

  # convert args
  (pt, ua, ta) = args

  # total molar flow rate
  ft = np.sum(f)

  # mol fr. 
  phi = f/ft

  # partial pressures
  p = pt * phi

  # extract partial pressure for ethylene and oxygen
  pe = p[0]
  po = p[1]

  # calculate reaction rates 
  r0 = r0e(t,pe,po)
  r1 = r1e(t,pe,po)
  
  # Could also be written as an array
  # r = np.array([r1e(t,pe,po), r2e(t,pe,po)])

  # calculate rates of individual species
  r_e = -r0 -r1
  r_o = -0.5 * r0 - 3 * r1
  r_eo = r0
  r_co2 = 2 * r1
  r_h2o = 2 * r1
  r_n2 = 0
  
  # could also be written as 
  # ri = np.dot(NU.T, r)

  # write mole balances
  # dfdw = ri

  df_e = r_e
  df_o = r_o
  df_eo = r_eo
  df_co2 = r_co2
  df_h2o = r_h2o
  df_n2 = r_n2

  # energy balance

  delta_cp = np.dot(NU,CP)
  delta_hr = DELTA_HR_TR + delta_cp * (t - 298)

  # isothermal case
  # dtdw = 0
  
  # non-isothermal case
  # replace dtdw with appropriate expression
  qg = -r0 * delta_hr[0] - r1 * delta_hr[1]
  qr = ua * (t - ta)

  sum_fcp = np.sum(f * CP)

  dtdw =  (qg - qr)/sum_fcp


  # dydw = np.append(dfdw,dtdw)
  dydw = [df_e, df_o, df_eo, df_co2, df_h2o, df_n2, dtdw] 

  return dydw
  

# Problem data

# Heat transfer properties
ua = 300  # J/kg-cat s K

ta = 250 + 273.15 # k

# Inlet pressure and temperature
t0 = 250 + 273.15 # K
p0 = 2 # atm

# inlet flow rate mol/s
ft0 = 0.0093 

# Inlet volume (mol) fraction
phi = np.array([0.06,0.12,0,0,0,0.82])

# Inlet molar flow rates for components mol/s
f0  = phi*ft0

# total catalyst weight kg
wcat = 0.1

# Differential equations
# 0: dF_e/dW
# 1: dF_o/dW
# 2: dF_eo/dW
# 3: dF_co2/dW
# 4: dF_h2o/dW
# 5: dF_n2/dW
# 6: dT/dW

initial_conditions = np.append(f0,t0)
args = (p0, ua, ta)

w_final = wcat

sol = solve_ivp(pbr, 
                [0, w_final], 
                initial_conditions, 
                args=args, 
                method='LSODA',
                dense_output=True)

# Extract solution

w = np.linspace(0,w_final, 1000)

# molar flow rate
f = sol.sol(w)[:-1]

f_e = f[0]
f_o = f[1]
f_eo = f[2]
f_co2 = f[3]
f_h2o = f[4]
f_n2 = f[5]

# temperature
t = sol.sol(w)[-1]

# Calculate conversion, selectivity, max temperature etc. as required # after
# this point

x = 1 - f_e/f0[0]
sel = f_eo/f_co2

print (f'Final conversion: {x[-1]:.2f}; Final selectivity :{sel[-1]:.2f}\n')

plt.plot(w,x, label="Conversion")

plt.xlim(w[0],w[-1])
plt.ylim(0,1)
plt.grid()

plt.xlabel('Catalyst weight ($kg$)')
plt.ylabel('Conversion')

plt.show()

Final conversion: 0.79; Final selectivity :0.36

Figure 1: Conversion

plt.plot(w,t, label="Temperature")

plt.xlim(w[0],w[-1])
plt.grid()

plt.xlabel('Catalyst weight ($kg$)')
plt.ylabel('Temperature')

plt.show()

Figure 2: Temperature

References

Lafarga, David, Mohammed A. Al-Juaied, Christina M. Bondy, and Arvind Varma. 2000. “Ethylene Epoxidation on Ag-Cs/α-Al2O3 Catalyst:  Experimental Results and Strategy for Kinetic Parameter Determination.” Industrial & Engineering Chemistry Research 39 (7): 2148–56. https://doi.org/10.1021/ie990939x.