Portfolio 03: Isothermal reactor design

CHEN3010/ CHEN5040: chemical reaction engineering

General Instructions for take home Portfolios

1. The portolio is an open-book task.
2. It is expected that you will complete the portfolio assessment on your own. You can use textbooks, the resources provided during class/ workshop etc. to answer the questions.
3. You are free to choose a solution technique. It is not required that you use the provided python code to answer the questions. You can use any tool (pen and paper, excel, … ) and any technique (graphical, numerical, analytical) that you are comfortable with. However, some of the tasks will require use of coding/ computer.
4. The tasks will be a mix of theory questions, short calculation type and long numerical examples.
5. The portfolio tasks are not meant to take a lot of time. If you have understood and practiced the relevant content, it should take you around 2 to 3 hours at the most.
6. You are required to upload the portolio answers on to blackboard:
   • Save your report as a pdf file (Miri students should save it as a word file).
   • Rename the file as STUDENTID_Portfolio_x.pdf (Where STUDENTID is your student ID, and x is the portfolio number) and
   • Upload it using assessment submission link on blackboard.

Academic Integrity

Academic integrity at its core is about honesty and responsibility and is fundamental to Curtin’s expectations of you. This means that all of your work at Curtin should be your own and it should be underpinned by integrity, which means to act ethically, honestly and with fairness.

As a Curtin student you are part of an academic community and you are asked to uphold the University’s Code of Conduct, principles of academic integrity, and Curtin’s five core values of integrity, respect, courage, excellence and impact during your studies.

You are also expected to uphold the Student Charter and recognise that cheating, plagiarism collusion, and falsification of data and other forms of academic dishonesty are not acceptable.

For more information, visit https://students.curtin.edu.au/essentials/rights/academic-integrity/

Introduction

Ethylene oxide (EO) (\ce{C2H4O}), also known as oxirane, is a colorless, flammable gas with a sweet, ether-like smell. EO is an important industrial chemical used primarily to make ethylene glycol (a key ingredient in antifreeze and polyester fiber) and other chemicals, such as surfactants, detergents, and solvents.

In 2022, global production of EO was nearly 28 millions of tons and s expected to grow at a steady CAGR of 4.07% during the forecast period until 2032. With a selling price of $1913 per tonne, the commercial value of EO is around $53 billion.

The primary route for EO production involves the direct vapor phase oxidation of ethylene in the presence of a silver catalyst:

\ce{C2H4 + 1/2 O2 -> C2H4O}

This reaction is highly exothermic and requires careful control to manage the risk of runaway reactions. The process typically involves a recovery stage to separate EO from water and other byproducts.

We want to design a reactor achieve a desired conversion of ethylene. Ethylene and oxygen (as air) are fed in stoichiometric proportions to a packed-bed reactor operated isothermally at 280 ^\circ C.

Ethylene and oxygen are fed in stoichiometric proportions to a packed-bed reactor operated isothermally at 280 ^\circ C. Ethylene is fed at a rate of 200 mol/s at a pressure of 10 atm (1013 kPa). It is proposed to use 10 banks of 25.4 mm diameter schedule 40 tubes packed with catalyst with 100 tubes per bank. Consequently, the molar flow rate to each tube is to be 0.2 mol/s.

The rate law for the reaction is

-r'_A = k P_A^{1/3} P_B^{2/3}

with k = 0.00392 \frac{mol}{atm \ kg-cat\ s} at 260 ^\circ C. The heat of reaction, \Delta H is -106.7 kJ/mol and the activation energy, E is 69.49 kJ/mol.

Questions

1. Isobaric reactor (10 marks)

   Using the mole balances developed in portfolio 02, determine the weight of catalyst required to achieve 60% conversion in a PBR. Show your working by following the reaction engineering algorithm. State your assumptions if any.

Answer

• Mole balance (1 mark)

  F_{A0}\frac{dX}{dW} = -r'_A \tag{1}

• Rate law (1 mark)

  -r'_A = k P_A^{1/3} P_B^{2/3} \tag{2}

  Where, P_i = C_i RT_0

  k(T) = k(T_0) e^{\frac{E}{R} \left( \frac{1}{T_0} - \frac{1}{T} \right)}

• Stoichiometry (1 mark)

  For isothermal, isobaric reactors C_j = \frac{C_{A0} (\Theta_j + \nu_j X)} {(1 + \epsilon X)} \tag{3}

  Reaction: \begin{aligned} \ce{C2H4 + 1/2 O2} & \ce{-> C2H4O} \\ \ce{A + 1/2 B } & \ce{-> C} \end{aligned}

• Combine (1 mark)

  Solve equations 1, 2, and 3 to obtain conversion as a function of catalyst weight.

• Evaluate (6 mark)

import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

T = 280 + 273.15  # K
T0 = 260 + 273.15 # K
P0 = 10 # atm

k0 = 0.00392 #  mol/ (atm kg-cat s)

R = 0.082    # atm dm^3/ (mol K)
E = 69490    # J/mol

# It is usually a good idea to write k as a function of temperature. However,
# since we are simulating isothermal case, we just evaluate it. 
k = k0 * np.exp((E/8.314) * ((1/T0) - (1/T)))

fa0 = 0.2
fb0 = 0.5 * fa0
fc0 = 0 
fi0 = fb0 * (79/21)

ft0 = fa0 + fb0 + fc0 + fi0

thetaA = fa0/fa0
thetaB = fb0/fa0
thetaC = fc0/fa0
thetaI = fi0/fa0

ya0 = fa0/ft0
delta = -0.5
epsilon = ya0 * delta

pa0 = ya0 * P0
ca0 = pa0/(R * T)

• k at 280 ^\circ C

  k = 0.00392 \frac{mol}{atm \ kg-cat\ s} at 260 ^\circ C.

  k(T) = k(T_0) e^{\frac{E}{R} \left( \frac{1}{T_0} - \frac{1}{T} \right)}

  k at 280 ^\circ C = 0.00691 \frac{mol}{atm \ kg-cat\ s}

\nu_A = -1; \nu_B = -1/2; \nu_C = 1

Ethylene and oxygen are fed in stoichiometric proportions to a packed-bed. The oxygen is fed as air (21% O₂ and 79% N₂ (Inert)).

F_{A0} = 0.20 mol/s

F_{B0} = 0.5 F_{A0} = 0.10 mol/s

F_{C0} = 0.00 mol/s

F_{I0} = 0.5 \times (79/21) = 0.38 mol/s

F_{T0} = 0.68 mol/s

\Theta_i = F_{i0}/F_{A0}: \Theta_A = 1.00 , \Theta_B = 0.50 , \Theta_C = 0.00 , \Theta_I = 1.88 mol/s.

\delta = 1 - 1 - \frac{1}{2} = -\frac{1}{2}

y_{A0} = F_{A0}/ (F_{A0} + F_{B0}) = 0.30.

\epsilon = y_{A0} \delta = -0.15.

P_{A0} = y_{A0} P_0 = 2.96 atm

C_{A0} = P_{A0} RT = 0.07 mol/dm^3.

def pbr(W, y, *args):
  X = y[0]

  fa0, ca0, thetaA, thetaB, nu_A, nu_B, epsilon, k = args

  ca = ca0 * (thetaA + nu_A * X)/ ( 1 + epsilon * X) 
  cb = ca0 * (thetaB + nu_B * X)/ ( 1 + epsilon * X) 

  pa = ca *(R * T) 
  pb = cb *(R * T)  

  rate = k * pa**(1/3) * pb**(2/3)

  dXdW = rate/ fa0

  return [dXdW]

nu_A = -1
nu_B = -0.5

# Solve the pbr model
W = 25 # kg

# initial conditions
y0 = [0]

system_args = (fa0, ca0, thetaA, thetaB, nu_A, nu_B, epsilon, k)

sol = solve_ivp(pbr, [0, W], y0, args=system_args, dense_output=True)

w = np.linspace(0,W, 1000)
X = sol.sol(w)[0]

x_final = X[X > 0.6][0]
w_final = w[X > 0.6][0]

Weight of catalyst required to achieve a conversion of 60%, W = 13.51 kg. The final conversion is X = 0.60.

• half marks for essentially correct procedure but wrong answers.

2. Effect of pressure drop (20 marks)

   As this is a gas phase reaction carried out in a PBR, there is a significant pressure drop. The properties of the reacting fluid are to be considered identical to those of air at this temperature and pressure. The density of the 6.35 mm catalyst particles is 1925 kg/m^3, the bed void fraction is 0.45, and the gas density is 16 kg/m^3. For these catalyst properties, the pressure drop parameter \alpha is 0.0367 1/kg

   1. How will the equations change when you consider pressure drop?

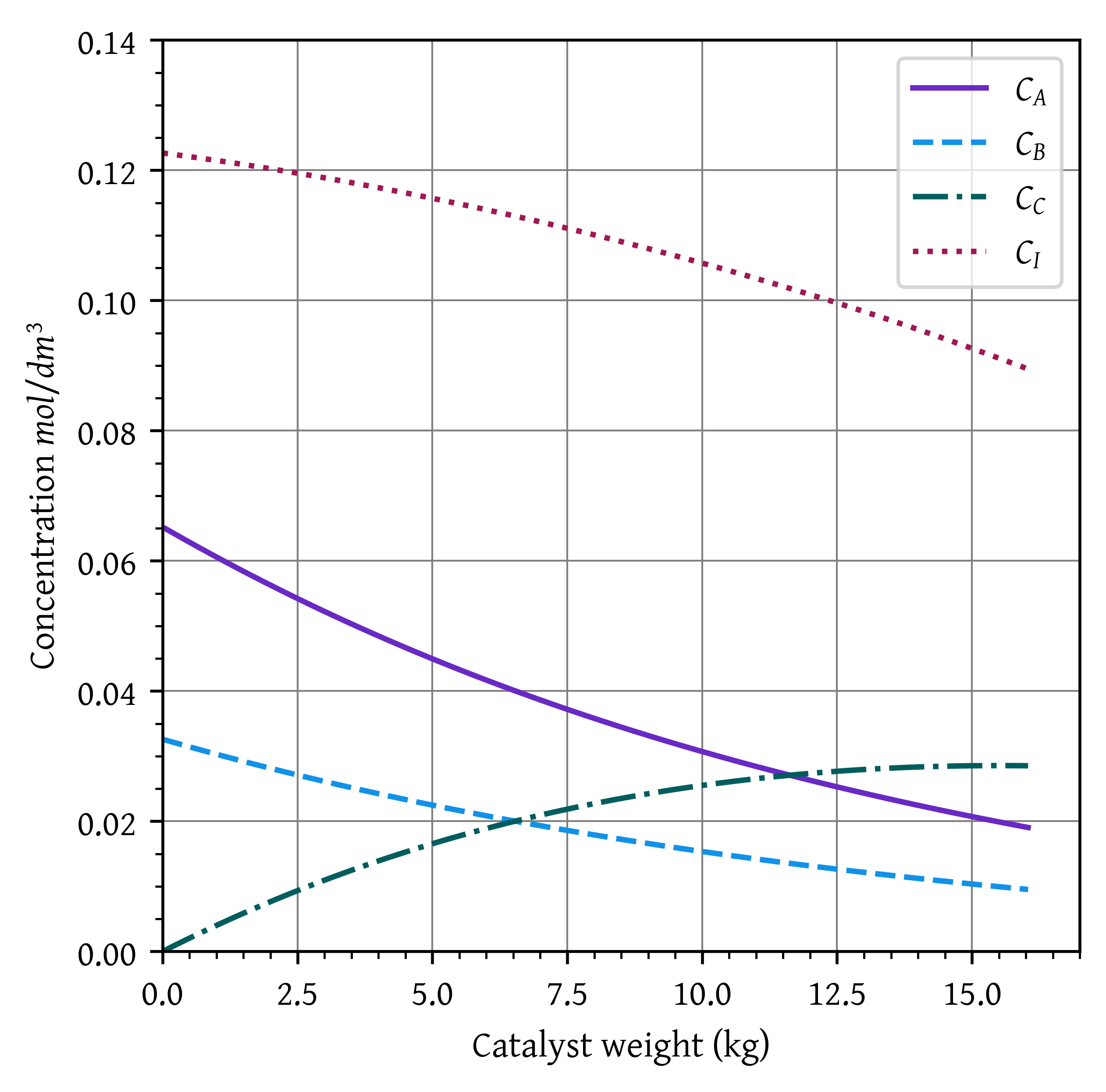
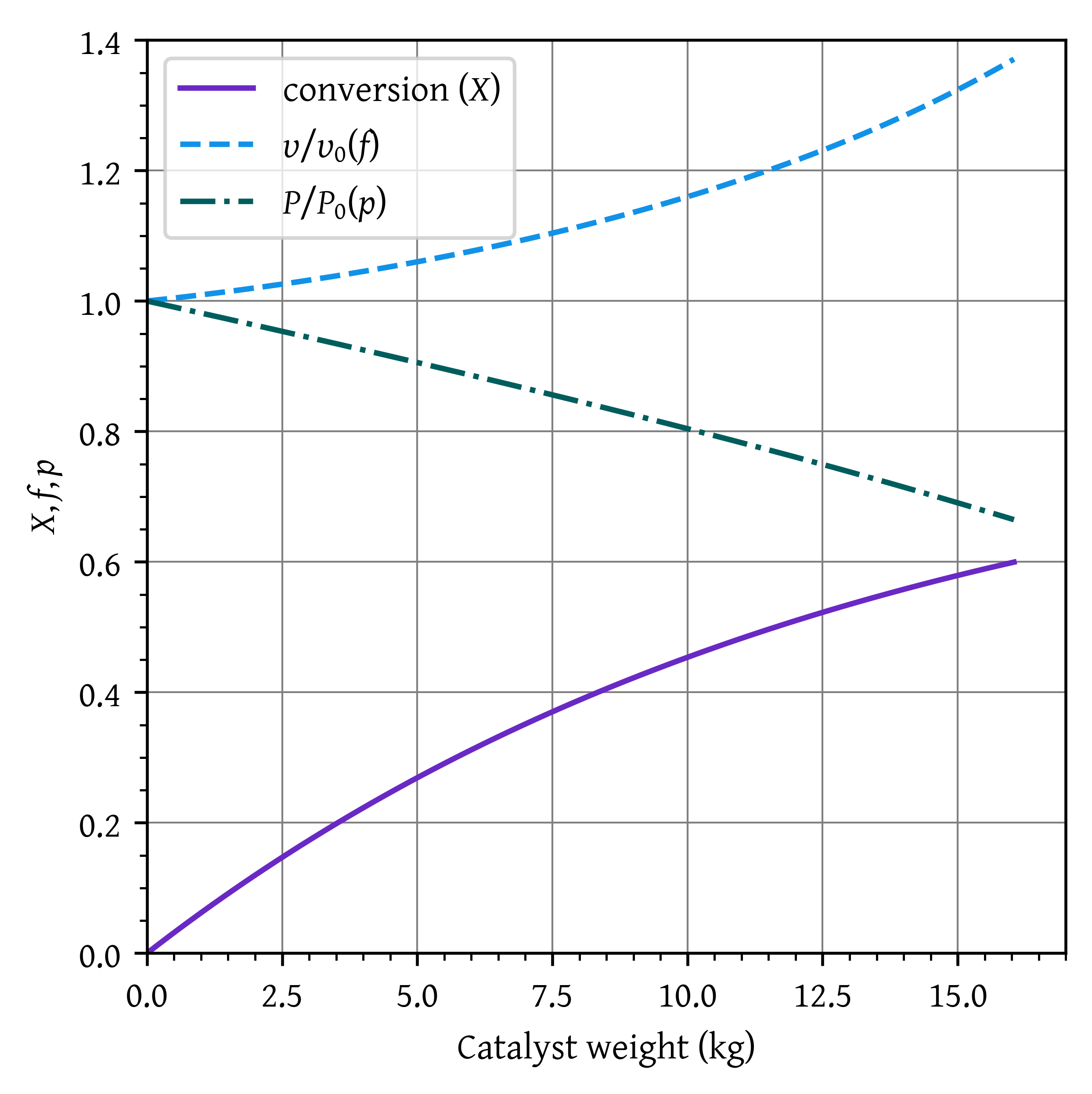
   2. Draw the profiles of concentrations of reactants and products, conversion, volumetric flow rate ratio (\upsilon/\upsilon_0), and pressure ratio (P/P_0) as a function of catalyst weight.

   3. Estimate the catalyst weight required to achieve 60% conversion considering pressure drop. Compare the results with those obtained in question 1.

Answer

a. How will the equations change when you consider pressure drop?

• Mole balance (1 mark)

  No change

  F_{A0}\frac{dX}{dW} = -r'_A \tag{4}

• Rate law (1 mark)

  No change

  -r'_A = k P_A^{1/3} P_B^{2/3} \tag{5}

  Where, P_i = C_i RT_0

  k(T) = k(T_0) e^{\frac{E}{R} \left( \frac{1}{T_0} - \frac{1}{T} \right)}

• Stoichiometry (1 mark)

  The reator is no more isobaric

  For isothermal reactors

  \frac{\upsilon}{\upsilon_0} = (1 + \epsilon X) \left( \frac{P_0}{P}\right)

  C_j = \frac{C_{A0} (\Theta_j + \nu_j X)} {(1 + \epsilon X)} \left( \frac{P}{P_0} \right) \tag{6}

  Reaction: \begin{aligned} \ce{C2H4 + 1/2 O2} & \ce{-> C2H4O} \\ \ce{A + 1/2 B } & \ce{-> C} \end{aligned}

• Pressure drop (1 mark)

  \frac{dp}{dW} = -\frac{\alpha}{2p} \left( 1 + \epsilon X \right) \tag{7}

  Where: p = P/P_0

• Combine

  Solve equations 4, 5, 6, and 7 to obtain conversion as a function of catalyst weight.

• Evaluate (6 marks)

def pbr_with_pressure_drop(W, y, *args):
  
  X,p = y
  fa0, ca0, thetaA, thetaB, nu_A, nu_B, epsilon, k, alpha = args
  
  ca = ca0 * (thetaA + nu_A * X)/ ( 1 + epsilon * X) * p 
  cb = ca0 * (thetaB + nu_B * X)/ ( 1 + epsilon * X) * p

  pa = ca * R * T 
  pb = cb * R * T  

  rate = k * pa**(1/3) * pb**(2/3)
  
  dXdW = rate/ fa0
  
  dpdW = - alpha * (1 + epsilon * X) / (2 * p)

  return [dXdW, dpdW]

nu_A = -1
nu_B = -0.5
nu_C = 1
nu_I = 0

# Solve the pbr model
W = 25 # kg

# initial conditions
# at W = 0 , X = 0; p = 1
y0 = [0, 1]

alpha = 0.0367
system_args = (fa0, ca0, thetaA, thetaB, nu_A, nu_B, epsilon, k, alpha)

sol = solve_ivp(
    pbr_with_pressure_drop, 
    [0, W], 
    y0, 
    args=system_args, 
    dense_output=True
)

w = np.linspace(0,W, 1000)
X = sol.sol(w)[0]
p = sol.sol(w)[1]

x_final_2 = X[X > 0.6][0]
w_final_2 = w[X > 0.6][0]

b. Draw the profiles

# Concentrations
# C_j = C_A0 * (Theta_j + nu_j * X) * p/ (1 + epsilon *X)
ca = lambda X, p: ca0 * (thetaA + nu_A * X) * p / (1 + epsilon * X)
cb = lambda X, p: ca0 * (thetaB + nu_B * X) * p / (1 + epsilon * X)
cc = lambda X, p: ca0 * (thetaC + nu_C * X) * p / (1 + epsilon * X)
ci = lambda X, p: ca0 * (thetaI + nu_I * X) * p / (1 + epsilon * X)

# volumetric flow rate ratio
# v/v0 = (1 + epsilon * X) * P_0/P = (1 + epsilon * X)/p
vv0 = lambda X, p: (1 + epsilon * X)/p

# Set up graph

x_p = X[X < 0.6]
p_p = p[X < 0.6]
w_p = w[X < 0.6]

ca_p = ca(x_p, p_p)
cb_p = cb(x_p, p_p)
cc_p = cc(x_p, p_p)
ci_p = ci(x_p, p_p)

vv0_p = vv0(x_p, p_p)

plt.plot(w_p, ca_p, label='$C_A$')
plt.plot(w_p, cb_p, label='$C_B$')
plt.plot(w_p, cc_p, label='$C_C$')
plt.plot(w_p, ci_p, label='$C_I$')

plt.xlabel('Catalyst weight (kg)')
plt.ylabel('Concentration $mol/dm^3$')

# Setting x and y axis limits
plt.xlim(0, np.ceil(w_final_2))
plt.ylim(0, 0.14)

plt.legend(loc='upper right')

ax = plt.gca()
ax.grid(which='major', linestyle='-', linewidth='0.5', color='gray')

plt.show()

Figure 1: Concentration profile (2 marks)

plt.plot(w_p, x_p, label='conversion ($X$)')
plt.plot(w_p, vv0_p, label='$\\upsilon/\\upsilon_0 (f)$')
plt.plot(w_p, p_p, label='$P/P_0 (p)$')

plt.xlabel('Catalyst weight (kg)')
plt.ylabel('$X, f, p$')

# Setting x and y axis limits
plt.xlim(0, np.ceil(w_final_2))
plt.ylim(0, 1.4)

plt.legend()

ax = plt.gca()
ax.grid(which='major', linestyle='-', linewidth='0.5', color='gray')
plt.show()

Figure 2: Conversion, volumetric flow ratio, pressure ratio profile (4 marks)

• half marks for essentially correct procedure but wrong answers.

c. Estimate the catalyst weight required to achieve 60% conversion

Weight of catalyst required to achieve a conversion of 60%, W = 16.07 kg. The final conversion is X = 0.60. (2 marks)

As the presesure decreases within the reactor, the cocentration (and consequently the rate) decreases. This results into lower conversion for the same catalyst weight.

For the isobaric case, to achieve a conversion of 0.60, we needed 13.51 kg catalyst. If we used this catalyst weight to manufacture our reactor, the real life conversion would have been 0.55 and our reactor would severely underperform. (2 marks)

• half marks for essentially correct procedure but wrong answers.