In class activity: Reaction mechanisms and catalysis

Lecture notes for chemical reaction engineering

Author

Ranjeet Utikar

Published

March 23, 2024

Modified

May 12, 2024

Gas phase decomposition of azomethane

Consider the gas-phase decomposition of azomethane, AZO, to give ethane and nitrogen

$\ce{(CH3)2N2 -> C2H6 + N2}$

Experimental observations show that the rate of formation of ethane is first order with respect to AZO at pressures greater than 1 atm (relatively high concentrations)

$r_{\ce{C2H6}} \propto C_{AZO}$

and second order at pressures below 50 mmHg (low concentrations):

$r_{\ce{C2H6}} \propto C_{AZO}^2$

We could combine these two observations to postulate a rate law of the form

$r_{\ce{C2H6}} =\frac{ k_1 C_{AZO}^2 } { 1 + k_2 C_{AZO} }$

find a mechanism that is consistent with the experimental observations

Solution

Step 1: Propose an active intermediate.

We will choose as an active intermediate an azomethane molecule that has been excited through molecular collisions, to form $\ce{AZO*}$ , that is, $\ce{[(CH3)2N2]*}$ .

Step 2: Propose a mechanism

Reaction 1: $\ce{(CH3)2N2 + (CH3)2N2 ->[k_{1}] (CH3)2N2 + [(CH3)2N2]* }$

Reaction 2: $\ce{[(CH3)2N2]* + (CH3)2N2 ->[k_{2}] (CH3)2N2 + (CH3)2N2 }$

Reaction 3: $\ce{[(CH3)2N2]* ->[k_{3}] C2H6 + N2}$

Step 3: Write rate laws

Reaction 1: $r_{1} = k_1 C_{AZO}^2$

Reaction 2: $r_2 = -k_2 C_{\ce{AZO*}} C_{\ce{AZO}}$

Reaction 3: $r_3 = -k_3 C_{\ce{AZO*}}$

Step 4: Write rate of formation of product.

$r_{\ce{C2H6}} = k_3 C_{\ce{AZO*}}$

Step 5: Write net rate of formation of the active intermediate and use the PSSH

$r_{\ce{AZO*}} = r_{1} + r_{2} + r_{3}$

$r_{\ce{AZO*}} = k_1 C_{\ce{AZO}}^2 - k_2 C_{\ce{AZO*}} C_{\ce{AZO}} - k_3 C_{\ce{AZO*}} = 0$

Solving for $C_{\ce{AZO*}}$

$C_{\ce{AZO*}} = \frac{k_1 C_{\ce{AZO}}^2} {k_2 C_{\ce{AZO}} + k_3}$

Step 6: Eliminate the concentration of the active intermediate species in the rate laws by solving the simultaneous equations developed in Steps 4 and 5.

$r_{\ce{C2H6}} = \frac{k_1 k_3 C_{\ce{AZO}}^2} {k_2 C_{\ce{AZO}} + k_3}$

Step 7: Compare with experimental data.

At low AZO concentrations, $k_2 C_{\ce{AZO}} \ll k_3$

for which case we obtain the following second-order rate law:

$r_{\ce{C2H6}} = k_1 C_{\ce{AZO}}^2$

At high concentrations $k_2 C_{\ce{AZO}} \gg k_3$

in which case the rate expression follows first-order kinetics

$r_{\ce{C2H6}} = k C_{\ce{AZO}}$

Nitric oxide combustion

Find the reaction rate law of the following reaction

$\ce{2 NO + O2 -> 2 NO2}$

Experimental result: At low $\ce{NO}$ concentration, the reaction rate decreases with increasing temperature.

Solution

Step 1: Propose an active intermediate.

We will choose as an active intermediate $\ce{NO3*}$ .

Step 2: Propose a mechanism

Reaction 1: $\ce{NO + O2 ->[k_{1}] NO3*}$

Reaction 2: $\ce{NO3* ->[k_{2}] NO + O2}$

Reaction 3: $\ce{NO3* + NO ->[k_{3}] 2NO2}$

Step 3: Write rate laws

Reaction 1: $r_{1, \ce{NO3*}} = k_1 C_{\ce{NO}} C_{\ce{O2}}$

Reaction 2: $r_{2, \ce{NO3*}}= -k_2 C_{\ce{NO3*}}$

Reaction 3: $r_{3, \ce{NO2}} = k_3 C_{\ce{NO3*}} C_{\ce{NO}}$

Step 4: Write rate of formation of product.

$r_{\ce{NO2}} = k_3 C_{\ce{NO3*}} C_{\ce{NO}}$

Step 5: Write net rate of formation of the active intermediate and use the PSSH

$r_{\ce{NO3*}} = r_{1} - r_{2} - r_{3}/2$

$r_{\ce{NO3*}} = k_1 C_{\ce{NO}} C_{\ce{O2}} - k_2 C_{\ce{NO3*}} - \frac{k_3}{2} C_{\ce{NO3*}} C_{\ce{NO}} = 0$

Solving for $C_{\ce{NO3*}}$

$C_{\ce{NO3*}} = \frac{k_1 C_{\ce{NO}} C_{\ce{O2}}} {k_2 + \frac{k_3}{2} C_{\ce{NO}}}$

Step 6: Eliminate the concentration of the active intermediate species in the rate laws by solving the simultaneous equations developed in Steps 4 and 5.

At low NO concentrations, $k_2 \gg \frac{k_3}{2} C_{\ce{NO}}$

$C_{\ce{NO3*}} = \frac{k_1}{k_2} C_{\ce{NO}} C_{\ce{O2}}$

$r_{\ce{NO2}} = \frac{k_1 k_3}{k_2} C_{\ce{NO}}^2 C_{\ce{O2}}$

Step 7: Compare with experimental data.

Experimental result: At low $\ce{NO}$ concentration, the reaction rate decreases with increasing temperature.

$r_{\ce{NO2}} = \frac{A_1 A_3}{A_2} \exp\left[ \frac{E_2 - (E_1 + E_3)}{RT}\right] C_{\ce{NO}}^2 C_{\ce{O2}}$

For reaction rate to decrease with temperature, $E_2 > E_1 + E_3$

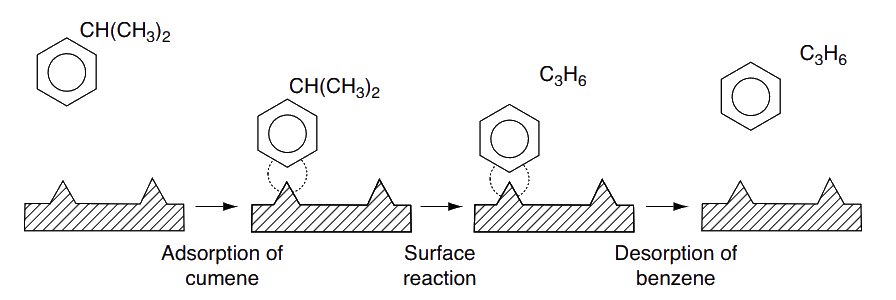
Decomposition of cumene to form benzene and propylene

Develop rate laws for catalytic decomposition of cumene to form benzene and propylene.

$\ce{ C6H5CH(CH3)2 -> C6H6 + C3H6 }$

Solution

Reaction: $\ce{Cumene (C) -> Benzene (B) + Propylene (P)}$

Steps:

Adsorption:

$\ce{ C + S <=>[k_A][k_{-A}] C*S}$

Surface reaction:

$\ce{C*S <=>[k_S][k_{-S}] B*S + P}$

Desorption:

$\ce{B*S <=>[k_D][k_{-D}] B + S}$

Reaction rates:

Adsorption:

$r_{AD} = k_A P_C C_V - k_{-A} C_{\ce{C*S}}; \qquad r_{AD} = k_A \left(P_C C_V - \frac{C_{\ce{C*S}}}{K_A} \right)$

Surface reaction:

$r_{S} = k_S C_{\ce{C*S}} - k_{-S} P_P C_{\ce{B*S}} -; \qquad r_{S} = k_S \left(C_{\ce{C*S}} - \frac{P_P C_{\ce{B*S}}}{K_S} \right)$

Desorption:

$r_{D} = k_D C_{\ce{B*S}} - k_{-D} P_B C_V; \qquad r_{D} = k_D \left(C_{\ce{B*S}} - \frac{P_B C_V}{K_{DB}} \right);$

$K_B = \frac{1}{K_{DB}}; \Rightarrow r_{D} = k_D \left( C_{\ce{B*S}} - K_B P_B C_V \right)$

For steady state operations the reaction rates of these three steps are equal.

$-r'_C = r_{AD} = r_S = r_D$

Case 1: Adsorption of Cumene Rate-Limiting

$-r'_C = r_{AD} = k_A \left(P_C C_V - \frac{C_{\ce{C*S}}}{K_A} \right)$

Because we cannot measure either $C_V$ or $C_{\ce{C*S}}$ , we must replace these variables in the rate law with measurable quantities in order for the equation to be meaningful.

For adsorption-limited reactions, the surface-specific reaction rate $k_S$ , and desorption-specific reaction rate $k_D$ are large by comparison, and we can set

$\frac{r_S}{k_S} \approx 0; \text{ and } \frac{r_D}{k_D} \approx 0$

Therefore,

$C_{\ce{C*S}} = \frac{C_{\ce{B*S}} P_P}{K_S}$

And,

$C_{\ce{B*S}} = K_B P_B C_V$

Combining,

$C_{\ce{C*S}} = K_B \frac{P_B P_P}{K_S} C_V$

and

$-r'_{C} = k_A \left( P_C C_V - \frac{K_B P_B P_P C_V}{K_S K_C} \right)$

The concentration of vacant sites, $C_V$ , can now be eliminated by utilizing the site balance to give the total concentration of sites, $C_t$ which is assumed constant.

$C_t = C_V + C_{\ce{C*S}} + C_{\ce{B*S}}$

$C_t = C_V + \frac{K_B P_B P_P C_V}{K_S} + K_B P_B C_V$

Solving for $C_V$ we have

$C_V = \frac{C_t}{1 + \frac{K_B P_P P_B}{K_S} + K_B P_B}$

and the rate equation

$r'_{C} = \frac{C_t k_A \left( P_C - \frac{P_B P_P}{K_P} \right)} {1 + \frac{K_B P_P P_B}{K_S} + K_P P_B}$

At t = 0 min we have $P_C = P_{C,0}$ , $P_P = 0$ (no product) and $P_B = 0$ (no product)

$-r'_{CO} = r_{AD} = C_t k_A P_{CO} = k P_{CO}$

Plot initial rate $-r'_{C,0} \text{ vs. } P_{C,0}$ is linear.

Case 2: Surface Reaction Rate-Limiting

$-r'_C = r_{S} = k_S \left(C_{\ce{C*S}} - \frac{P_P C_{\ce{B*S}}}{K_S} \right)$

$k_S$ : small
$k_A$ : large or $r_{AD}/k_{A} \approx 0$
$k_D$ : large or $r_{D}/k_{D} \approx 0$

From Adsorption reaction

$\ce{C*S} = K_C P_C C_V$

From Desorption reaction

$\ce{B*S} = K_B P_B C_V$

From site balance

$C_V = \frac{C_t}{1 + K_B P_B + K_C P_C}$

Therefore,

$r_S = \frac{k_S K_C C_t \left( P_C - \frac{P_B P_P}{K_B} \right)}{1 + K_B P_B + K_C P_C}$

At t = 0

$-r'_{C,0} = r_S = \frac{k P_{C,0}}{1 + K_C P_{C,0}}; \qquad k = k_S K_C C_t$

At low partial pressure of C we have $1 \gg K_C P_{C,0}$

$-r'_{C,0} = k P_{C,0}$

Initial rate increases linearly with the partial pressure of C

At high initial partial pressure of C we have $K_C P_{C,0} \gg 1$

$-r'_{C,0} = k/ k_C$

Initial rate is constant.

Case 3: Desorption of Benzene the Rate-Limiting

$-r'_C = r_{D} = k_D \left( C_{\ce{B*S}} - K_B P_B C_V \right)$

$k_D$ : small
$k_A$ : large or $r_{AD}/k_{A} \approx 0$
$k_S$ : large or $r_{S}/k_{S} \approx 0$

From adsorption reaction

$C_{\ce{C*S}} = K_C P_C C_V$

From surface reaction

$C_{B,S} = K_S \left( \frac{C_{C,S}}{P_P} \right)$

From site balance

$C_V = \frac{C_t}{1 + K_C K_S \frac{P_C}{P_P} + K_C P_C}$

Therefore reaction rate:

$-r'_{C,0} = r_D = k_D K_C K_S C_t \left( \frac{P_C - \frac{P_B P_P}{K_P}} {P_P + K_C K_S P_C + K_C P_P P_C} \right)$

At t = 0; $-r'_{C,0} = k_D C_t = constant$

Initial rate is constant.

Rate law for catalytic reaction

Find the reaction rate law of the reaction

$\ce{ SO2 + 1/2 O2 -> SO3 }$

Solution

Reaction: $\ce{ SO2 + 1/2 O2 -> SO3 }$

Mechanism:

Oxygen adsorption (V is vacant site):

$\ce{ O2 + 2 V <=>[k_1][k_{-1}] 2 O*V }$

Surface reaction:

$\ce{O*V + SO2 <=>[k_2][k_{-2}] SO3 + V}$

Reaction rates:

Reaction 1: $r_1 = k_1 P_{O_2} C_V^2 - k_{-1} C_{\ce{O*V}}^2$

Reaction 2:

$r_2 = k_2 C_{\ce{O*V}} P_{\ce{SO2}} - k_{-2} P_{\ce{SO3}} C_V$

Assume reaction 2 is slow (rate limiting step)

Therefore, $r_1/ k_1 \approx 0$

$\therefore C_{\ce{O*V}}^2 = K_1 P_{\ce{O2}} C_V^2$

Rate for reaction 2 then becomes:

$r_2 = k_2 \left(K_1 P_{O_2}\right)^{1/2} C_V P_{SO_2} - k_{-2} P_{SO_3} C_V$

Site balance:

$C_t = C_V + C_{S,O} = C_V + K_1^{1/2} P_{O_2}^{1/2} C_V$

$C_V = \frac{C_t}{1 + (K_1 P_{O_2})^{1/2}}$

Substituting in equation for $r_2$

$r_2 = \frac{k_2 \left(K_1 P_{O_2}\right)^{1/2} P_{SO_2} C_t}{1 + \left(K_1 P_{O_2}\right)^{1/2}} - \frac{k_{-2} P_{SO_3} C_t}{1 + \left(K_1 P_{O_2}\right)^{1/2}}$

$r_2 = \frac{k_2 C_t P_{SO_2} \left(K_1 P_{O_2}\right)^{1/2} - k_{-2} C_t P_{SO_3}} {1 + \left(K_1 P_{O_2}\right)^{1/2}}$

at t = 0

$r_{2,0} = \frac{k_2 C_t P_{SO_2} \left(K_1 P_{O_2}\right)^{1/2}}{1 + \left(K_1 P_{O_2}\right)^{1/2}}$

Compare with the experimental data

Differential reactor
Measureable data
Keep $P_{\ce{SO2}}$ constant, change $P_{\ce{O2}}$
Keep $P_{\ce{O2}}$ constant, change $P_{\ce{SO2}}$

Surface reaction limiting reaction

The reaction $\ce{ A + B <=> C + D }$ is carried out over a solid catalyst, the reaction mechanism is believed to be

$\begin{gathered} \ce{A + S <=> A.S} \\ \ce{B + S <=> B.S} \\ \ce{A.S + B.S <=> C.S D.S} \\ \ce{C.S <=> C + S} \\ \ce{D.S <=> D + S} \end{gathered}$

Assuming step 3 is the slowest step, derive the rate law for the reaction.

Solution

Reaction: $\ce{ A + B <=> C + D }$

Mechanism:

Adsorption:

$\ce{ A + S <=>[k_1][k_{-1}] A*S }$

$\ce{ B + S <=>[k_2][k_{-2}] B*S }$

Surface reaction:

$\ce{A*S + B*S <=>[k_3][k_{-3}] C*S + D*S}$

Desorption:

$\ce{ C*S <=>[k_4][k_{-4}] C + S }$

$\ce{ D*S <=>[k_5][k_{-5}] D + S }$

Reaction rates:

$\begin{aligned} r_1 &= k_1 P_A C_V - k_{-1} C_{A \cdot S} \\ r_2 &= k_2 P_B C_V - k_{-2} C_{B \cdot S} \\ r_3 &= k_3 C_{A \cdot S} C_B \cdot S - k_{-3} C_{C \cdot S} C_{D \cdot S} \\ r_4 &= k_4 C_{C \cdot S} - k_{-4} P_C C_V \\ r_5 &= k_5 C_{D \cdot S} - k_{-5} P_D C_V \end{aligned}$

and

$\begin{aligned} K_1 &= \frac{k_1}{k_{-1}} \\ K_2 &= \frac{k_2}{k_{-2}} \\ K_3 &= \frac{k_3}{k_{-3}} \\ K_4 &= \frac{k_4}{k_{-4}} \\ K_5 &= \frac{k_5}{k_{-5}} \end{aligned}$

Assume surface reaction is rate limiting

$r_3 = k_3 C_{A \cdot S} C_{B \cdot S} - k_{-3} C_{C \cdot S} C_{D \cdot S}$

We need to eliminate $C_{A \cdot S}, C_{B \cdot S}, C_{C \cdot S}, \text{ and } C_{D \cdot S}$

$\begin{aligned} C_{A \cdot S} &= K_1 P_A C_V \\ C_{B \cdot S} &= K_2 P_B C_V \\ C_{C \cdot S} &= K_3 P_C C_V \\ C_{D \cdot S} &= K_4 P_D C_V \end{aligned}$

and $r = k_3 K_1 K_2 P_A P_B C_V^2 - k_{-3} K_4 K_5 P_C P_D C_V^2$

Write site balance to calculate $C_V$ :

$C_t = C_V + C_{A \cdot S} + C_{B \cdot S} + C_{C \cdot S} + C_{D \cdot S}$

$C_V = \frac{C_t}{1 + K_1 P_A + K_2 P_B + K_3 P_C + K_4 P_D}$

Substituting

$r = r_3 = \frac{k_3 K_1 K_2 P_A P_B C_t^2 - k_{-3} K_4 K_5 P_C P_D C_t^2} {\left(1 + K_1 P_A + K_2 P_B + K_3 P_C + K_4 P_D\right)^2}$

Initial rates in differential reactor

at t = 0 $P_C, P_D = 0$

$r_0 = \frac{k_3 K_1 K_2 P_A P_B C_t}{1 + K_1 P_A + K_2 P_B}$

Citation

BibTeX citation:

@online{utikar2024,
  author = {Utikar, Ranjeet},
  title = {In Class Activity: {Reaction} Mechanisms and Catalysis},
  date = {2024-03-23},
  url = {https://cre.smilelab.dev/content/notes/08-reaction-mechanisms-and-catalysis/in-class-activities.html},
  langid = {en}
}

For attribution, please cite this work as:

Utikar, Ranjeet. 2024. “In Class Activity: Reaction Mechanisms and Catalysis.” March 23, 2024. https://cre.smilelab.dev/content/notes/08-reaction-mechanisms-and-catalysis/in-class-activities.html.