In class activity: Non-isothermal reactor design

Lecture notes for chemical reaction engineering

Author

Ranjeet Utikar

Published

April 1, 2024

Modified

May 10, 2024

Heat of reaction

Calculate the heat of reaction for the synthesis of ammonia from hydrogen and nitrogen at 150 °C in kcal/mol of N2 reacted and also in kJ/mol of H2 reacted.

\ce{N2 + 3H2 -> 2NH3}

The enthalpy of formation of ammonia at 25 °C is H_{NH_3}^\circ (T_R) = -11020 \ cal/(mol\ \ce{NH3})

The enthalpy of formations at 25 °C

H_{NH_3}^\circ (T_R) = -11020 \ cal/(mol\ \ce{NH3})

H_{N_2}^\circ (T_R) = 0 \ cal/(mol\ \ce{NH3})

H_{H_2}^\circ (T_R) = 0 \ cal/(mol\ \ce{NH3})

Heats of formation of pure components are 0.

\Delta H_{Rx}^\circ(T_R) = \sum_{i=1}^{N} \nu_i H_i^\circ (T_R)

\Delta H_{Rx}(T) = \Delta H_{Rx}^\circ(T_R) + \Delta C_{P}(T - T_R)

Getting the C_{P} values from Perry’s handbook (Green and Southard (2019))

C_{P_{H_2}} = 6.992 cal/mol\ H_2\ K; C_{P_{N_2}} = 6.984 cal/mol\ N_2\ K; C_{P_{NH_3}} = 8.92 cal/mol\ NH_3\ K

T = 150 + 273.15
TR = 25 + 273.15

hf_nh3 = -11020
hf_n2 = 0
hf_h2 = 0

# N2 + 3H2 -> 2 NH3
nu_n2 = -1
nu_h2 = -3
nu_nh3 = 2

# Getting the Cp values from Perry's handbook (@green2019)
cp_h2 = 6.992 # cal/mol H2 K
cp_n2 = 6.984 # cal/mol N2 K
cp_nh3 = 8.92 # cal/mol NH3 K

delta_h_tr = (nu_nh3 * hf_nh3) + (nu_n2 * hf_n2 + nu_h2 * hf_h2)
delta_cp = (nu_nh3 * cp_nh3) + (nu_n2 * cp_n2 + nu_h2 * cp_h2)

delta_h = delta_h_tr + delta_cp * (T - TR)

cal = 4.184 # J
delta_h_kj = cal * delta_h_tr + delta_cp * (T - TR)

\Delta H_{Rx}^\circ(T_R) = -22.04 kcal/mol\ N_2\ reacted

\Delta H_{Rx}(T) at 423.15 K = -93.48 kJ/mol\ N_2\ reacted

\Delta H_{Rx}(T)|_{H_2} = \frac{\nu_{N_2}}{\nu_{H_2}} \Delta H_{Rx}(T)|_{N_2}

\Delta H_{Rx}(T) at 423.15 K = -31.16 kJ/mol\ H_2\ reacted

Adiabatic Liquid-Phase Isomerization of Normal Butane

Normal butane, C_4H_{10}, is to be isomerized to isobutane in a plug-flow reactor. Isobutane is a valuable product that is used in the manufacture of gasoline additives. For example, isooctane can be further reacted to form iso-octane. The 2014 selling price of n-butane was $1.5/gal, while the trading price of isobutane was $1.75/gal.

This elementary reversible reaction is to be carried out adiabatically in the liquid phase under high pressure using essentially trace amounts of a liquid catalyst that gives a specific reaction rate of 31.1 \, \text{h}^{-1} at 360 \, K. The feed enters at 330 \, K.

  1. Calculate the PFR volume necessary to process 100,000 \, \text{gal/day} (163 \, \text{kmol/h}) at 70\% conversion of a mixture 90 \, \text{mol \%} \, n-butane and 10 \, \text{mol \%} \, i-pentane, which is considered an inert.

  2. Plot and analyze X, X_e, T_r, and -r_A down the length of the reactor.

  3. Calculate the CSTR volume for 40\% conversion.

Additional information:

\Delta H^{\circ}_{Rx} = -6900 \, \text{J/mol} \, n-butane,

Activation energy = 65.7 \, \text{kJ/mol}

K_c = 3.03 at 60°C,

C_{A0} = 9.3 \, \text{mol/dm}^3 = 9.3 \, \text{kmol/m}^3

Butane: C_{P_{n-B}} = 141 \, J/mol \cdot K; C_{P_{i-B}} = 141 \, J/mol \cdot K

i-Pentane: C_{P_{i-P}} = 161 \, J/mol \cdot K

PFR algorithm

  1. Mole balance

F_{A0} \frac{dX}{dV} = -r_A \tag{1}

  1. Rate law

-r_A = k \left( C_A - \frac{C_B}{K_C}\right) \tag{2}

k = k(T_1) \exp \left[ \frac{E}{R} \left( \frac{1}{T_1} - \frac{1}{T}\right)\right] \tag{3}

K_C = K_C(T_2) \exp \left[ \frac{\Delta H_{Rx}}{R} \left( \frac{1}{T_2} - \frac{1}{T}\right)\right] \tag{4}

  1. Stoichiometry

C_A = C_{A0} (1 - X) \tag{5}

C_B = C_{A0} X \tag{6}

  1. Energy balance

\dot Q - \dot W_s - F_{A0} \sum_{i=1}^{N} \Theta_i C_{P_i} \left[ T_{i} - T_{i0}\right] - \Delta H_{Rx} F_{A0} X = 0 \tag{7}

From problem statement:

Adiabatic: \dot Q = 0

No work: \dot W_s = 0

\Delta C_{P} = C_{P_A} - C_{P_B} = 141 - 141 = 0

Substituting in Equation 7

T = T_0 + \frac{ \left( -\Delta H^\circ_{Rx} \right) X_{EB}}{\sum \Theta_i C_{Pi}} \tag{8}

  1. Solve

Solve equations 1 to 7 simultaneously.

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

# Constants
K0 = 31.1 # 1/h
T_K0 = 360 # K

KC0 = 3.3
T_KC0 = 60 + 273.15 # K

E = 65700 # J/mol 
R = 8.314 # J/mol K

DELTAHR = -6900 # J/mol

def adiabatic_pfr( V, y, *args ):

  X = y[0]
  (fa0,ca0, T0, theta, cp) = args

  sum_cp =  np.sum(theta * cp)

  T = T0 + (-DELTAHR) * X / sum_cp

  k = K0 * np.exp((E/R) * (1/T_K0 - 1/T))
  Kc = KC0 * np.exp((DELTAHR/R) * (1/T_KC0 - 1/T))

  ca = ca0 * ( 1 - X )
  cb = ca0 * X

  rate = k * (ca - cb/Kc)

  dXdV = rate/fa0

  return dXdV

# Problem data
ya0 = 0.9
yi0 = 0.1
fa = 163.0 # kmol/h
fa0 = ya0 * fa 
ca0 = 9.3   # kmol/m3

T0 = 330 # K

# n-butane = comp 1; i-butane = comp 2; i-Pentane = component 3

theta = np.array([1, 0, yi0/ya0])
cp = np.array([141, 141, 161])
                 
# Initial condition
y0 = [0]
args = (fa0, ca0, T0, theta, cp)
v_final = 5
sol = solve_ivp(adiabatic_pfr, [0, v_final], y0, args=args, dense_output=True)

v = np.linspace(0,v_final, 1000)
x = sol.sol(v)[0]

pfr_07 = v[np.argmax(x > 0.7)]

PFR volume required to obtain a conversion of 0.7 = 2.24 m^3.

# recalculate other quantities for plotting
sum_cp =  np.sum(theta * cp)
T = T0 + (-DELTAHR) * x / sum_cp
Kc = KC0 * np.exp((DELTAHR/R) * (1/T_KC0 - 1/T))
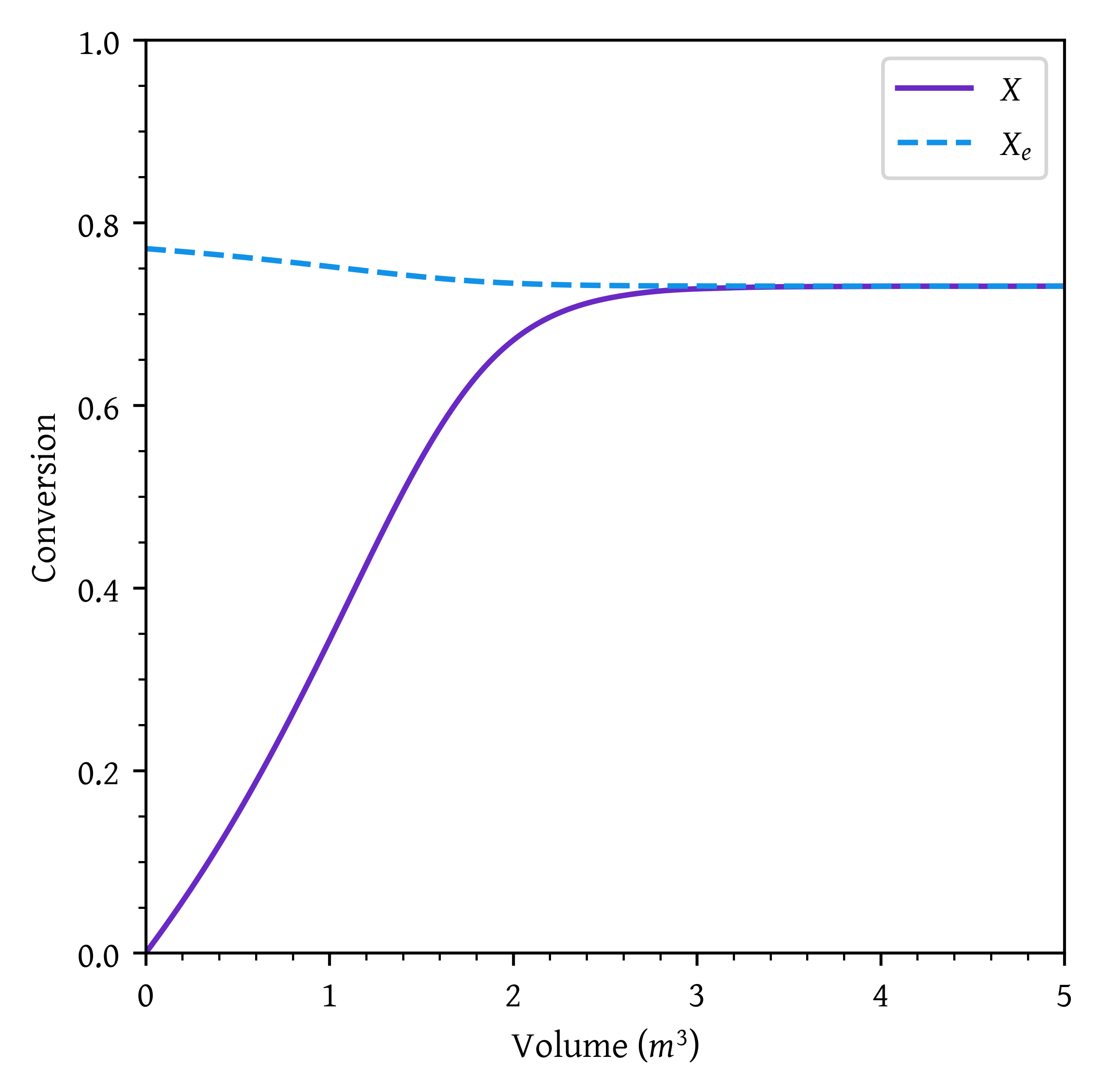
xe = Kc/(1 + Kc)

Temperature profile

plt.plot(v,T, label='Temperature')

plt.xlabel('Volume ($m^3$)')
plt.ylabel('Temperature (K)')

plt.xlim(0,v_final)
plt.ylim(T0,)

plt.show()
Figure 1: Temperature profile

Conversion profile

plt.plot(v,x, label='$X$')
plt.plot(v,xe, label='$X_e$')

plt.xlabel('Volume ($m^3$)')
plt.ylabel('Conversion')

plt.xlim(0,v_final)
plt.ylim(0,1)

plt.legend()
plt.show()
Figure 2: Conversion profile

CSTR volume

pfr_04 = v[np.argmax(x > 0.4)]

temp_04 = T[np.argmax(x > 0.4)]
kc_04 = Kc[np.argmax(x > 0.4)]
k_04 = K0 * np.exp((E/R) * (1/T_K0 - 1/temp_04))

ca = ca0 * ( 1 - 0.4 )
cb = ca0 * 0.4
rate = k_04 * (ca - cb/kc_04)

cstr_04 = fa0 * 0.4/ rate

PFR volume required to obtain a conversion of 0.4 = 1.14 m^3.

CSTR volume required to obtain a conversion of 0.4 = 0.97 m^3.

Adiabatic Equilibrium Temperature

For the elementary liquid-phase reaction

\ce{A <=> B}

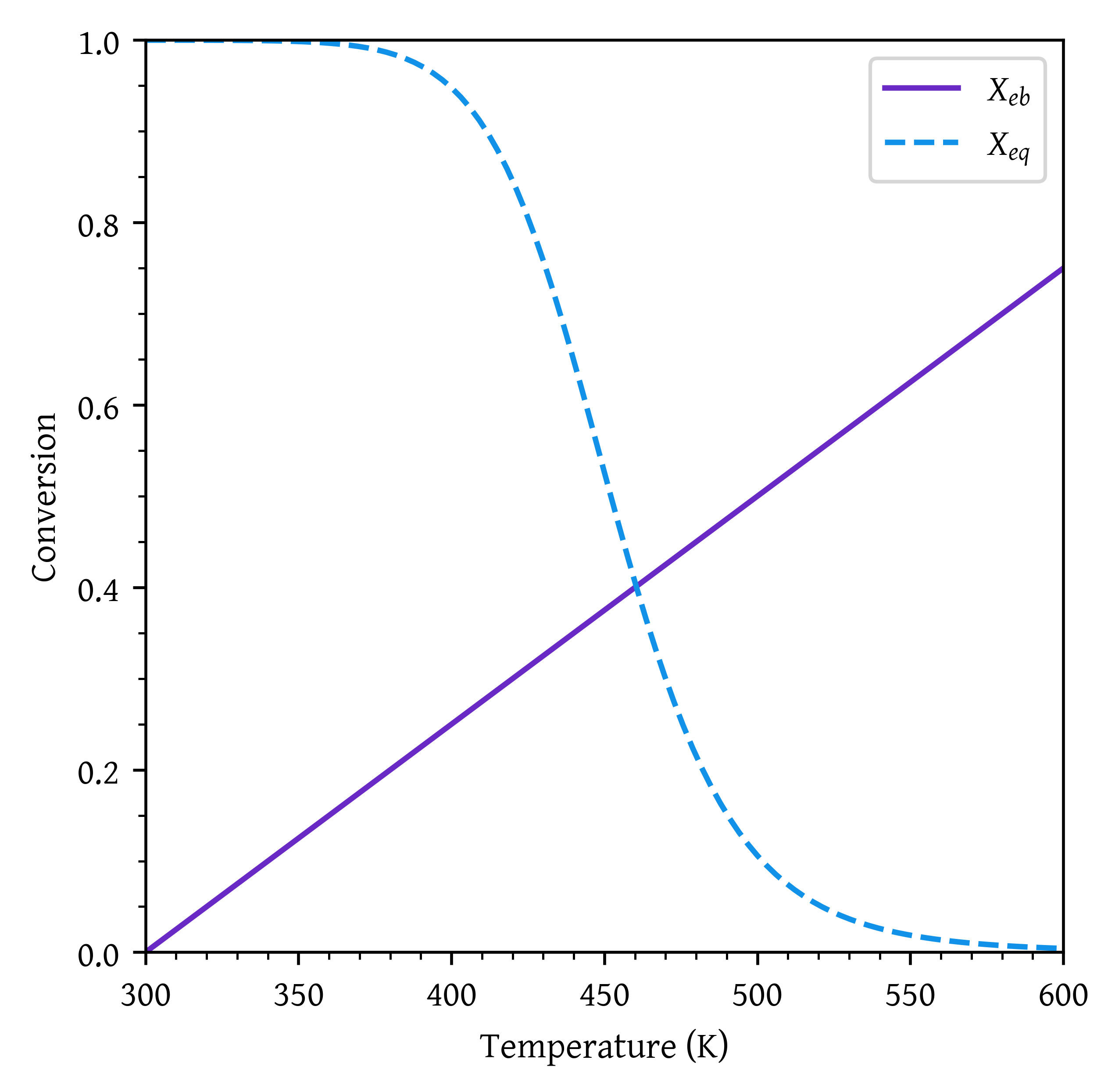
Make a plot of equilibrium conversion as a function of temperature.

  1. Combine the rate law and stoichiometric table to write -r_A as a function of k, C_{A0}, X, and X_e.

  2. Determine the adiabatic equilibrium temperature and conversion when pure A is fed to the reactor at a temperature of 300 K.

  3. What is the CSTR volume to achieve 90% of the adiabatic equilibrium conversion for \dot{v}_0 = 5 \, \text{dm}^3/\text{min}?

Additional information:†

H_A^\circ(298 \, K) = -40,000 \, \text{cal/mol}

H_B^\circ(298 \, K) = -60,000 \, \text{cal/mol}

C_{P,A} = 50 \, cal/mol \cdot K

C_{P,B} = 50 \, cal/mol \cdot K

K_c = 100,000 at 298 K, k = 10^{-3} \exp \left( \frac{E}{R} \left( \frac{1}{298} - \frac{1}{T} \right) \right) \text{min}^{-1} with E = 10,000 \, \text{cal/mol}

  1. Rate law

-r_A = k \left( C_A - \frac{C_B}{K_C}\right) \tag{9}

k = k(T_1) \exp \left[ \frac{E}{R} \left( \frac{1}{T_1} - \frac{1}{T}\right)\right] \tag{10}

K_C = K_C(T_2) \exp \left[ \frac{\Delta H_{Rx}}{R} \left( \frac{1}{T_2} - \frac{1}{T}\right)\right] \tag{11}

  1. Equilibrium

K_e = \frac{C_{Be}}{C_{Ae}} \tag{12}

  1. Stoichiometry

C_A = C_{A0} (1 - X) \tag{13}

C_B = C_{A0} X \tag{14}

Combining Equation 9, Equation 12, Equation 13, and Equation 14

X_e = \frac{K_e(T)}{1 + K_e(T)} \tag{15}

  1. Energy balance

\dot Q - \dot W_s - F_{A0} \sum_{i=1}^{N} \Theta_i C_{P_i} \left[ T_{i} - T_{i0}\right] - \Delta H_{Rx} F_{A0} X = 0 \tag{16}

From problem statement:

Adiabatic: \dot Q = 0

No work: \dot W_s = 0

\Delta C_{P} = C_{P_A} - C_{P_B} = 141 - 141 = 0

Substituting in Equation 16

X_{EB} = \frac { \sum \Theta_i C_{P_i} \left[ T_{i} - T_{0}\right] } {- \Delta H_{Rx}^\circ (T_R) } \tag{17}

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
from scipy.optimize import fsolve

# Constants
HF_A = -40000 # cal/mol
HF_B = -60000 # cal/mol

CP_A = 50 # cal/mol K
CP_B = 50 # cal/mol K

# A <-> B
D_CP = CP_B - CP_A

KE0 = 100000
T_KE0 = 298 # K

K0 = 1e-3 # 1/h
T_K0 = 298 # K

E = 10000  # cal/mol
R = 1.987 # cal/mol K

DELTAHR = HF_B - HF_A

T0 = 300 # K

Ke = lambda T: KE0 * np.exp((DELTAHR/R) * (1/T_KE0 - 1/T))
Xe = lambda T: Ke(T)/(1 + Ke(T))
Xeb = lambda T, T0: CP_A * (T - T0)/(-DELTAHR)

intersect = lambda T: Xe(T) - Xeb(T, T0)

sol = fsolve(intersect, T0)

T_adiab = sol[0]
X_eadiab = Xe( T_adiab )

Adiabatic equilibrium temperature = 460.40 K.

Adiabatic equilibrium conversion = 0.40.

T_final = T0 + 300
temperatures = np.linspace(T0, T_final , 100)
conv_eb = Xeb(temperatures, T0)
conv_eq = Xe(temperatures)

plt.plot(temperatures,conv_eb, label="$X_{eb}$")
plt.plot(temperatures,conv_eq, label="$X_{eq}$")

plt.xlabel('Temperature (K)')
plt.ylabel('Conversion')

plt.xlim(T0, T_final)
plt.ylim(0,1)
plt.legend()
plt.show()
Figure 3: Conversion vs. temperatures

CSTR Volume

V = \frac{F_{A0} X}{ -r_A } \tag{18}

Calculate temperature corresponding to X = 0.9 Xe

T = T_0 + \frac{ \left( -\Delta H^\circ_{Rx} \right) X_{EB}}{\sum \Theta_i C_{Pi}} \tag{19}

Calculate rate at this temperature using Equation 9 and Equation 10.

k = lambda T: K0 * np.exp((E/R) * (1/T_K0 - 1/T))

v_0 = 5 # dm^3/min
x_cstr = 0.9 * X_eadiab

def v_cstr(x, xin, t0, ca0, v_0):
  t_cstr = t0 + (x - xin)*(-DELTAHR)/CP_A
  rate = k(t_cstr) * ca0 * (1 - (x/Xe(t_cstr)))
  v_cstr = v_0 * ca0 * x/rate
  return v_cstr,t_cstr

V_cstr,T_cstr = v_cstr(x_cstr,0,T0,1.0,v_0)

For a CSTR to achieve a conversion of 90% of X_e (= 0.36), volume required is 17.57 dm^3. The CSTR operates at 444.36 K.

Interstage Cooling for Highly Exothermic Reactions

What conversion could be achieved in the previous example if two interstage coolers that had the capacity to cool the exit stream to 350 K were available? Also, determine the heat duty of each exchanger for a molar feed rate of A of 40 mol/s. Assume that 95% of the equilibrium conversion is achieved in each reactor. The feed temperature to the first reactor is 300 K.

# Stage 1

fa0 = 40.0 # mol/s

x1 = 0.95 * X_eadiab
v_cstr1, t_cstr1 = v_cstr(x1,0,T0,1.0,v_0)

Stage 1: X_{1} = 0.38. V_{CSTR} = 25.69 dm^3. T_{CSTR} = 452.38 K.

Heat Load:

\dot Q - \dot W_s - \sum F_{i} C_{P_i}(T_2 - T_1) = 0 \tag{20}

\dot W_s = 0; C_{P_A} = C_{P_B}

\dot Q = (F_{A} + F_B) C_{P_A}(T_2 - T_1) \tag{21}

T_ic = 350
qdot1 = fa0 * CP_A * (T_ic - t_cstr1)

Stage 1 cooling requirement : \dot Q_1 = -204.76 kcal/s.

# Stage 2
# find adiabatic conversion and temperature for second stage

intersect = lambda T: Xe(T) - ( x1 + Xeb(T, T_ic))

sol = fsolve(intersect, T0)

T2_adiab = sol[0]
X2_eadiab = Xe( T2_adiab )

x2 = X2_eadiab * 0.95

v_cstr2, t_cstr2 = v_cstr(x2,x1,T_ic,1.0,v_0)
qdot2 = fa0 * CP_A * (T_ic - t_cstr2)

Stage 2: X_{2} = 0.58. T_{adiab,2} = 442.93 K. V_{CSTR,2} = 71.24 dm^3. T_{CSTR,2} = 430.66 K.

Stage 2 cooling requirement : \dot Q_2 = -161.33 kcal/s.

# Stage 3
# find adiabatic conversion and temperature for second stage

intersect = lambda T: Xe(T) - ( x2 + Xeb(T, T_ic))

sol = fsolve(intersect, T0)

T3_adiab = sol[0]
X3_eadiab = Xe( T3_adiab )

x3 = X3_eadiab * 0.95

v_cstr3, t_cstr3 = v_cstr(x3,x2,T_ic,1.0,v_0)
qdot3 = fa0 * CP_A * (T_ic - t_cstr3)

Stage 3: X_{3} = 0.74. T_{adiab,3} = 428.03 K. V_{CSTR,3} = 195.40 dm^3. T_{CSTR,3} = 412.47 K.

Stage 3 cooling requirement : \dot Q_3 = -124.95 kcal/s.

Production of Acetic Anhydride

Jeffreys, in a treatment of the design of an acetic anhydride manufacturing facility, states that one of the key steps is the endothermic vapor-phase cracking of acetone to ketene and methane.

The reaction is as follows: \ce{ CH3COCH3 -> CH2CO + CH4}

He states further that this reaction is first-order with respect to acetone and that the specific reaction rate can be expressed by

\ln k = 34.34 - \frac{34,222}{T}

where k is in reciprocal seconds and T is in Kelvin. In this design it is desired to feed 7850 kg of acetone per hour to a tubular reactor. The reactor consists of a bank of 1000 one-inch schedule 40 tubes. We shall consider four cases of heat exchanger operation. The inlet temperature and pressure are the same for all cases at 1035 K and 162 kPa (1.6 atm) and the entering heating-fluid temperature available is 1250 K.

A bank of 1000 one-inch, schedule 40 tubes 1.79 m in length corresponds to 1.0 m³ (0.001 m³/tube = 1.0 dm³/tube) and gives 20% conversion. Ketene is unstable and tends to explode, which is a good reason to keep the conversion low. However, the pipe material and schedule size should be checked to learn if they are suitable for these temperatures and pressures. The heat-exchange fluid has a flow rate, \dot{m}_c, of 0.111 mol/s, with a heat capacity of 34.5 J/mol·K.

The cases are as follows:

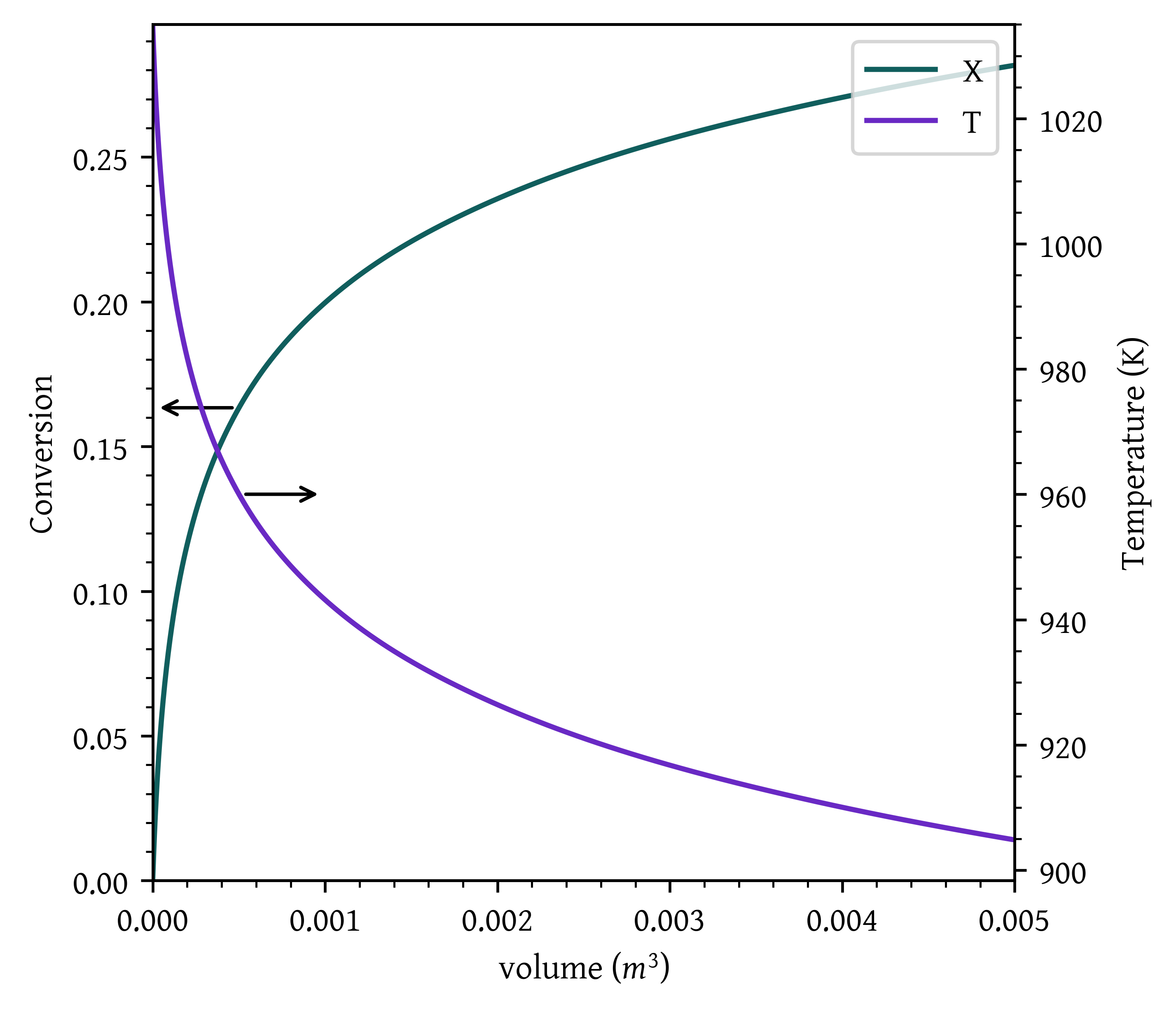
  • Case 1: The reactor is operated adiabatically.
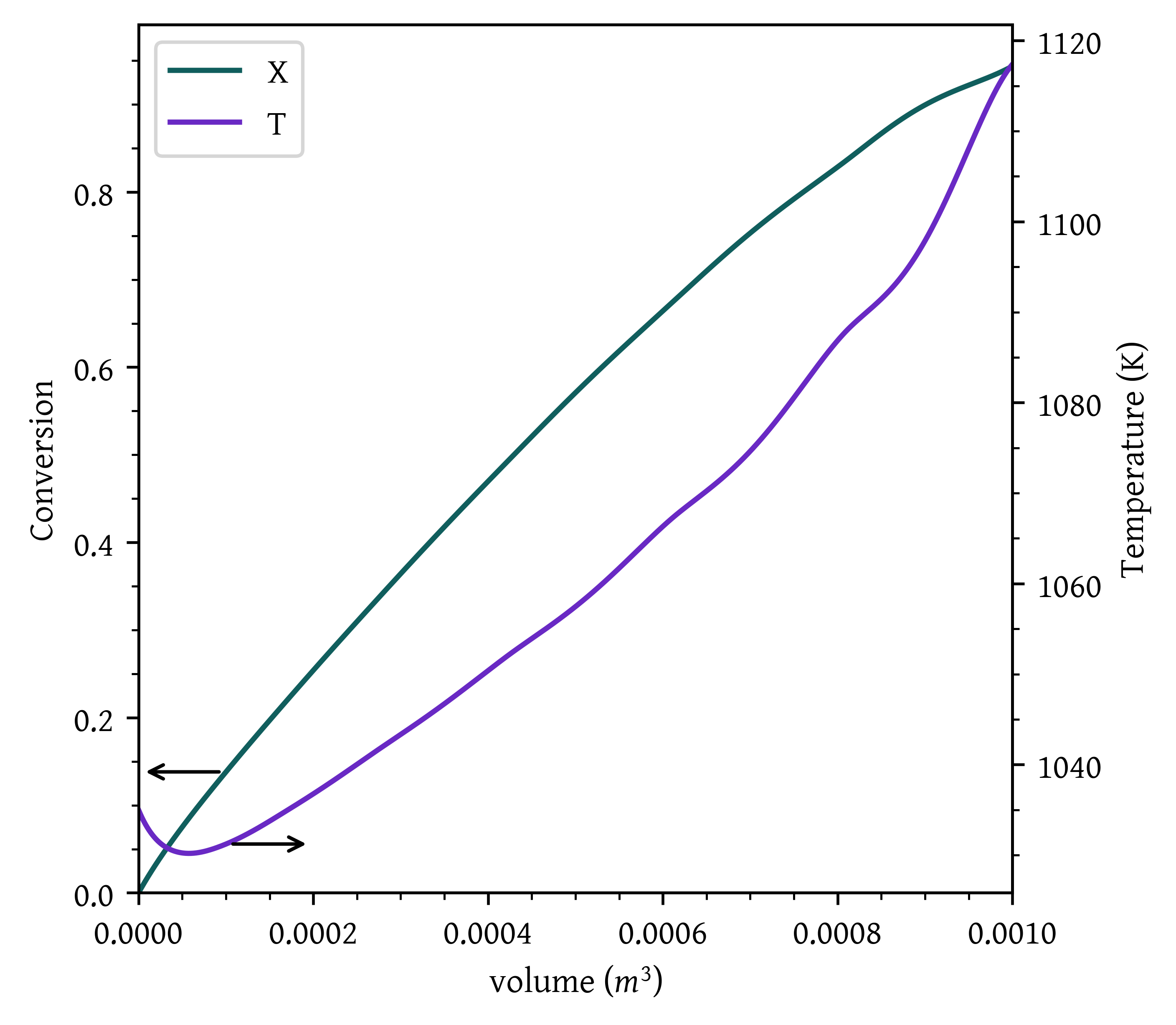
  • Case 2: Constant heat-exchange fluid temperature T_a = 1250 K.
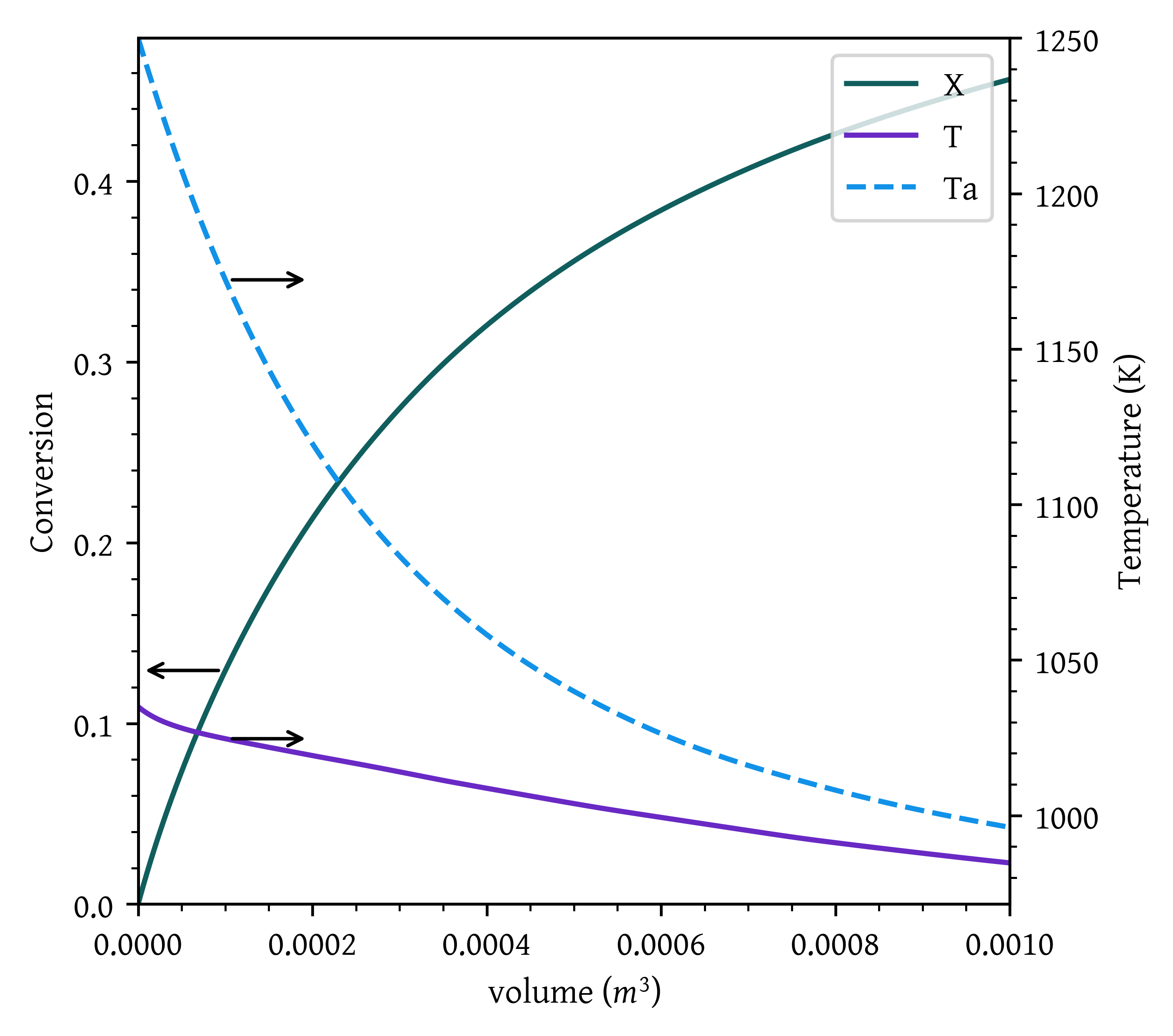
  • Case 3: Co-current heat exchange with T_{a0} = 1250 K.
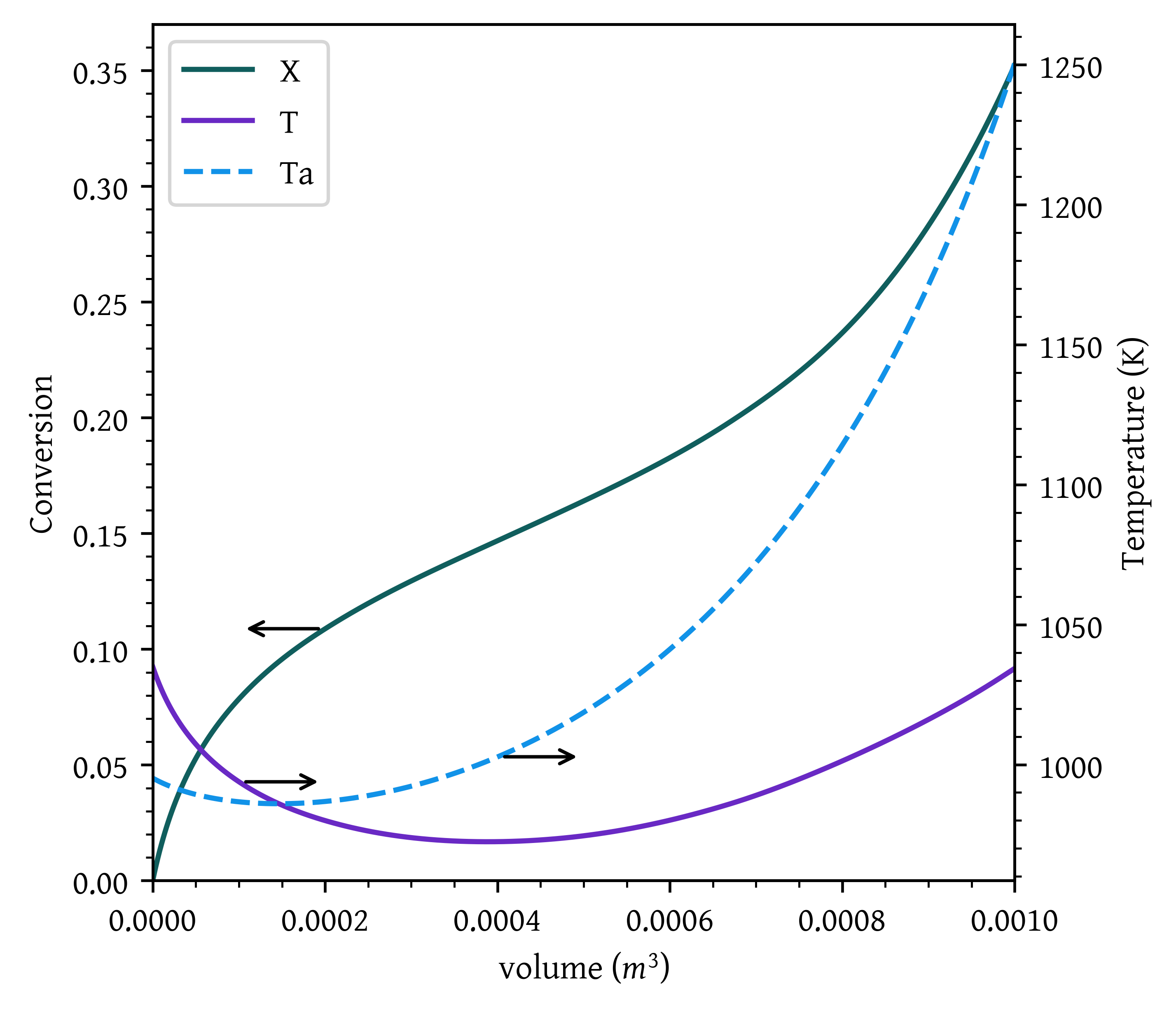
  • Case 4: Countercurrent heat exchange with T_{a0} = 1250 K.

Additional information:

  • For acetone (A): \Delta H^{\circ}_{A}(T_R) = -216.67 kJ/mol, C_{p,A} = 163 J/mol·K
  • For ketene (B): \Delta H^{\circ}_{B}(T_R) = -61.09 kJ/mol, C_{p,B} = 83 J/mol·K
  • For methane (C): \Delta H^{\circ}_{C}(T_R) = -74.81 kJ/mol, C_{p,C} = 71 J/mol·K

The overall heat transfer coefficient Ua = 110 J/s \cdot m^3 \cdot K.

Reaction: \ce {A -> B + C}

  1. Mole balance

\frac{dX}{dV} = -\frac{r_A}{F_{A0}}

  1. Rate law

-r_A = k C_A

  1. Stoichiometry C_A = \frac{ C_{A0} (1 - X) }{ (1 + \epsilon X) } \frac{ T_0 }{ T }

  2. Energy balance

Reactor balance

\frac{dT}{dV} = \frac{ U a (T_a - T) + r_A \left[ \Delta H_{Rx}^\circ+ \Delta C_P (T - T_R)\right] }{ F_{A0} \left( \sum \Theta_i C_{P_i} + X \Delta C_P \right) }

Heat exchanger

\frac{dT_a}{dV} = \frac{ U a (T - T_a) }{ \dot m_C C_{P_C} } 

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

# Constants
R = 8.314 # J/mol K
TR = 298 # K
# Components: 1: A(acetone), 2: B(ketene), 3: C(methane)
HF = np.array ([-216.67, -61.09, -74.81])*1000   # J/mol
CP = np.array ([163.0, 83.0, 71.0]) # J/mol K
MW = np.array ([58.0, 42.0, 20.0]) # g/mol

k = lambda t: np.exp( 34.34 - 34222/t )
# k = lambda t: 3.58 * np.exp( 34222 * (1/1035 - 1/t))

def pfr (v, x, *args):
  X, T, Ta = x
  (fa0, ca0, T0, epsilon, delta_hr_tr, delta_cp, theta, UA, mc, cpc) = args

  ca = ca0 * (( 1 - X ) / ( 1 + epsilon * X )) * (T0/T)
  rate = k(T) * ca # -r_A
  delta_h = delta_hr_tr + delta_cp * (T - TR)

  dxdv = rate/fa0
  dtdv = (UA * ( Ta - T ) + (-rate * delta_h))/( fa0 * ( np.sum(theta * CP) + X * delta_cp) )
  dtadv = UA * ( T - Ta )/ (mc * cpc)

  return [dxdv, dtdv, dtadv]

# Data

nu = np.array ([-1.0, 1.0, 1.0]) # stoichiometric coefficients

f0 = 7850 # kg/h
T0 = 1035.0 # K
P0 = 162.0e3 # Pa

n_tubes = 1000
d_tube = 26.64e-3  # 1" schedule 40 pipe inner diameter mm
Ta0 = 1250 # K
a = 4/d_tube
U = 110.0 # J/s m^3 K
UA = U * a


mc = 0.111 # mol/s
cpc = 34.5 # J/mol K

# inlet mole fraction
y0 = np.array ([1.0, 0.0, 0.0])
theta = np.array([1.0, 0.0, 0.0])

fa0 = (f0 / ( y0[0] * MW[0])) / n_tubes # kmol/h
fa0 = fa0 * (1000/3600)  # mol/s

pa0 = y0[0] * P0
ca0 = pa0/(R * T0)
v_0 = fa0/ca0
ya0 = y0[0]

# Heat of reaction at 298K
delta_hr_tr = np.sum(HF * nu)
delta_cp = np.sum(CP * nu)

epsilon = ya0 * np.sum(nu)
Parameter values
\Delta H^\circ_{Rx} (T_R) = 80770.00 J/mol \Delta C_P = -9.00 J/mol\ K T_0 = 1035.00 K
F_{A0} = 3.76e-02 mol/s C_{A0} = 18.83 mol/m^3 T_R = 298.00 K
C_{P_A} = 163.00 J/mol\ K Ua = 16516.52 J/m^3\ s\ K \dot m_C = 0.11 mol/s
C_{P_C} = 34.50 J/mol\ K V_f = 0.001 m^3 
args = (fa0, ca0, T0, epsilon, delta_hr_tr, delta_cp, theta, 0, mc, cpc)

initial_conditions = np.array([0, T0, Ta0])
v_final = 0.005

sol = solve_ivp(pfr, [0, v_final], initial_conditions, args=args, dense_output=True)
v = np.linspace(0,v_final, 1000)
x = sol.sol(v)[0]
T = sol.sol(v)[1]
Ta = sol.sol(v)[2]

fig, ax1 = plt.subplots()

# Plot x on the original y-axis
plt_x = ax1.plot(v, x, color='#105e5d', label='X')
ax1.set_xlabel('volume ($m^3$)')
ax1.set_ylabel('Conversion')
ax1.set_xlim(0,v[-1])
ax1.set_ylim(0,)

# Create a second y-axis for T and Ta
ax2 = ax1.twinx()
plt_t = ax2.plot(v, T, label='T') 
# plt_ta = ax2.plot(v, Ta, label='Ta') 
ax2.set_ylabel('Temperature (K)')

ax2.set_xlim(0,v[-1])
ax2.set_ylim(top=T0)

arrow_properties = dict(arrowstyle="<-,head_length=0.7,head_width=0.25",
                        color="black")

ax1.annotate('', xy=(v[100],x[100]), xytext=(v[0], x[100]),arrowprops=dict(arrowstyle="<-"))
ax2.annotate('', xy=(v[100],T[100]), xytext=(v[200], T[100]),arrowprops=dict(arrowstyle="<-"))

# fig.tight_layout()
handles, labels = [], []
for ax in [ax1, ax2]:
    for handle, label in zip(*ax.get_legend_handles_labels()):
        handles.append(handle)
        labels.append(label)
plt.legend(handles, labels)
plt.show()

Adiabatic conversion and temperature
def pfr_const_heatex_fluid_T (v, x, *args):
  X, T, Ta = x
  (fa0, ca0, T0, epsilon, delta_hr_tr, delta_cp, theta, UA, mc, cpc) = args

  ca = ca0 * (( 1 - X ) / ( 1 + epsilon * X )) * (T0/T)
  rate = k(T) * ca # -r_A
  delta_h = delta_hr_tr + delta_cp * (T - TR)

  dxdv = rate/fa0
  dtdv = (UA * ( Ta - T ) + (-rate * delta_h))/( fa0 * ( np.sum(theta * CP) + X * delta_cp) )
  dtadv = 0.0

  return [dxdv, dtdv, dtadv]


args = (fa0, ca0, T0, epsilon, delta_hr_tr, delta_cp, theta, UA, mc, cpc)

initial_conditions = np.array([0, T0, Ta0])
v_final = 0.001

sol = solve_ivp(pfr_const_heatex_fluid_T, [0, v_final], initial_conditions, args=args, dense_output=True)
v = np.linspace(0,v_final, 1000)
x = sol.sol(v)[0]
T = sol.sol(v)[1]
Ta = sol.sol(v)[2]

fig, ax1 = plt.subplots()

# Plot x on the original y-axis
plt_x = ax1.plot(v, x, color='#105e5d', label='X')
ax1.set_xlabel('volume ($m^3$)')
ax1.set_ylabel('Conversion')
ax1.set_xlim(0,v[-1])
ax1.set_ylim(0,)

# Create a second y-axis for T and Ta
ax2 = ax1.twinx()
plt_t = ax2.plot(v, T, label='T') 
# plt_ta = ax2.plot(v, Ta, label='Ta') 
ax2.set_ylabel('Temperature (K)')

ax2.set_xlim(0,v[-1])

arrow_properties = dict(arrowstyle="<-,head_length=0.7,head_width=0.25",
                        color="black")

ax1.annotate('', xy=(v[100],x[100]), xytext=(v[0], x[100]),arrowprops=dict(arrowstyle="<-"))
ax2.annotate('', xy=(v[100],T[100]), xytext=(v[200], T[100]),arrowprops=dict(arrowstyle="<-"))

# fig.tight_layout()
handles, labels = [], []
for ax in [ax1, ax2]:
    for handle, label in zip(*ax.get_legend_handles_labels()):
        handles.append(handle)
        labels.append(label)
plt.legend(handles, labels)
plt.show()

Constant heat exchange fluid temperature: conversion and temperature
args = (fa0, ca0, T0, epsilon, delta_hr_tr, delta_cp, theta, UA, mc, cpc)

initial_conditions = np.array([0, T0, Ta0])
v_final = 0.001

sol = solve_ivp(pfr, [0, v_final], initial_conditions, args=args, dense_output=True)
v = np.linspace(0,v_final, 1000)
x = sol.sol(v)[0]
T = sol.sol(v)[1]
Ta = sol.sol(v)[2]

fig, ax1 = plt.subplots()

# Plot x on the original y-axis
plt_x = ax1.plot(v, x, color='#105e5d', label='X')
ax1.set_xlabel('volume ($m^3$)')
ax1.set_ylabel('Conversion')
ax1.set_xlim(0,v[-1])
ax1.set_ylim(0,)

# Create a second y-axis for T and Ta
ax2 = ax1.twinx()
plt_t = ax2.plot(v, T, label='T') 
plt_ta = ax2.plot(v, Ta, label='Ta') 
ax2.set_ylabel('Temperature (K)')

ax2.set_xlim(0,v[-1])
ax2.set_ylim(top=Ta0)

arrow_properties = dict(arrowstyle="<-,head_length=0.7,head_width=0.25",
                        color="black")

ax1.annotate('', xy=(v[100],x[100]), xytext=(v[0], x[100]),arrowprops=dict(arrowstyle="<-"))
ax2.annotate('', xy=(v[100],T[100]), xytext=(v[200], T[100]),arrowprops=dict(arrowstyle="<-"))
ax2.annotate('', xy=(v[100],Ta[100]), xytext=(v[200], Ta[100]),arrowprops=dict(arrowstyle="<-"))

# fig.tight_layout()
handles, labels = [], []
for ax in [ax1, ax2]:
    for handle, label in zip(*ax.get_legend_handles_labels()):
        handles.append(handle)
        labels.append(label)
plt.legend(handles, labels)
plt.show()

Cocurrent heat exchange: conversion and temperature
def pfr_countercurrent_exchange (v, x, *args):
  X, T, Ta = x
  (fa0, ca0, T0, epsilon, delta_hr_tr, delta_cp, theta, UA, mc, cpc) = args

  ca = ca0 * (( 1 - X ) / ( 1 + epsilon * X )) * (T0/T)
  rate = k(T) * ca # -r_A
  delta_h = delta_hr_tr + delta_cp * (T - TR)

  dxdv = rate/fa0
  dtdv = (UA * ( Ta - T ) + (-rate * delta_h))/( fa0 * ( np.sum(theta * CP) + X * delta_cp) )
  dtadv = - UA * ( T - Ta )/ (mc * cpc)

  return [dxdv, dtdv, dtadv]


v_final = 0.001

# This temperature needs to be guessed for Ta to be 1250 at V = V_final
Ta0 = 995.15

args = (fa0, ca0, T0, epsilon, delta_hr_tr, delta_cp, theta, UA, mc, cpc)

initial_conditions = np.array([0, T0, Ta0])

sol = solve_ivp(pfr_countercurrent_exchange, [0, v_final], initial_conditions, args=args, dense_output=True)
v = np.linspace(0,v_final, 1000)
x = sol.sol(v)[0]
T = sol.sol(v)[1]
Ta = sol.sol(v)[2]

fig, ax1 = plt.subplots()

# Plot x on the original y-axis
plt_x = ax1.plot(v, x, color='#105e5d', label='X')
ax1.set_xlabel('volume ($m^3$)')
ax1.set_ylabel('Conversion')
ax1.set_xlim(0,v[-1])
ax1.set_ylim(0,)

# Create a second y-axis for T and Ta
ax2 = ax1.twinx()
plt_t = ax2.plot(v, T, label='T') 
plt_ta = ax2.plot(v, Ta, label='Ta') 
ax2.set_ylabel('Temperature (K)')

ax2.set_xlim(0,v[-1])

arrow_properties = dict(arrowstyle="<-,head_length=0.7,head_width=0.25",
                        color="black")

ax1.annotate('', xy=(v[200],x[200]), xytext=(v[100], x[200]),arrowprops=dict(arrowstyle="<-"))
ax2.annotate('', xy=(v[100],T[100]), xytext=(v[200], T[100]),arrowprops=dict(arrowstyle="<-"))
ax2.annotate('', xy=(v[400],Ta[400]), xytext=(v[500], Ta[400]),arrowprops=dict(arrowstyle="<-"))

# fig.tight_layout()
handles, labels = [], []
for ax in [ax1, ax2]:
    for handle, label in zip(*ax.get_legend_handles_labels()):
        handles.append(handle)
        labels.append(label)
plt.legend(handles, labels)
plt.show()

Countercurrent exchange: conversion and temperature

References

Green, Don W., and Marylee Z. Southard, eds. 2019. Perry’s Chemical Engineers’ Handbook. Ninth edition, 85th anniversary edition. New York: McGraw Hill Education.

Citation

BibTeX citation:
@online{utikar2024,
  author = {Utikar, Ranjeet},
  title = {In Class Activity: {Non-isothermal} Reactor Design},
  date = {2024-04-01},
  url = {https://cre.smilelab.dev//content/notes/07-non-isothermal-reactor-design/in-class-activities.html},
  langid = {en}
}
For attribution, please cite this work as:
Utikar, Ranjeet. 2024. “In Class Activity: Non-Isothermal Reactor Design.” April 1, 2024. https://cre.smilelab.dev//content/notes/07-non-isothermal-reactor-design/in-class-activities.html.