Distribution of residence time
Chemical Reaction Engineering
General Considerations
Models developed so far are for perfectly mixed batch reactor, the plug flow tubular reactor, packed bed reactor, and perfectly mixed continuous tank reactor.
Real world behavior is often very different from the ideal behavior.
Use residence time distribution to analyze and characterize non-ideal reactors.
diagnose problems of reactor operations
predict conversion in existing reactor when new chemical reaction is used in the reactor.
Examples of non-ideality

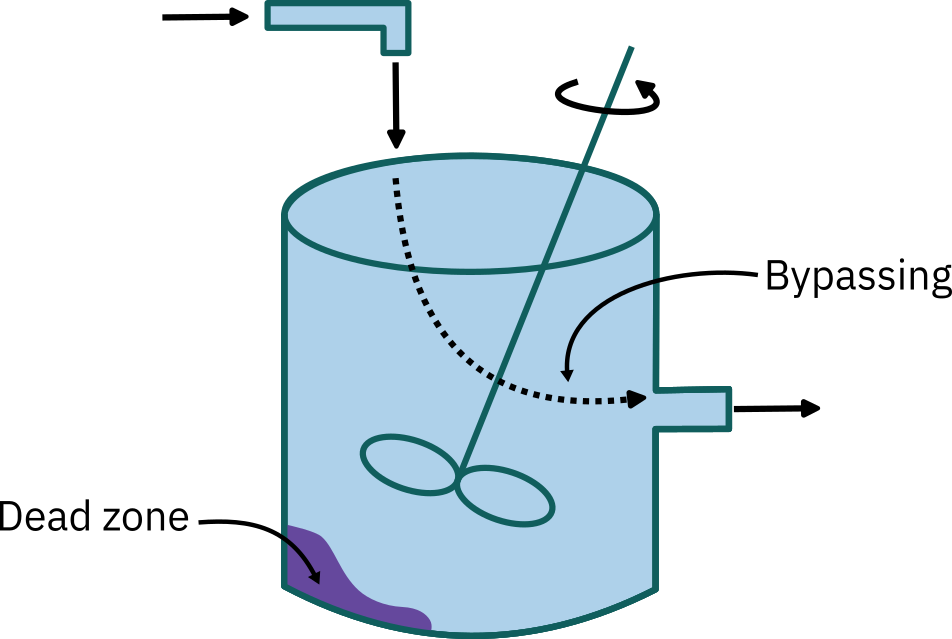
Describing deviation from ideal reactor mixing pattern
- Residence time distribution (RTD)
- Quality of mixing
- Model used to describe the system
Residence time distribution (RTD) function
Popularized by Prof. P. V. Dankwerts
Residence Time Distribution (RTD) function
Residence time: The time atoms have spent in the reactor.
Plug flow reactor: Atoms spend exactly the same time in these two reactors.
Ideal batch reactor: Atoms spend exactly the same time in these two reactors.
CSTR: Feed introduced into a CSTR becomes completely mixed with the material already in the reactor.
- Some atoms entering the CSTR leave almost immediately.
- Other atoms remain in the reactor almost forever as all the material recirculates within the reactor and is virtually never removed from the reactor at one time.
Distribution of residence times can significantly affect reactor performance.
The RTD is a characteristic of the mixing that occurs in the chemical reactor.
RTD yields distinctive clues to the type of mixing occurring within it and is one of the most informative characteristics of the reactor.
Measurement of the RTD
- Determined experimentally
- Injecting tracer into the reactor at some time t=0 and then measuring the tracer concentration C in the effluent stream as a function of time.
![]()
- Properties of Tracer
- Inert (non-reactive)
- Easily detectable
- Similar physical properties to the reacting mixture
- Completely soluble in the reacting mixture
- Does not adsorb on reactor walls
- Tracer behavior should mimic the behavior of material flowing in the reactor.
- Common tracers: colored dye, radioactive material, inert gases
Pulse input experiment
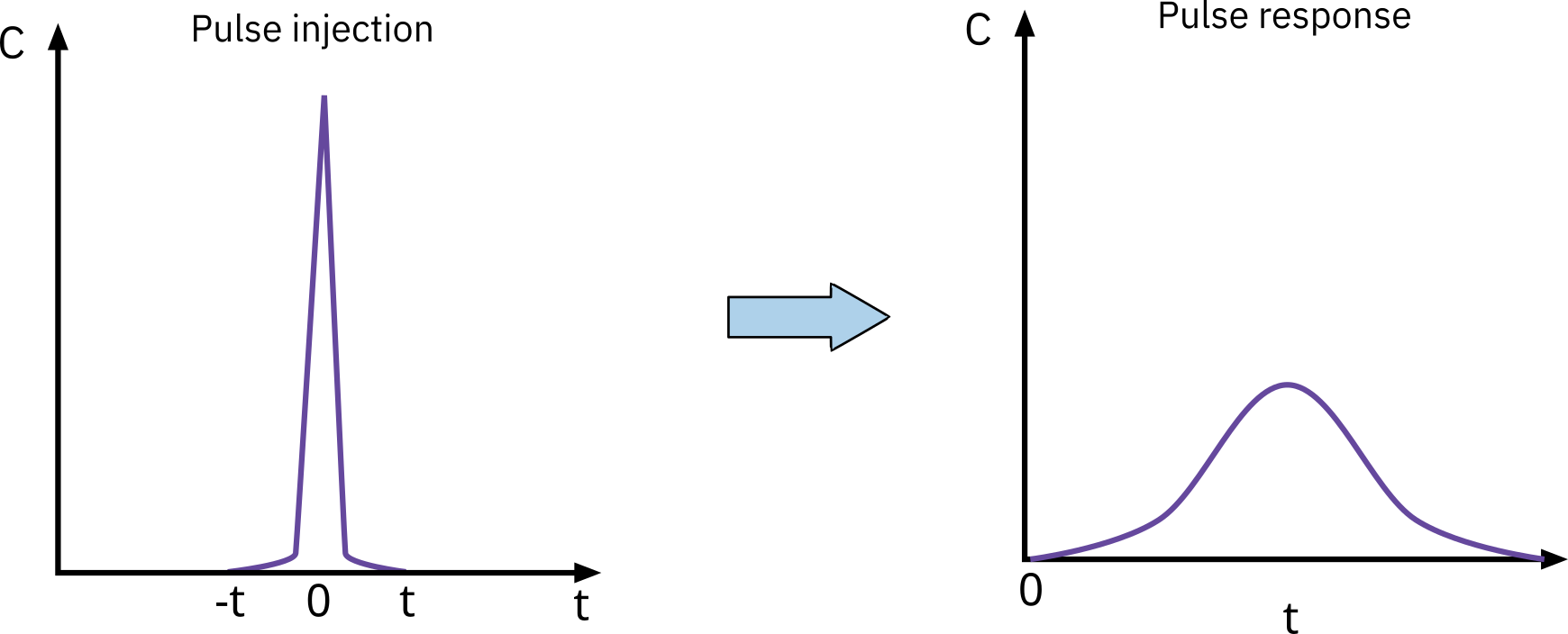
An amount of tracer N0 is suddenly injected in one shot into the feed stream.
Outlet concentration is measured with time.
Consider single-input and single-output system:
- Only flow carries the tracer material.
- No dispersion.
- Increment of time Δt is sufficiently small that the concentration of tracer C(t) exiting between t and t+Δt is essentially the same.
Amount of tracer material leaving the reactor between t and (t+Δt): ΔN=C(t)⋅υ⋅Δtwhere υ is the volumetric flow rate(1)
Pulse input experiment
- Dividing by the Total Amount of Material that was Injected
N0ΔN=N0υC(t)Δt(2)
⇒ Fraction of material that has residence time in the reactor between t and t+Δt
- For pulse injection let
E(t)=N0υC(t)... Residence time function
Residence time function
Function that describes in a quantitative manner how much time different fluid elements have spent in the reactor
∴N0ΔN=E(t)Δt
Pulse input experiment
E(t)dt is the fraction of fluid exiting the reactor that has spent between time t and t+Δt inside the reactor.
If N0 is not known directly, it can be obtained from the outlet concentration measurements by summing up all the amounts from 0 to ∞
Writing Equation 1 in Differential Form
dN=υC(t)dt
Integrating
N0=∫0∞υC(t)dt
υ is usually constant, therefore
E(t)=∫0∞C(t)dtC(t)(3)
- E(t) is also called exit age distribution function
Pulse input experiment
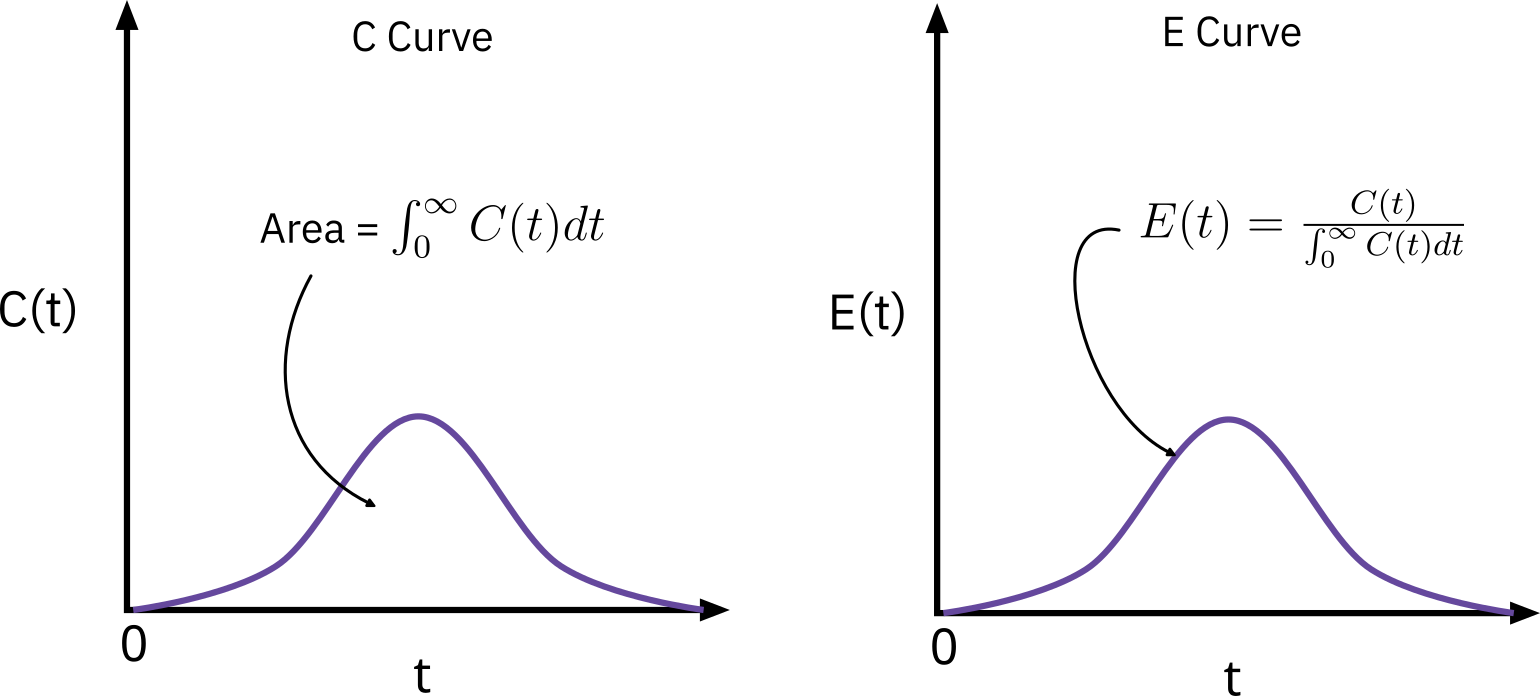
- The E curve is just the C curve divided by the area under the C curve.
Pulse input experiment
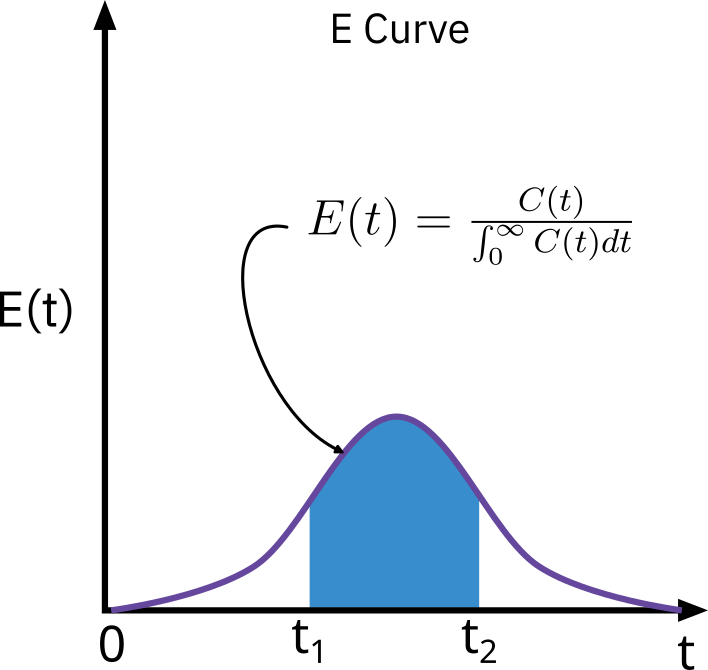
Fraction of material leaving the reactor that has resided in the reactor between t1 and t2
=∫t1t2E(t)dt
Fraction of all material that has resided for a time t in the reactor between t=0 and t=∞ is 1
∫0∞E(t)dt=1
Difficulties with pulse technique
- Obtaining a reasonable pulse at the reactor entrance
- Injection time should be very short compared to residence times in various segments of the reactor.
- There must be negligible dispersion between the point of injection and the entrance to the reactor.
- If these conditions are achieved, pulse technique is a simple and direct way to obtain RTD.
Step tracer experiment
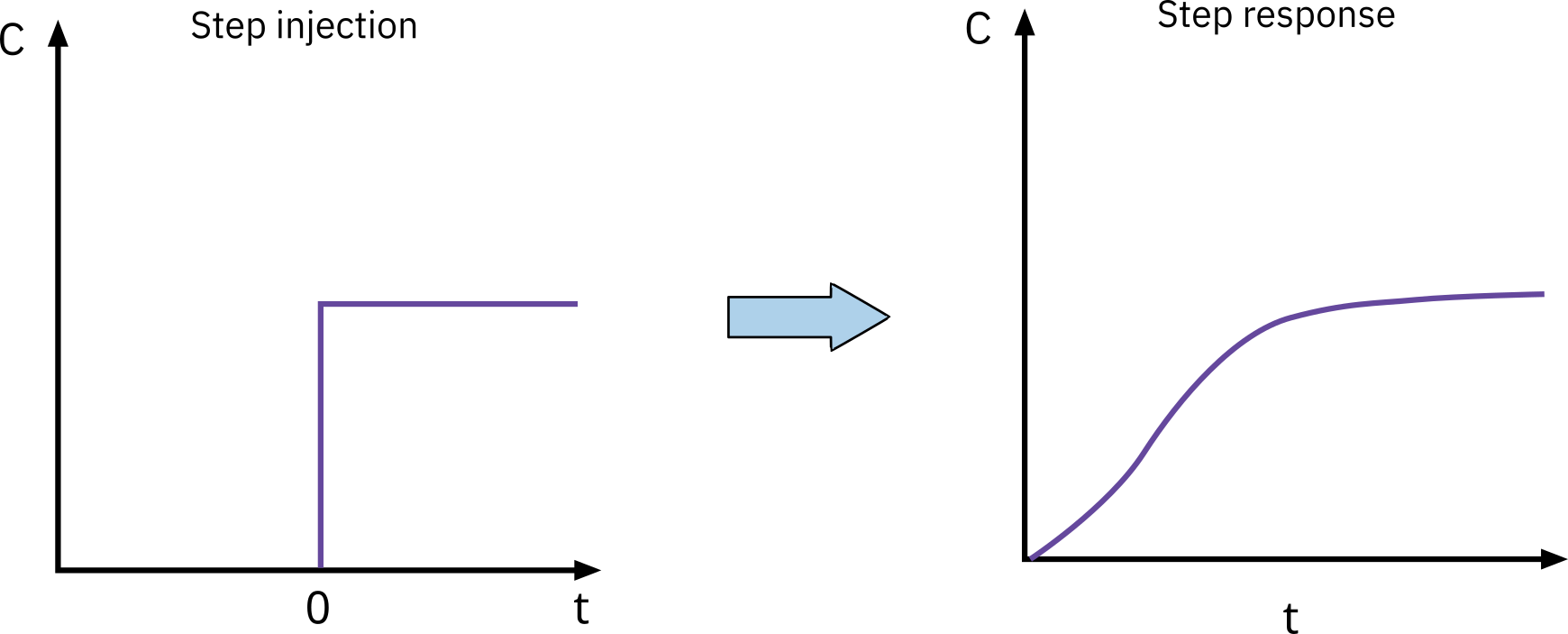
Inlet is either:
- Perfect pulse input (Dirac delta function)
- Imperfect pulse, determine E(t)
Cumulative distribution F(t) can be determined from step input.
Cumulative distribution gives the fraction of material F(t) that has been in the reactor at time t or less.
Step tracer experiment
- Consider constant tracer addition to a feed that is initiated at t=0
Cin(t)={0C0,constantt<0t≥0
The concentration of tracer in feed is kept at this level until the concentration in the effluent is almost the same as the feed.
As inlet concentration is constant with time, C0, we can take it out of the integral sign:
Cout(t)=C0∫0tE(t′)dt′
- Dividing by t0:
[C0Cout(t)]step=∫0tE(t′)dt′=F(t)
Step tracer experiment
F(t)=[C0Cout(t)]step(4)
- We differentiate Equation 4 to obtain RTD function:
E(t)=dtdF=dtd[C0Cout(t)]step
Positive step is usually easier to carry out experimentally than the pulse test.
Total amount of tracer in feed over the period of test does not have to be known
Drawbacks
- It may be difficult to maintain constant tracer concentration in the feed.
- Obtaining RTD involves differentiation of the data. ( differentiation can lead to large errors. )
- A large amount of tracer is required.
Other Tracer Techniques
Negative step (elution), Frequency response method, Methods that use inputs other than pulse or step
These techniques are much more difficult to carry out and are not encountered often.
Integral relationships
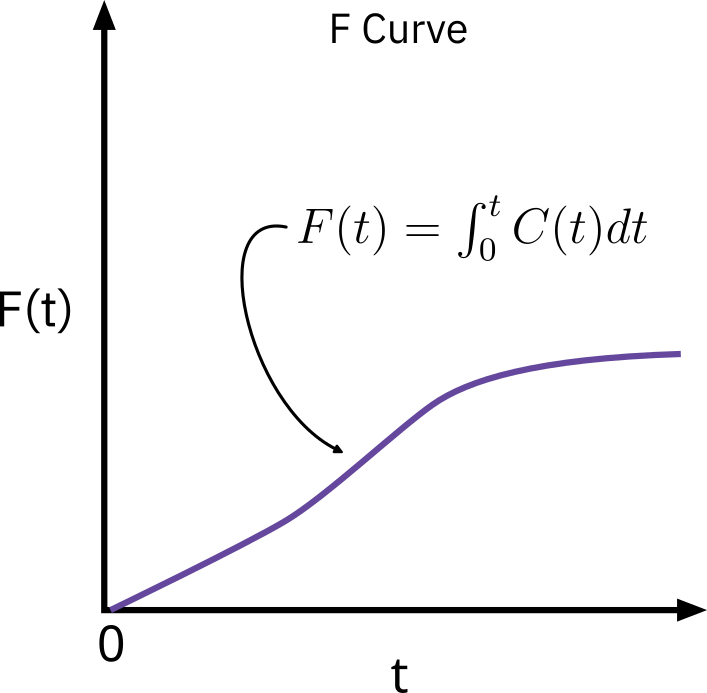
Sometimes F curve is used in the same manner as the RTD in modeling chemical reactors.
Fraction of effluent that has been in the reactor for less than t
F(t)=∫0tE(t)dt
Fraction of effluent that has been in the reactor for longer than t
1−F(t)=∫t∞E(t)dt
Mean residence time
- First moment of the RTD function
tm=∫0∞E(t)dt∫0∞tE(t)dt=∫0∞tE(t)dt
In absence of dispersion, and for constant volumetric flow rate,
tm=τ⇒V=υtm only for closed systems
Other moments of RTD
Variance (σ2): Magnitude indicates spread of distribution
σ2=∫0∞(t−tm)2E(t)dt
Skewness (s3): Magnitude measures extent that distribution is skewed in one direction in reference to mean
s3=σ3/21∫0∞(t−tm)3E(t)dt
Normalized RTD function
Frequently a normalized function is used instead of E(t).
Let θ≡τt : Number of reactor volumes of fluid based on entrance conditions that have flowed through the reactor in time t
E(θ)=τE(t);∫0∞E(θ)dθ=1
The flow performance inside reactors of different sizes can be compared directly.
If normalized function E(Θ) is used, all perfectly mixed CSTRs have numerically the same RTD. If the simple function E(t) is used, numerical values of E(t) can differ substantially.
Internal-age distribution I(α)
A function such that I(α)Δα is the fraction of material inside the reactor that has been inside for a period of time between α and α+Δα.
In catalytic reaction using catalyst whose activity decays with time, I(α) is of importance and can be used to model the reactor.
I(α)=τ(1−F(α))
E(α)=−dαd[τI(α)]
For CSTR
I(α)=−τ1e−α/τ
RTD in ideal reactors: batch and PFR
E(t)=δ(t−τ) (Dirac delta function)
δ(x)={0∞when x=0when x=0
Properties of Dirac delta function
∫−∞∞δ(x)dx=1;∫−∞∞g(x)δ(x−τ)dx=g(τ)
- Mean Residence Time
tm=∫0∞tE(t)dt=∫0∞tδ(t−τ)dt=τ
- Variance σ2=∫0∞(t−τ)2δ(t−τ)dt=0
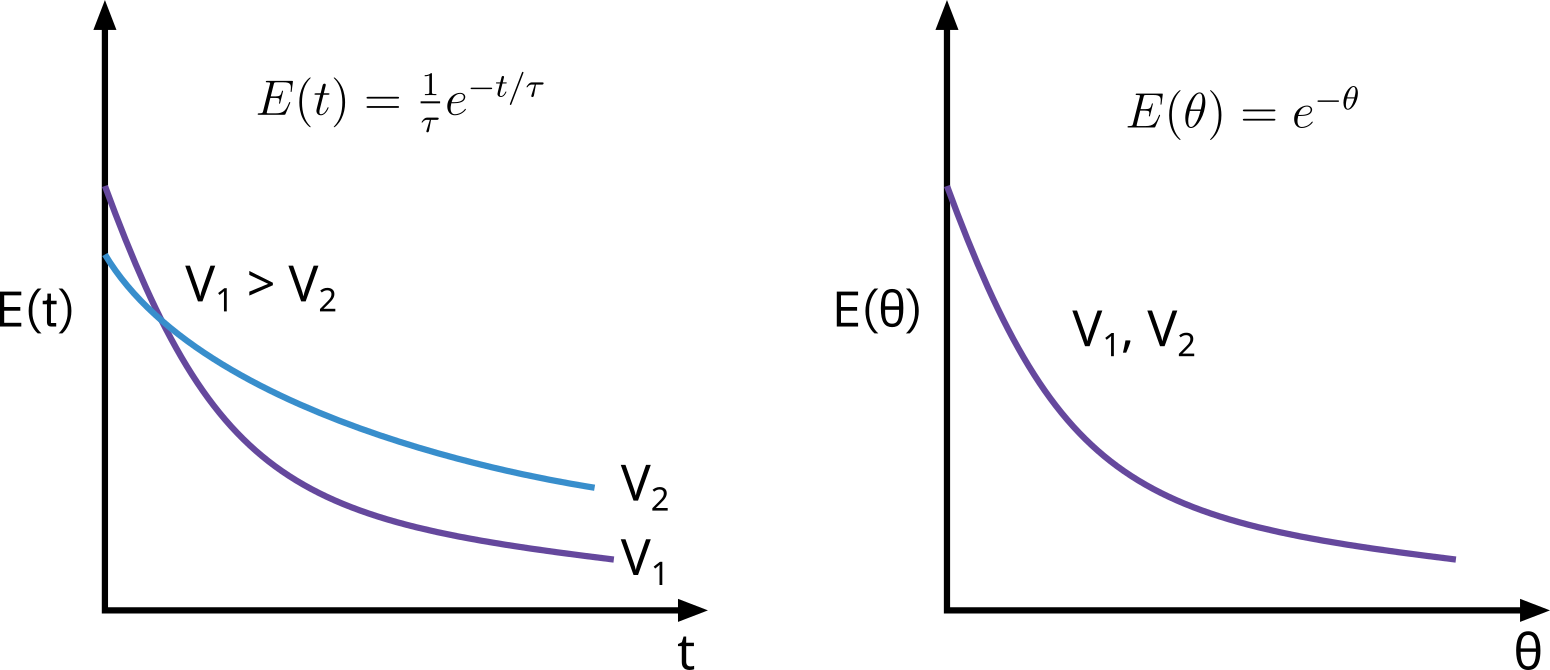
Single-CSTR RTD
Concentration in effluent stream is identical to the concentration throughout the reactor.
Material balance on an inert tracer injected as a pulse at t=0
In−Out=Accumulation⇒0−υC=VdtdC
- Initial Condition: at t=0C=C0
C(t)=C0e−t/τ
- RTD Function
E(t)=∫0∞C(t)dtC(t)=∫0∞C0e−t/τdtC0e−t/τ=τe−t/τ
Single-CSTR RTD
- Normalized RTD Function
E(θ)=e−θwhereθ=τt;E(θ)=τE(t)
Cumulative Distribution Function F(t)
F(t)=∫0tE(t)dt=∫0tτe−t/τdt
F(t)=1−e−t/τ;F(θ)=1−e−θ
Mean residence time tm=∫0∞tE(t)dt=∫0∞τte−t/τdt=τ
σ2=∫0∞τ(t−τ)2e−t/τdt=τ2∫0∞(x−1)2e−xdx=τ2
σ=τ: Standard deviation is as large as the mean
PFR/CSTR series RTD
In some stirred tanks, there is a highly agitated zone in the vicinity of the impeller → CSTR
Depending on the location of the inlet and outlet, the reacting mixture may follow a tortuous path either before entering or after leaving the perfectly mixed zone → PFR
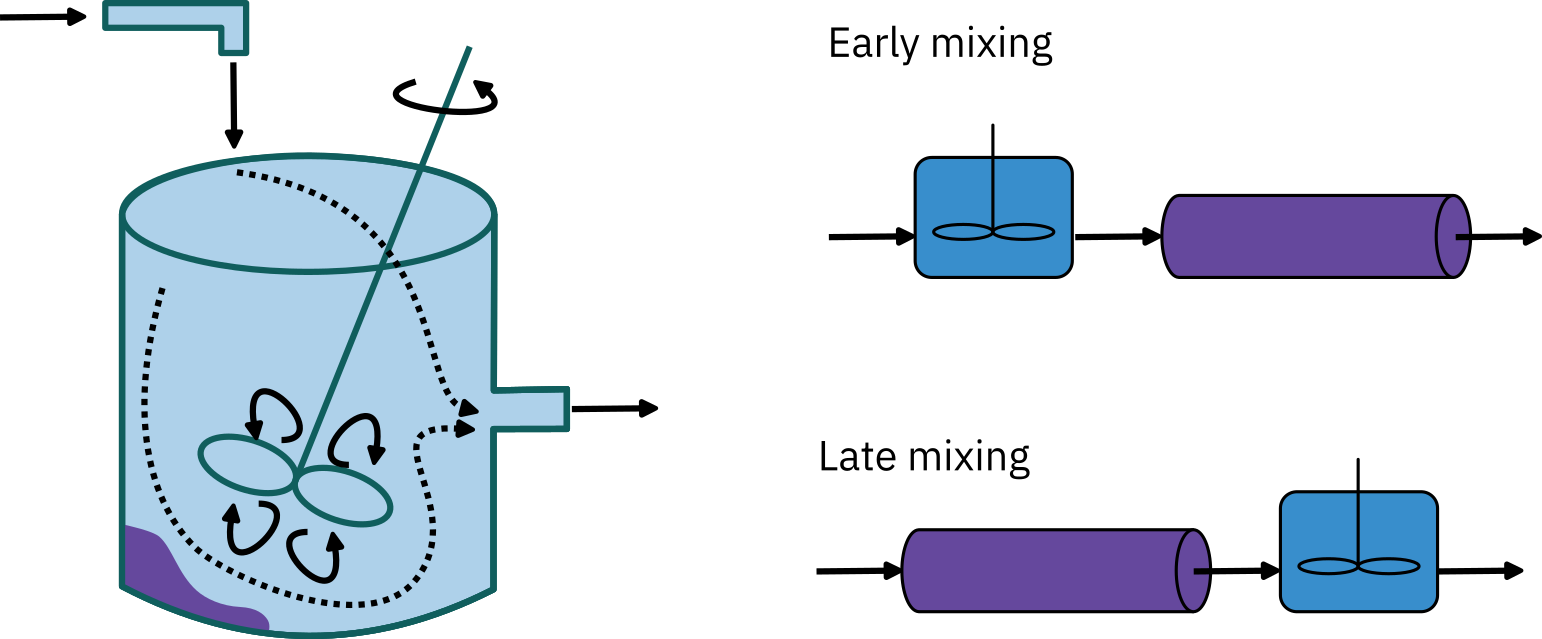
PFR/CSTR series RTD
Early mixing: C=C0e−t/τs; τs: CSTR mean RT; τp: PFR mean RT
This conc. output will be delayed by τp at the outlet plug flow section
RTD E(t)={0τse−(t−τp)/τst<τpt≥τp
Late Mixing
E(t)={0τse−(t−τp)/τst<τpt≥τp
- Exactly same as early mixing
- Even though RTD will be the same for both these cases, conversion can be very different
- RTD is not a complete description of the structure for a particular reactor / reactor systems
Diagnostics and troubleshooting
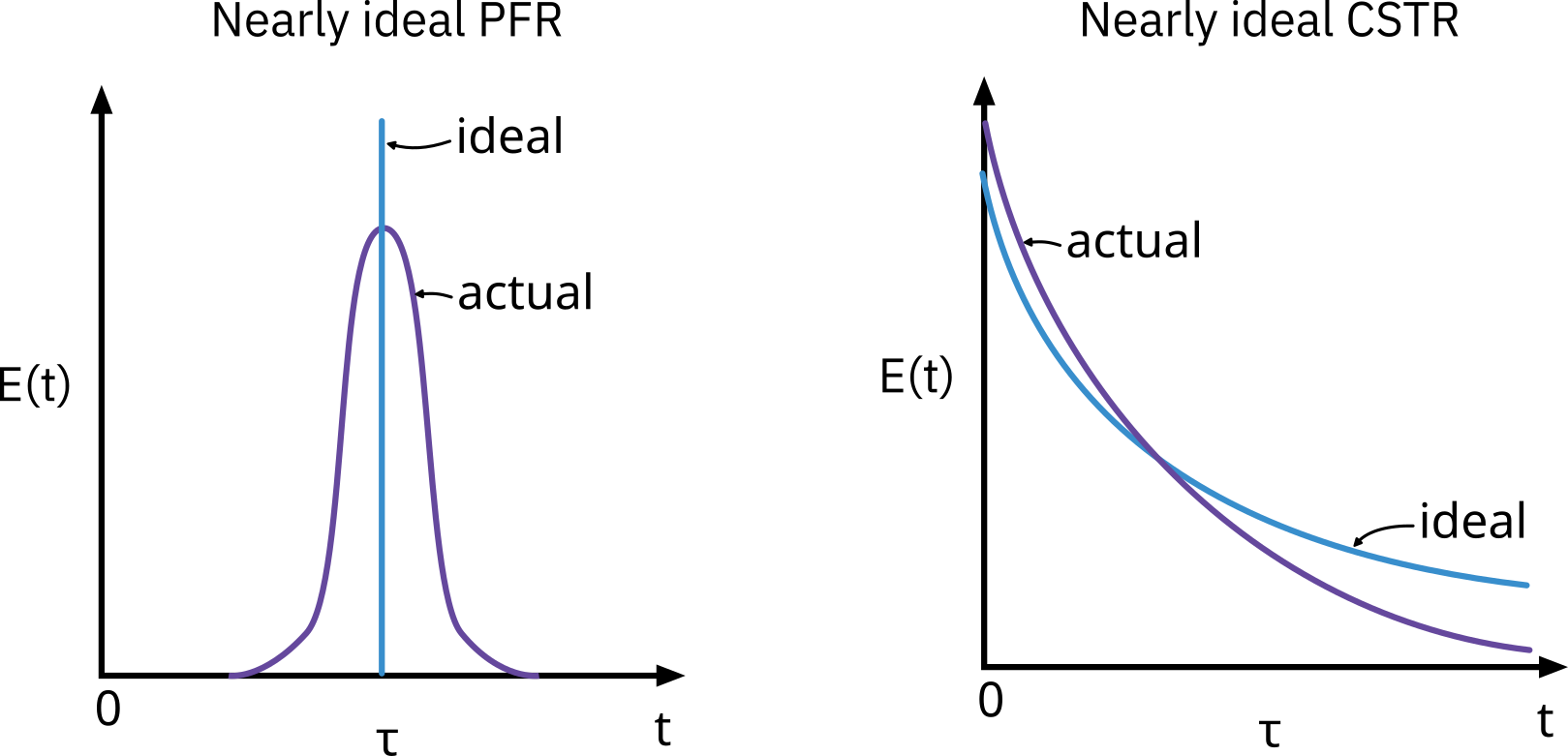
Diagnostics and troubleshooting

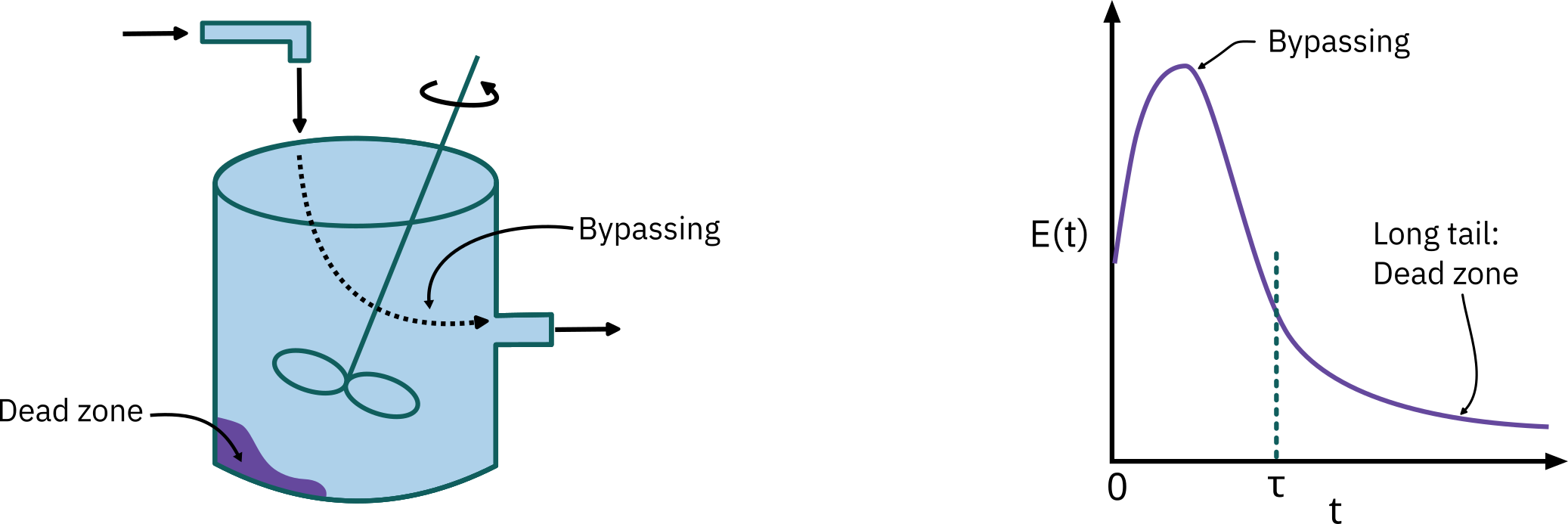
This component is an instance of the CodeMirror interactive text editor. The editor has been configured so that the Tab key controls the indentation of code. To move focus away from the editor, press the Escape key, and then press the Tab key directly after it. Escape and then Shift-Tab can also be used to move focus backwards.

Chemical Reaction Engineering
