External and internal diffusion effects
Chemical Reaction Engineering
Steps in a heterogeneous catalytic reaction
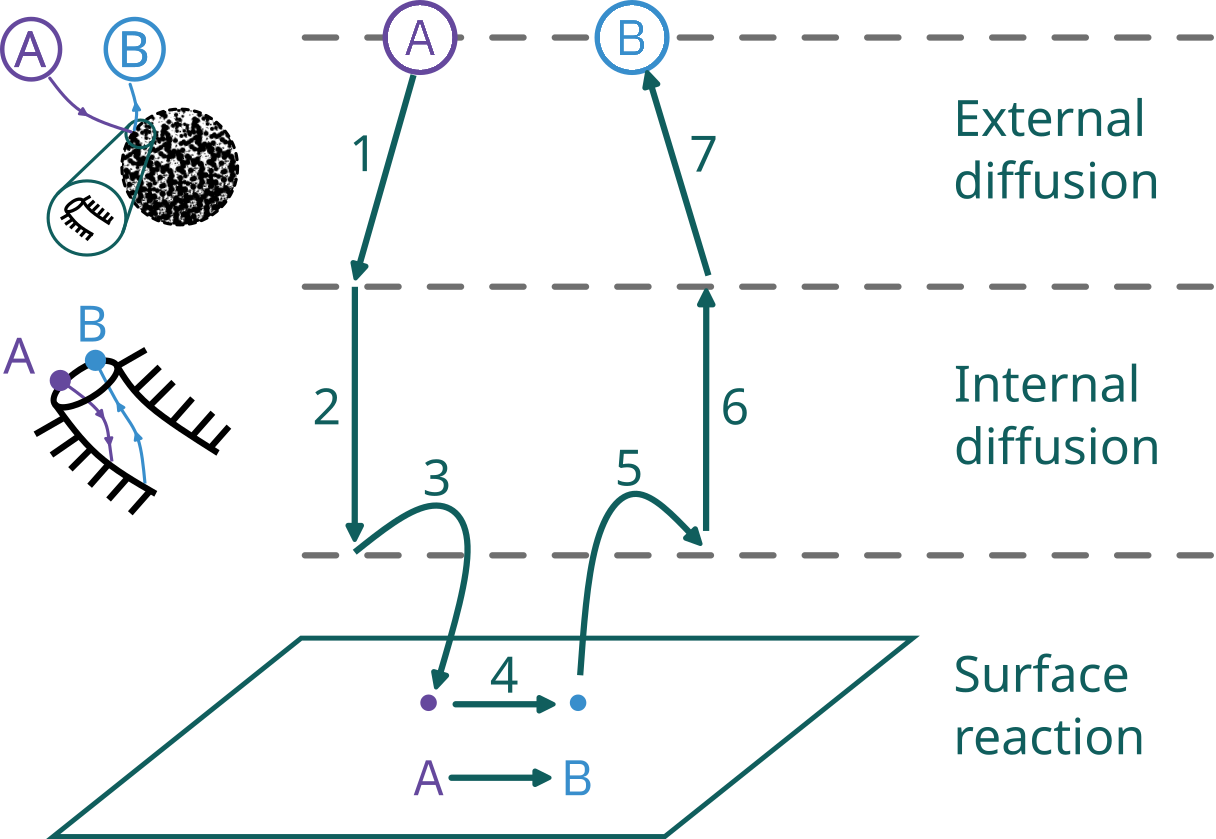
Diffusion effects
Industrial reactions at high temperature
- Limited by the rate of mass transfer between bulk fluid and the catalytic surface.
Mass transfer
- Any process in which diffusion plays a role.
- Rate laws cannot be applied directly.
- Need to consider fluid velocity and fluid properties while writing molar balances.
External mass transfer
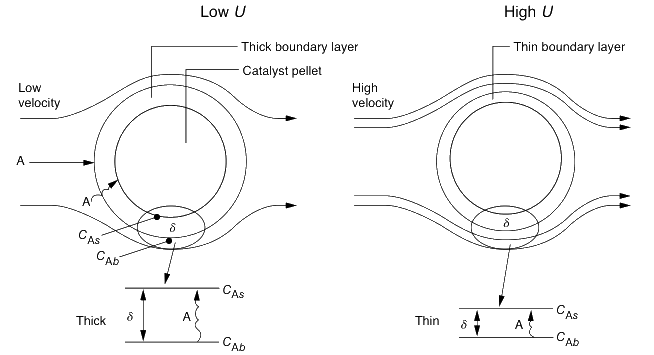
External mass transfer
Internal mass transfer
Diffusion: definitions
Molar flux with no diffusion
WAz=ACCAυ=ACFAz
m2⋅smolm3mol⋅sm3⋅m21
- FAz: Uniform at a given cross section (plug flow assumption)
Diffusion
- Spontaneous intermingling or mixing of atoms or molecules by random thermal motion.
- Gives rise to the motion of species relative to the motion of the mixture.
- From regions of high concentration to regions of low concentration in the absence of other gradients.
- Diffusion results in a molar flux of the species (A), WA (moles/area time), in the direction of the concentration gradient.
WA=iWAx+jWAy+kWAz[Rectangular coordinates]
⇒ Need to develop mole balance that incorporates both diffusion and reaction.
Mole balance in rectangular coordinates

Mole balance in rectangular coordinates
+++=[molar flow rate in]z−[molar flow rate in]y−[molar flow rate in]x−[rate of generation][rate of accumulation][molar flow rate out]z+Δz[molar flow rate out]y+Δy[molar flow rate out]x+Δx
ΔxΔyWAzz+ΔzΔyWAxx−−ΔxΔyWAzz+ΔzΔzΔyWAxx+Δx+ΔxΔzWAyy+rAΔxΔyΔz−=ΔxΔzWAyy+ΔyΔxΔyΔz∂t∂CA
Differential Form:
Dividing by ΔxΔyΔz and taking the limit as they go to zero:
∂x∂WAx+∂y∂WAy+∂z∂WAz+rA=∂t∂CA
Molar Flux
- WA: Total molar flux of species A
- JA: Molecular diffusion flux relative to bulk motion of fluid due to concentration gradient
- BA: Flux resulting from bulk motion of fluid
WA=JA+BA
- BA: =yA(∑Wi)
- ∑Wi: Total flux of all molecules
- yA: mole fraction of A
- For A→B (two-component system):
WA=JA+yA(WA+WB)=JA+CAU
Fick’s law
Describes how molar diffusive flux is related to the concentration gradient.
Fourier’s Law (thermal conduction)
q=−kt∇T;kt:thermal conductivity
∇=i∂x∂+j∂y∂+k∂z∂
For Mass Transfer: Fick’s Law
JA=−DAB∇CA
- DAB: Diffusivity of A in B (m2/s)
WA=−DAB∇CA+CAU
In One Dimension
WAz=−DABdzdCA+CAUz
Evaluating Molar Flux
A diffusing in B
WA=−DAB∇CA+yA(WA+WB)
Equimolar Counter Diffusion (EMCD)
WA=−WBWA=JA=−DAB∇CA
Species A Diffusing Through Stagnant Species B ( WB=0;WA=JA+yAWA )
- Solid boundary with adjacent stagnant fluid layer
WA=1−yAJA=−1−yADAB∇CA;WA=−DABC∇ln(1−yA)
Bulk Flow of A≫ Molecular Diffusion (plug flow model)
WA=BA=yA(WA+WB)=CAU
Evaluating Molar Flux
Small Bulk Flow JA≫BA
WA=−DAB∇CA=JA
Knudsen Diffusion
Occurs in porous catalyst where diffusing molecule collides more often with catalyst walls/pore walls than with each other.
WA=JA=−Dk∇CA
Dk: Knudsen diffusivity
Diffusion and convective transport: FAz=WAzAC
- FAz: molar flow rate of A in z direction; WAz: molar flux in z; AC: cross-sectional area normal to flow
WAz=−DAzdzdCA+CAUz
FAz=WAzAC=[−DAzdzdCA+CAUz]AC
- Similar expressions for FAy and FAx.
Mole balance in rectangular coordinates
- Substituting expressions for FAz, FAy, and FAx in mole balance
DAB[∂x2∂2CA+∂y2∂2CA+∂z2∂2CA]−ux∂x∂CA−uy∂y∂CA−uz∂z∂CA+rA=∂t∂CA
- In one dimension:
DAB∂z2∂2CA−Uz∂z∂CA+rA=∂t∂CA
Boundary conditions
Concentration at boundary: @z=0→CA=CA0;@z=L→dzdCA=0
Specify flux at the boundary
No mass transfer WA=0
Molar flux at surface = rate of reaction at surface
WA∣surface=−r′′∣surface
Molar flux to boundary = convective transport across boundary layer
WA∣boundary=kc(CAb−CAs)
Temperature and pressure dependence of DAB
| Phase | cm2/s | m2/s | Temperature and pressure dependences |
|---|---|---|---|
| Gas | |||
| - Bulk | 10−1 | 10−5 | DAB(T2,P2)=DAB(T1,P1)P2P1(T1T2)1.75 |
| - Knudsen | 10−2 | 10−6 | DAB(T2)=DA(T1)(T1T2)1/2 |
| Liquid | 10−5 | 10−9 | DAB(T2)=DAB(T1)μ2μ1(T1T2) |
| Solid | 10−9 | 10−13 | DAB(T2)=DAB(T1)exp[RED(T1T2T2−T1)] |
- μ1,μ2 are the liquid viscosities at temperatures T1 and T2 respectively.
- ED is the diffusion activation energy.
- Knudsen, liquid, and solid DAB are independent of P.
Modeling diffusion with chemical reaction
- Diffusion of species through stagnant film in which no reaction takes place
- A reacts instantaneously upon reaching the surface CAs≈0
- Rate of diffusion through stagnant film = rate of reaction on the surface
Steps:
- Perform differential mole balance → Equation for WAz
- Replace WAz by appropriate expression for concentration gradient
- State boundary conditions
- Solve for concentration profile
- Solve for molar flux
Diffusion through a stagnant film

Flow Past a Single Catalytic Pellet
- Reaction takes place only on external catalyst surface and not in fluid surrounding it.
Hydrodynamic Boundary Layer: Distance from solid object to where the fluid velocity is 99% of the bulk velocity U0.
Mass Transfer Boundary Layer: Distance at which concentration of diffusing species is 99% of the bulk concentration.
- We cannot measure δ.
Diffusion through a stagnant film
- Assumption:
- Fluid layer next to solid as stagnant film (hypothetical) of thickness δ.
- All the resistance to mass transfer is within the film.
- Properties at the outer edge of the film are identical to those of bulk fluid.
- For film thickness ≪ radius of pellet:
- Curvature effects can be neglected
- Problem reduces to 1D diffusion.
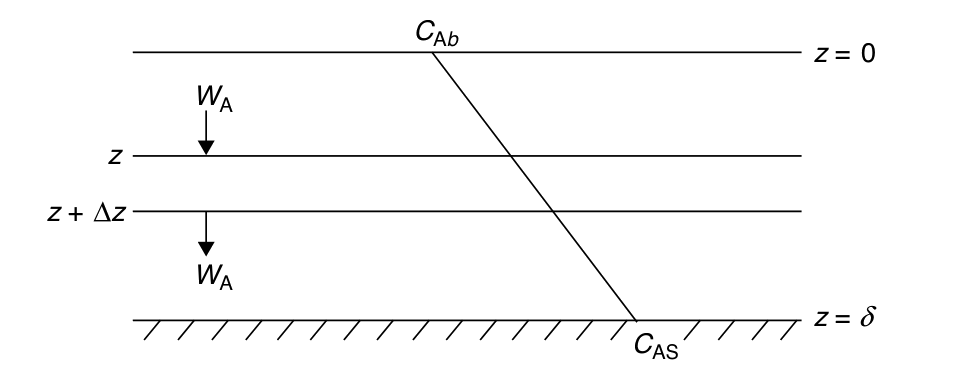
InWAzz−−OutWAzz+Δz++Generation0==Accumulation0
Diffusion through a stagnant film
Dividing by Δz and taking the limit as Δz→0 dzdWAz=0
For diffusion through stagnant film at dilute concentrations,
JA≫yA(WA+WB)
WAz=−DABdzdCA(also for EMCD)
- Therefore, mole balance becomes
dz2d2CA=0
- Boundary Conditions (BCs)
- At z=0, CA=CAs; At z=δ, CA=CAb
Diffusion through a stagnant film
Integrating twice CA=k1z+k2⟹CAs=k2and(δCAb−CAs)=k1
Substituting BCs
CA=CAs+(CAb−CAs)δz
- Surface Flux
WAzδ=−DABdzdCAδ
WAz=δDAB[CAb−CAs]
- At steady state: Flux of A to the surface=Rate of reaction of A on surface
The mass transfer coefficient
kc=δDAB
- Average molar flux from the bulk fluid to the surface
WAz=kc(CAb−CAs)
WAz=Flux=ResistanceDriving force=(kc1)CAb−CAs
The mass transfer coefficient is found by experimentation
Correlations analogous to what one finds for a heat transfer coefficient.
Sh=2+0.6Re1/2Sc1/3 Fro¨ssling correlation
Sh=DABkcL;Sc=DABν=ρDABμ;Re=νUL=μULρ
Mass transfer–limited reactions in packed beds
[Molar rate in]−[Molar rate out]+[Molar rate of generation]=[Molar rate of accumulation]
- In one dimension at steady state
FAzz−FAzz+Δz+rA′′c(AcΔz)=0
- Dividing by AcΔz and taking the limit as Δz→0
−Ac1(dzdFAz)+rA′′c=0
Mass transfer–limited reactions in packed beds
- Express FAz and r′′ in terms of concentration
FAz=AcWAz=(JAz+BAz)Ac
In almost all situations involving flow in packed-bed reactors, the amount of material transported by diffusion or dispersion in the axial direction is negligible compared with that transported by convection (i.e., bulk flow)
Neglecting dispersion as JAz≪BAz
FAz=AcWAz=AcBAz=UcAc
−dzd(CU)+rA′′c=0
For constant superficial velocity
−UdzdC+rA′′c=0
Mass transfer–limited reactions in packed beds
The boundary condition at the external surface is
−rA′′=WAr=kc(CA−CAs)
−UdzdC−kcac(CA−CAs)=0
−UdzdC=kcac(CA−CAs)
In most mass transfer-limited reactions, the surface concentration is negligible with respect to the bulk concentration (CA≫CAs)
−UdzdC=kcacCA
At z=0,CA=CA0
CA0CA=exp(−Ukcacz);ln1−X1=UkcacL
Diffusion and reactions in homogeneous systems
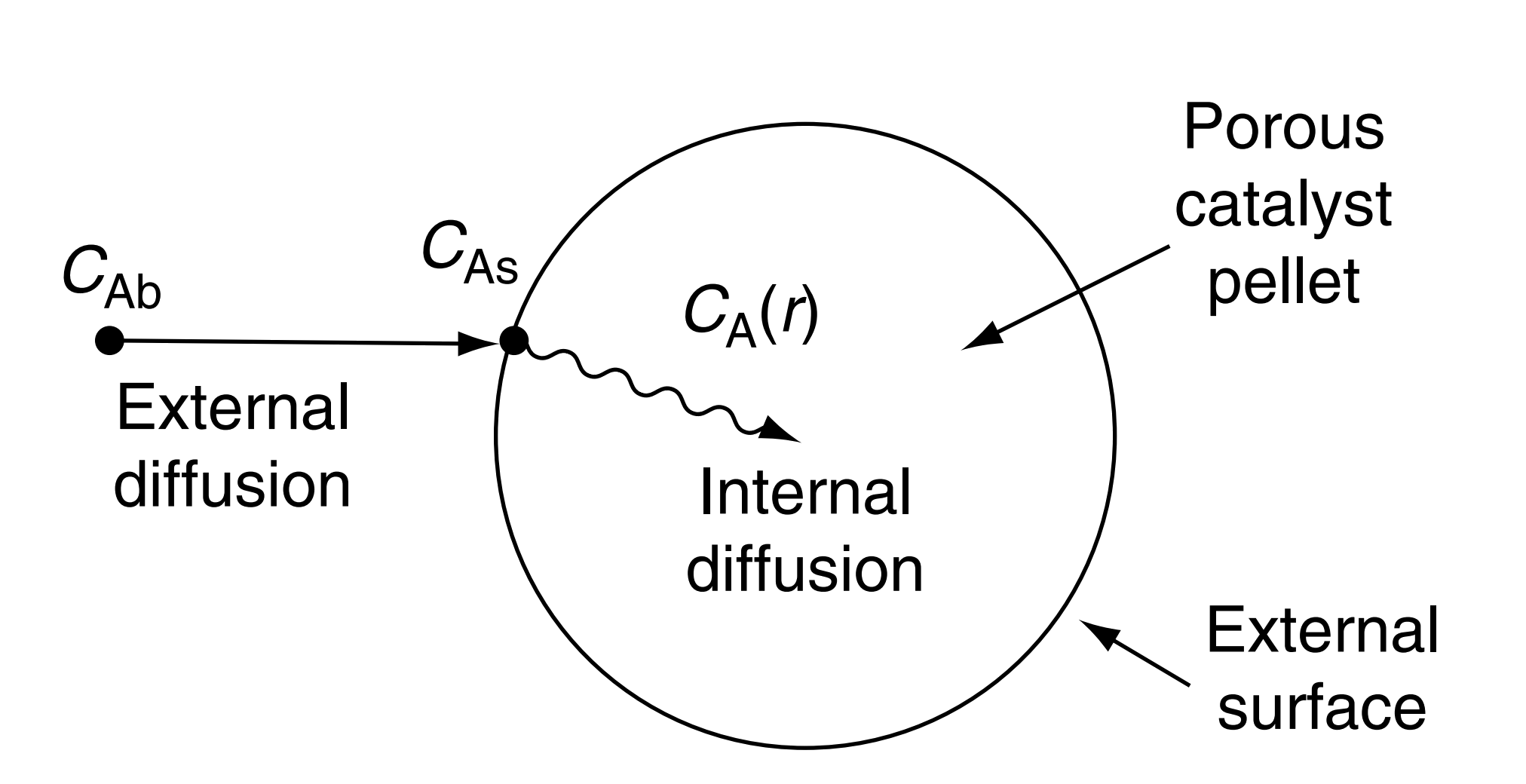
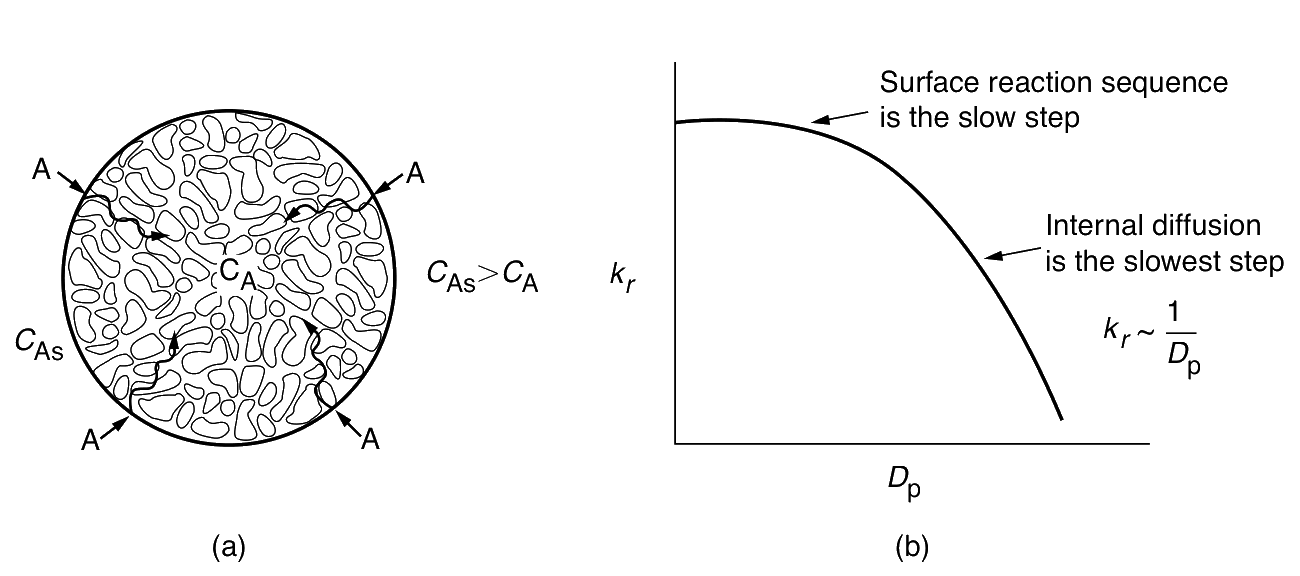
- When reactants must diffuse inside a catalyst pellet in order to react
- The concentration at the pore mouth must be higher than that inside the pore.
- Entire catalyst surface is not accessible to the same concentration
- The rate of reaction to vary throughout the pellet.
Diffusion and Reaction in Homogeneous Systems
- Mole balance on species A for 1D diffusion at steady state
−dzdWAz+rA=0
WAz=−DABdzdCA
DABdz2d2CA+rA=0
Applications
- Medicine
- Cancer treatment using drug-laced particulates
- Tissue engineering
Effective diffusivity
De=τ~DABϕpσc;WAz=−DedzdCA
The effective diffusivity accounts for the fact that:
- Not all of the area normal to the direction of the flux is available (i.e., the area occupied by solids) for the molecules to diffuse, (porosity, ϕp)
- The paths are tortuous (tortuosity, τ~)
- The pores are of varying cross-sectional areas (Constriction factor, σc)
Diffusion and reactions in spherical catalyst pellets

Consider irreversible isomerization reaction AB
The reaction occurs on the surface of pore walls within a spherical pellet of radius R.
Assumptions
- Steady state; spherical coordinates
- Constant pressure and temperature conditions
- Steady state mole balance on a spherical shell r→r+Δr
(In at r)(WAr4πr2∣r)−−(Out at r+Δr)(WAr4πr2∣r+Δr)++(Generation within Δr)(rA′ρc4πrm2Δr)==00
- Dividing by −4πΔr and taking limit as Δr→0
drd(WArr2)−rA′ρcr2=0
Diffusion and reactions in spherical catalyst pellets
WAr=−DedrdCA
dr−De(dCA/dr)r2−r2ρcrA′=0
Reaction rate {rA′=knCAn}
- per unit surface area −rA′′
- per unit mass of catalyst −rA′=Sa(−rA′′)
- per unit volume −rA=ρc(−rA′)=ρcSa(−rA′′)
dr2d2CA+r2(drdCA)−DeknCAn=0
Boundary conditions
- At the center of pellet: at r=0, CA is finite
- At the external surface: at r=R, CA=CAs
Diffusion and reactions in spherical catalyst pellets
Dimensionless form
ψ=CAsCA;λ=Rr
Boundary conditions
- At λ=0, ψ is finite
- At λ=1, ψ=1
dλ2d2ψ+λ2(dλdψ)−ϕ2ψn=0
- Thiele modulus
ϕn2=DeknR2CAsn−1=De(RCAs−0)knRCAsn=“a” diffusion rate“a” surface reaction rate
- When the Thiele modulus is large, internal diffusion usually limits the overall rate of reaction; when ϕn is small, the surface reaction is usually rate-limiting.
Diffusion and reactions in spherical catalyst pellets
- Dimensionless concentration profile
ψ=CAsCA=λ1(sinhϕ1sinhϕ1λ)
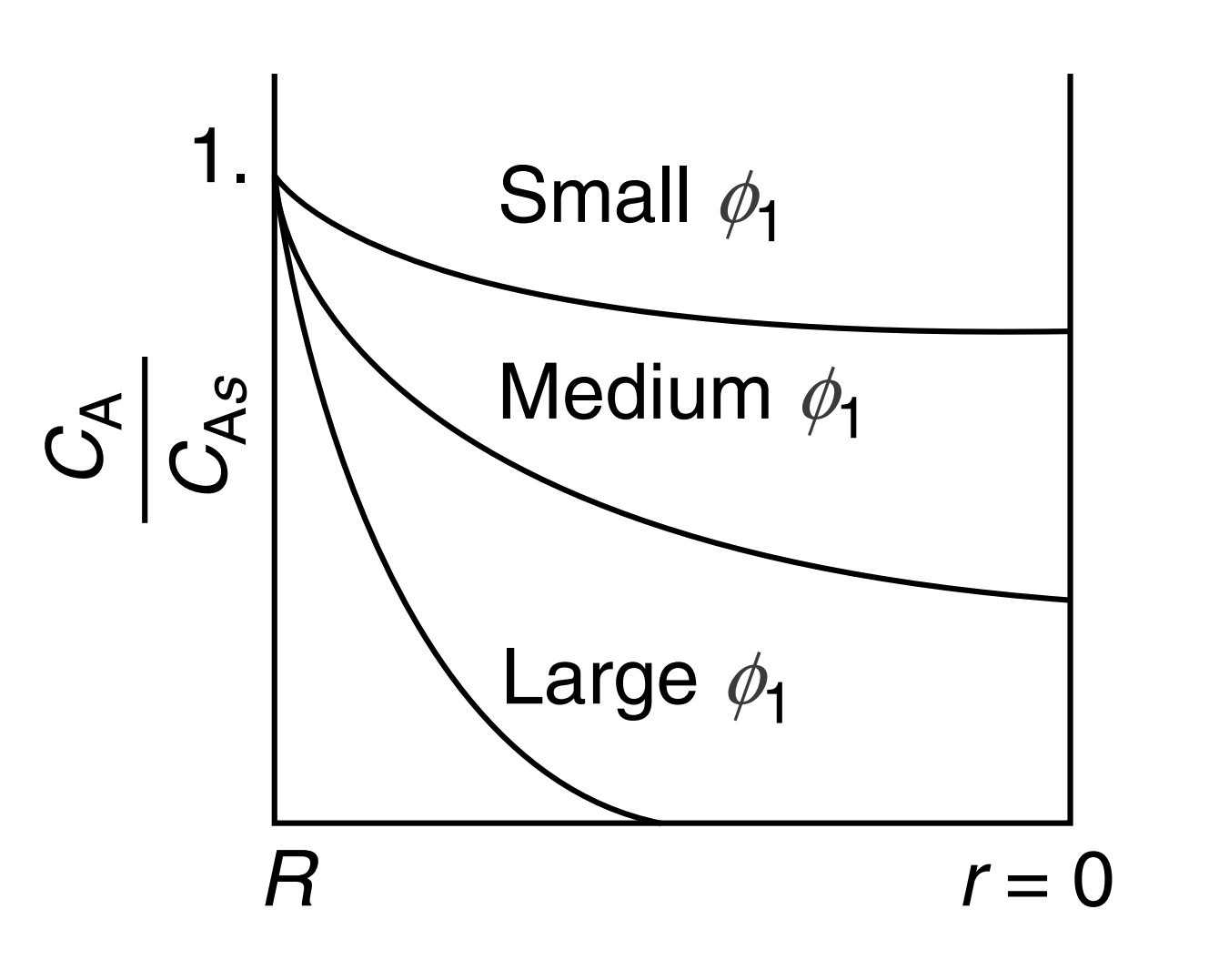
The internal effectiveness factor
- The magnitude of the effectiveness factor (ranging from 0 to 1) indicates the relative importance of diffusion and reaction limitations.
η=Rate of reaction that would result if entireinterior surface were exposed to the externalpellet surface conditions CAs,TsActual overall rate of reaction
- Overall (observed) rate
η=−rAs−rA=−rAs′−rA′=−rAs′′−rA′′
- Effectiveness factor for first order reaction spherical pellet
η=ϕ123(ϕ1cothϕ1−1)
- Reaction rate −rA=η(k1CAs)
If ϕ1<2: η≈ϕ123[ϕ1−1]
If ϕ1>20: η≈ϕ123
The internal effectiveness factor

The internal effectiveness factor

Determination of limiting situations from reaction- rate data
Reaction rate per unit mass of catalyst −rA′=kcacCA
kc∝dp1/2U1/2;ac∝dp1
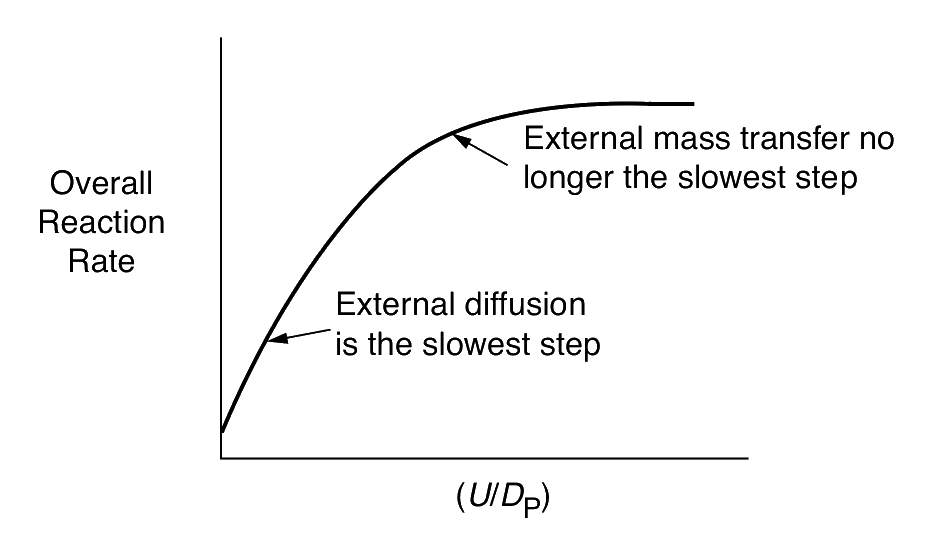
For external mass transfer–limited reaction
−rA′∝dp3/2U1/2
| Type of Limitation | Velocity | Particle Size | Temperature |
|---|---|---|---|
| External diffusion | U1/2 | (dp)−3/2 | ≈ Linear |
| Internal diffusion | Independent | (dp)−1 | Exponential |
| Surface reaction | Independent | Independent | Exponential |
This component is an instance of the CodeMirror interactive text editor. The editor has been configured so that the Tab key controls the indentation of code. To move focus away from the editor, press the Escape key, and then press the Tab key directly after it. Escape and then Shift-Tab can also be used to move focus backwards.

Chemical Reaction Engineering