CRE | Chemical Reaction Engineering – Reaction mechanisms and catalysis

Nonelementary rate laws

Rate law is typically determined from experimental data
Elementary reaction kinetics: the reaction orders and stoichiometric coefficients are identical
Nonelementary reaction kinetics: no direct correspondence between reaction order and stoichiometry

$\ce{CH3CHO -> CH4 + CO}; \qquad -r_{\ce{CH3CHO}} = k C_{\ce{CH3CHO}}^{3/2}$

$\ce{H2 + Br2 -> 2 HBr}; \qquad -r_{\ce{HBr}} = \frac{ k_1 C_{\ce{H2}} C_{\ce{Br2}}^{3/2} } { C_{\ce{H2}} + k_2 C_{\ce{Br2}} }$
Why the rate laws are complicated? $\rightarrow$ Reaction mechanism
Use the experimental rate law to postulate a reaction mechanism

In practice, knowledge of the reaction mechanism helps use to design better catalyst, troubleshoot, aid in troubleshooting poor reactor performance

Nonelementary rate laws

Nonelementary kinetics are the result of multiple elementary reaction steps
One or more active intermediates are involved

Active Intermediate

A high energy species that reacts further very fast. It is consumed as fast as it is formed
It can be
- A high energy molecule
- A free radical
- An ionic Intermediate
It is present at extremely low concentration.

Pseudo-Steady-State Hypothesis (PSSH)

Net rate of formation of reactive intermediate $\approx$ 0
If the active intermediate appears in n reactions, then

$r_{A^*} = \sum_{i = 1}^{n} r_{i, A^*} = 0$

How do we determine the mechanism?

Postulate a reaction mechanism that is a series of elementary reactions
Derive a rate equation for the postulated mechanism
Is the rate equation for the postulated mechanism consistent with the experimental results?

Searching for a mechanism

Propose an active intermediate(s).
Propose a mechanism, utilizing the rate law obtained from experimental data, if possible.
Model each reaction in the mechanism sequence as an elementary reaction.
After writing rate laws for the rate of formation of desired product, write the rate laws for each of the active intermediates.
Write the net rate of formation for the active intermediate and use the PSSH.
Eliminate the concentrations of the intermediate species in the rate laws by solving the simultaneous equations developed in Steps 4 and 5.
If the derived rate law does not agree with experimental observation, assume a new mechanism and/or intermediates and go to Step 3. A strong background in organic and inorganic chemistry is helpful in predicting the activated intermediates for the reaction under consideration.

Rules of thumb for development of a mechanism

Species having the concentration(s) appearing in the denominator of the rate law probably collide with the active intermediate

$\ce{M + A* -> [Collision products]} \qquad -r_{A1}^* = k_1 C_M C_{A \cdot}$
If a constant appears in the denominator, one of the reaction steps is probably the spontaneous decomposition of the active intermediate

$\ce{A* -> [Decomposition products]} \qquad -r_{A2}^* = k_2 C_{A \cdot}$
Species having the concentration(s) appearing in the numerator of the rate law probably produce the active intermediate in one of the reaction steps

$\ce{[Reactants] -> A* + [Other products]} \qquad r_{A3}^* = k_3 C_{Reactants}$

PSSH explanation for common first-order reactions

PSSH theory helps to explain why many reactions, such as the decomposition of dimethyl ether commonly exhibit first-order kinetics

$\ce{(CH3)2O -> CH4 + H2 + CO}$
$\ce{ A -> Products }; \qquad -r_A = k C_A$

The reaction is first order but not elementary.
Mechanism
- Activation:k $\ce{A + M ->[k_1] A^* + M}; \qquad r_{1,\ce{A^*}} = k_1 C_A C_M$
- Deactivation: $\ce{A^* + M ->[k_2] A + M}; \qquad r_{2,\ce{A^*}} = k_2 C_{\ce{A^*}} C_M$
- Decomposition: $\ce{A^* ->[k_3] P}; \qquad r_{3,\ce{A^*}} = k_3 C_{\ce{A^*}}$
Rate of formation of product

$r_p = k_3 C_{\ce{A^*}}$

Need to eliminate $C_{\ce{A^*}}$

PSSH explanation for common first-order reactions

PSSH: $r_{A^*} = 0$

$\begin{aligned} r_{A^*} &= k_1 C_A C_M - k_2 C_{A^*} C_M - k_3 C_{A^*} = 0 \\ \\ k_1 C_A C_M &= C_{A^*} (k_2 C_M + k_3) \\ \\ C_{A^*} &= \frac{k_1 C_A C_M}{k_2 C_M + k_3} \\ \\ r_P &= \frac{k_3 k_1 C_A C_M}{k_2 C_M + k_3} \end{aligned}$
$C_M$ is constant

$k = \frac{k_3 k_1 C_M}{k_2 C_M + k_3}$

and

$-r_A = k C_A$

Catalysts & catalysis

Definition
- Fogler: A substance that affects the rate of a reaction but emerges from the process unchanged.
- Ostwald (1895): A catalyst accelerates a chemical reaction without affecting the position of the equilibrium.
Positive catalyst increases reaction rate.
Negative catalyst decreases reaction rate.
About 75% of all chemicals are produced by catalytic process.
Catalyst can be:
- Gas ( $\ce{NO_x}$ ): Nitric Oxide (NO) for the Ostwald Process: In the industrial synthesis of nitric acid, nitric oxide acts as a catalyst in the oxidation of ammonia to nitrogen dioxide. This is part of a gas-phase reaction system where NO is regenerated and acts catalytically.
- Liquid ( $\ce{H2SO4}$ ): Sulfuric Acid in Alkylation: Used in the oil refining industry, sulfuric acid serves as a liquid phase catalyst in alkylation reactions where isobutane is alkylated with olefins to produce higher molecular weight isoparaffins. The reaction occurs in the liquid phase, with sulfuric acid enhancing the reaction by protonating the olefin to form a more reactive carbocation intermediate.
- Solid ( $\ce{Ag}$ ): Silver on Alumina for Ethylene Oxide Production: Silver deposited on an alumina support is a crucial catalyst for the oxidation of ethylene to ethylene oxide, a precursor in the production of ethylene glycol. This is an example of a solid catalyst used in a gas-phase reaction, highlighting the versatility of catalyst forms and applications.

In this lecture only solid catalysts will be considered.

Heterogeneous catalysis at different scales

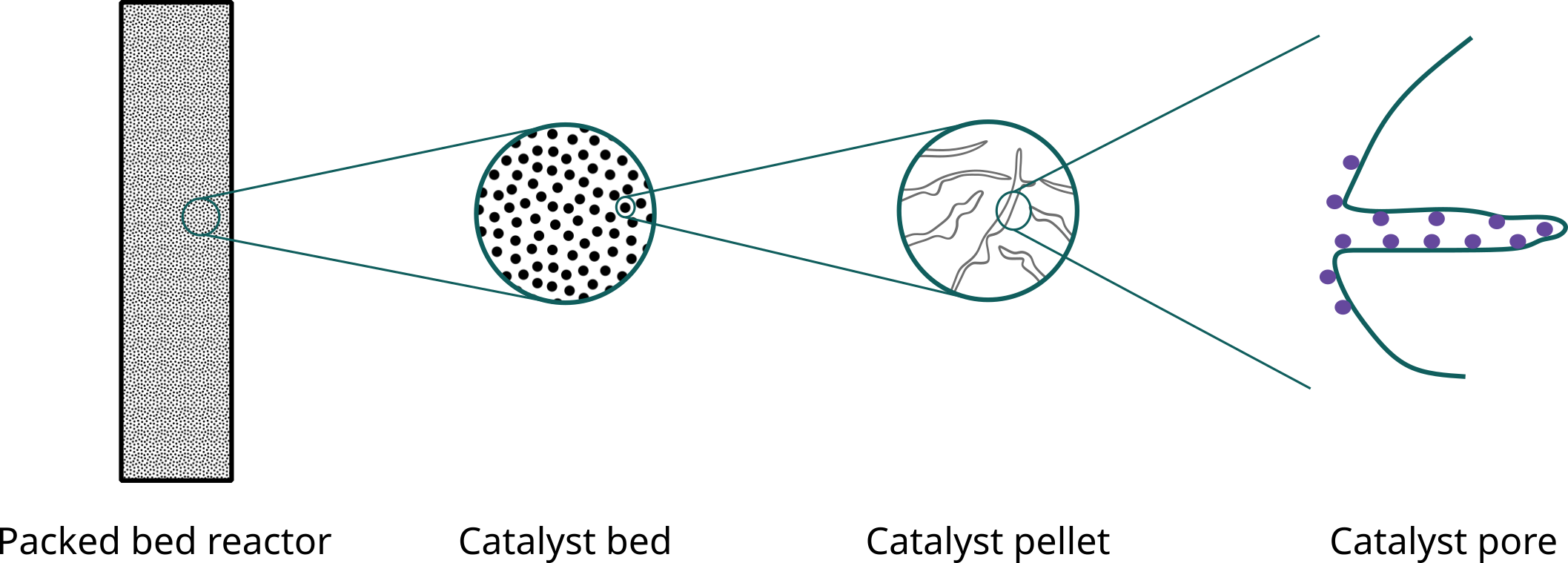
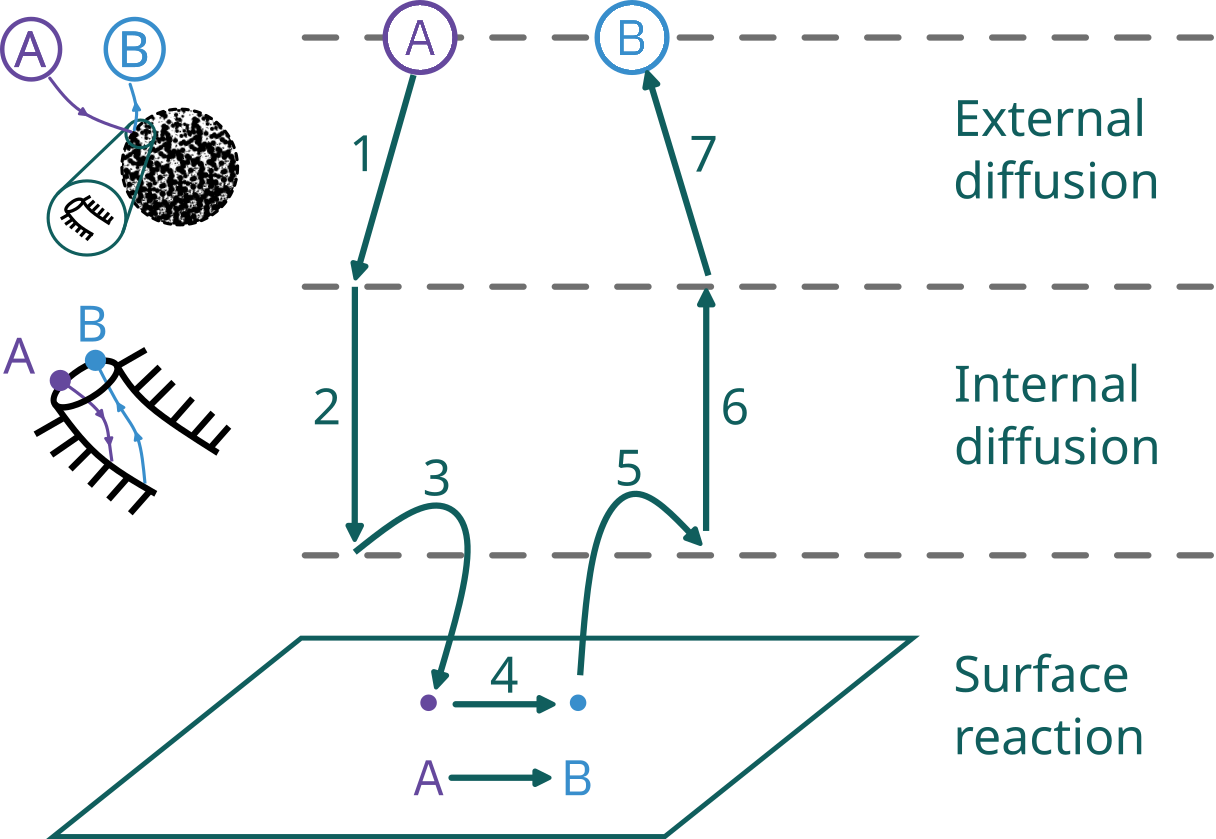
Steps in a heterogeneous catalytic reaction

Adsorption step

Chemisorption is a necessary part of catalytic processes
Adsorption data are often presented using adsorption isotherms, which show how much gas is adsorbed by a solid at various pressures at a constant temperature.
We first propose an adsorption mechanism and derive an isotherm from it. This theoretical isotherm is then compared with experimental data.
If the theoretical isotherm aligns well with the experimental data, it suggests that the model accurately reflects the physical processes occurring within the system. Discrepancies between the predicted and actual data indicate that the model may not capture one or more crucial aspects of the physical system.

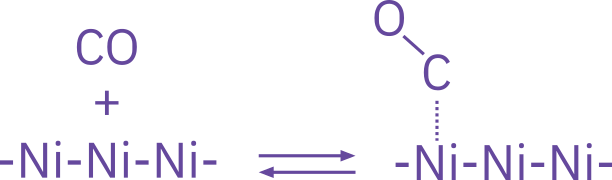
Molecular adsorption

$\ce{CO + S <=> CO*S}$

Dissociative adsorption

$\ce{CO + 2S <=> C*S + O*S}$

Langmuir isotherm: molecular adsorption

The adsorption of A (gas phase) on an active site S is represented by:

$\ce{A(g) + S <=> A*S }$

S is a vacant surface site. $\ce{A*S}$ is A bound to a surface site.
Rate of adsorption = rate of attachment - rate of detachment

$r_{AD} = k_A P_A C_v - k_{-A} C_{\ce{A*S}}$
- The rate is directly proportional to the number of collisions between the reactant molecules and the catalyst surface, which is influenced by the partial pressure of the reactant ( $P_A$ ).
- Additionally, the reaction rate is dependent on the availability of vacant active sites on the catalyst surface.
Adsorption equilibrium constant $K_A = k_A/k_{-A}$

$r_{\text{AD}} = k_A P_A C_v - k_{-A} C_{\ce{A*S}} \qquad r_{\text{AD}} = k_A \left( P_A C_v - \frac{k_{-A}}{k_A} C_{\ce{A*S}} \right)$

$\Rightarrow r_{\text{AD}} = k_A \left( P_A C_v - \frac{C_{\ce{A*S}}}{K_A} \right)$

Site balance

$C_t$ : Total number of active sites per unit mass of catalyst divided by Avogadro’s number (mol/g cat)
$C_v$ : Number of vacant sites per unit mass of catalyst divided by Avogadro’s number
$C_v$ is not measurable, but the total number of sites $C_t$ can be measured
Site balance

In the absence of catalyst deactivation, assume the total number of active sites remains constant:

$C_t = C_v + C_{\ce{A*S}} + C_{\ce{B*S}}$
We will use the site balance equation to put $C_v$ in terms of measurable species

Langmuir isotherm: molecular adsorption

Site balance

$C_t = C_v + C_{\ce{A*S}}$
At equilibrium: The net rate of adsorption is zero. Setting $r_{AD}=0$ we can obtain equation for concentration of A adsorbed on the surface

$C_{\ce{A*S}} = K_A C_v P_A \qquad C_{\ce{A*S}} = K_A P_A (C_t - C_{\ce{A*S}})$
Langmuir isotherm: By rearranging, we obtain the Langmuir isotherm

$C_{\ce{A*S}} = \frac{K_A P_A C_t} {1 + K_A P_A}$

This equation relates the equilibrium concentration of A adsorbed on the surface, $C_{\ce{A*S}}$ , as a function of the partial pressure of A
Linearized form

$\frac{P_A}{C_{\ce{A*S}}} = \frac{1}{K_A C_t} + \frac{P_A}{C_t}$

Langmuir isotherm: Dissociative adsorption

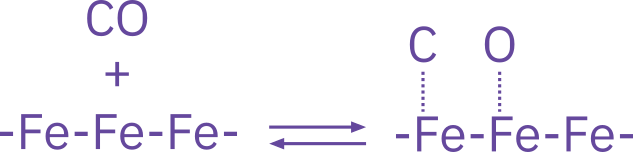
Consider the adsorption of CO on iron where CO dissociates into separate atoms

$\ce{CO + 2S <=> C*S + O*S}$

Dissociative adsorption requires two adjacent vacant sites, unlike molecular adsorption that needs only one.
The likelihood of finding two adjacent vacant sites is proportional to the square of the concentration of vacant sites, in line with the law of mass action.
Consequently, the rate of adsorption is proportional to the product of the carbon monoxide partial pressure and the square of the vacant-site concentration.
For desorption, two adjacent occupied sites are needed, making the rate of desorption proportional to the product of the occupied-site concentrations $C_\ce{C*S}$ and $C_{\ce{O*S}}$ .
The net rate of adsorption

$r_{AD} = k_A P_{\ce{CO}} C_v^2 - k_{-A} C_{\ce{C*S}} C_{\ce{O*S}}$

$r_{AD} = k_A \left( P_{\ce{CO}} C_v^2 - \frac{ C_{\ce{C*S}} C_{\ce{O*S}} } { K_A }\right) \qquad K_A = \frac{k_A}{k_{-A}}$

Langmuir isotherm: Dissociative adsorption

At equilibrium $r_{AD} = 0 \qquad \Rightarrow \qquad k_A P_{\ce{CO}} C_v^2 = k_{-A} C_{\ce{C*S}} C_{\ce{O*S}}$
For $C_{\ce{C*S}} = C_{\ce{O*S}}: \qquad (K_A P_{\ce{CO}})^{1/2} C_v = C_{\ce{O*S}}$
Substituting for $C_{\ce{C*S}}$ , and $C_{\ce{O*S}}$ in site balance equation

$C_t = C_v + C_{\ce{C*S}} + C_{\ce{O*S}}$

$C_t = C_v + (K_A P_{\ce{CO}})^{1/2} C_v + (K_A P_{\ce{CO}})^{1/2} C_v = C_v (1 + 2(K_A P_{\ce{CO}})^{1/2})$
Solving for $C_v$ $C_v = \frac{C_t}{1 + 2(K_A P_{\ce{CO}})^{1/2}}$
Langmuir isotherm:

$C_{\ce{O*S}} = \frac{(K_A P_{\ce{CO}})^{1/2} C_t}{1 + 2(K_A P_{\ce{CO}})^{1/2}} \qquad; \qquad \frac{(P_{\ce{CO}})^{1/2}} {C_{\ce{O*S}}} = \frac{1}{C_t (K_A)^{1/2}} + \frac{2 (P_{\ce{CO}})^{1/2}}{C_t}$

Langmuir isotherm adsorption

Surface reaction step: single site

After a reactant has been adsorbed onto the surface, $\ce{A*S}$ , is capable of reacting in a number of ways to form the reaction product
Single site mechanism
- The surface reaction may be a single-site mechanism in which only the site on which the reactant is adsorbed is involved in the reaction.
- An adsorbed molecule of A may isomerize (or perhaps decompose) directly on the site to which it is attached, for example, such as pentene isomerization

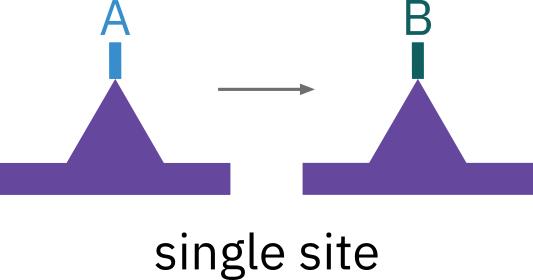
$\ce{A*S <=> B*S}$

Surface reaction rate law

$r_S = k_S C_{\ce{A*S}} - k_{-S} C_{\ce{B*S}}$

$r_S = k_S \left( C_{\ce{A*S}} -\frac{C_{\ce{B*S}}}{K_S}\right)$

$K_S = k_S/k_{-S}$

Surface reaction step: dual site

Mechanism 1

$\ce{A*S + S <=> B*S + S}$

$r_S = k_S \left( C_{\ce{A*S}} C_v -\frac{C_{\ce{B*S}} C_v}{K_S}\right)$

Mechanism 2

$\ce{A*S + B*S <=> C*S + D*S}$

$r_S = k_S \left( C_{\ce{A*S}} C_{\ce{B*S}} -\frac{C_{\ce{C*S}} C_{\ce{D*S}}}{K_S}\right)$

Mechanism 3: Two different kind of sites are involved

$\ce{A*S + B*S' <=> C*S' + D*S}$

$r_S = k_S \left( C_{\ce{A*S}} C_{\ce{B*S'}} -\frac{C_{\ce{C*S'}} C_{\ce{D*S}}}{K_S}\right)$

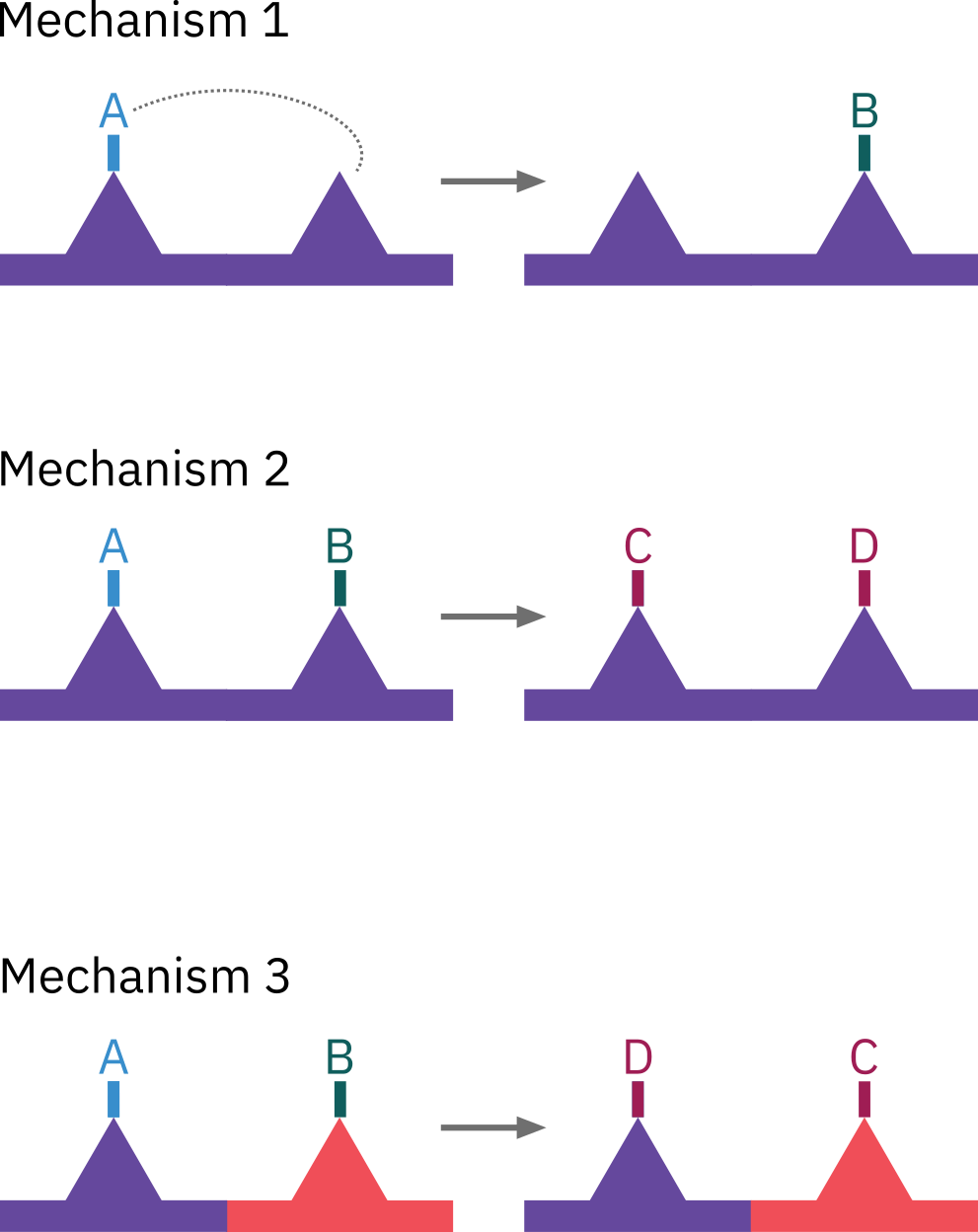
Reactions involving either single- or dual-site mechanisms, are referred to as following Langmuir-Hinshelwood kinetics.

Surface reaction step: Eley-Rideal mechanism

Reaction between adsorbed molecule and a molecule in the gas phase
Unlike the Langmuir-Hinshelwood mechanism it postulates reactions between adsorbed species and molecules directly from the gas phase.
Examples:
- The reaction of propylene and benzene
- Hydrogenation reactions: hydrogen adsorbs on the catalyst surface and reacts with an organic molecule directly striking from the gas phase.

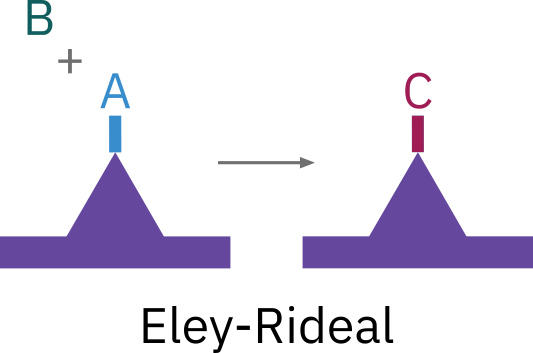
$\ce{A*S + B (g) <=> C*S}$

$r_S = k_S \left( C_{\ce{A*S}} P_B -\frac{C_{\ce{C*S}}}{K_S}\right)$

Desorption step

Products are desorbed into the gas phase

$\ce{C*S <=> C + S}$
Rate of desorption

$r_{DC} = k_D \left( C_{\ce{C*S}} -\frac{P_C C_v}{K_{DC}}\right)$
The desorption of C is the reverse of the adsorption of C

$r_{DC} = - r_{AD,C}$
The desorption equilibrium constant $K_{DC}$ is the reciprocal of the adsorption equilibrium constant $K_C$

$K_{DC} = \frac{1}{K_C}$

$r_{DC} = k_D \left[ C_{\ce{C*S}} - K_C P_C C_v \right ]$

Rate limiting step

When heterogeneous reactions are carried out at steady state, the rates of each of the three reaction steps in series (adsorption, surface reaction, and desorption) are equal to one another

$-r'_A = r_{AD} = r_S = r_D$
One step is usually rate-limiting or rate-controlling
- slowest step among all.
- If the rate-limiting step could be sped up, the entire reaction would be faster
- Although reactions involve all 7 steps, if internal and external mass transfer limitations are removed, only adsorption, surface reaction, or desorption will be rate limiting
- Most of the times, the surface reaction step is rate limiting.

Derive a rate law for catalytic reaction

Postulate catalytic mechanism, and then derive the rate law for that mechanism
Assume pseudo-steady state hypothesis ( $-r'_A = r_{AD} = r_S = r_D$ )
- No accumulation of species on the surface or near interface
- Each species adsorbed on the surface is a reactive intermediate
- Net rate of formation of species i adsorbed on the surface is 0, $r_{\ce{i*S}}=0$
Identify rate limiting step
Steps to derive the rate law
- Select among types of adsorption, surface reaction, and desorption
- Write rate laws for each individual step, assuming all are reversible
- Postulate which step is rate limiting
- Use non-rate-limiting steps to eliminate the surface concentration terms that cannot be measured

The approach in determining catalytic and heterogeneous mechanisms is usually termed the Langmuir-Hinshelwood approach, since it is derived from ideas proposed by Hinshelwood based on Langmuir’s principles for adsorption. The Langmuir-Hinshelwood approach was popularized by Hougen and Watson and occasionally includes their names (LHHW kinetics).

Evaluating a catalytic reaction mechanism

Collect experimental data from test reactor
Postulate and derive equation for rate law using steps in previous slide
See if rate law is consistent with data
If not, then try other surface mechanism (i.e., dual-site adsorption or Eley-Rideal) or choose a different rate-limiting step (adsorption or desorption)
Repeat until the rate expression describes experimental data

Catalyst decay/ deactivation

Solid catalyst activity changes with operation time.
- Catalyst activity usually decreases with operation time (chemical or/and physical reasons).
- sintering, fouling/ coking, poisoning
Catalyst life time is from few minutes to 10 years.
Regeneration of solid catalyst is important
Effects of catalyst decay on solid catalysed reaction
- Conversion, selectivity decreases
- Require higher reaction temperature
- Pressure drop in a fixed bed reactor increases

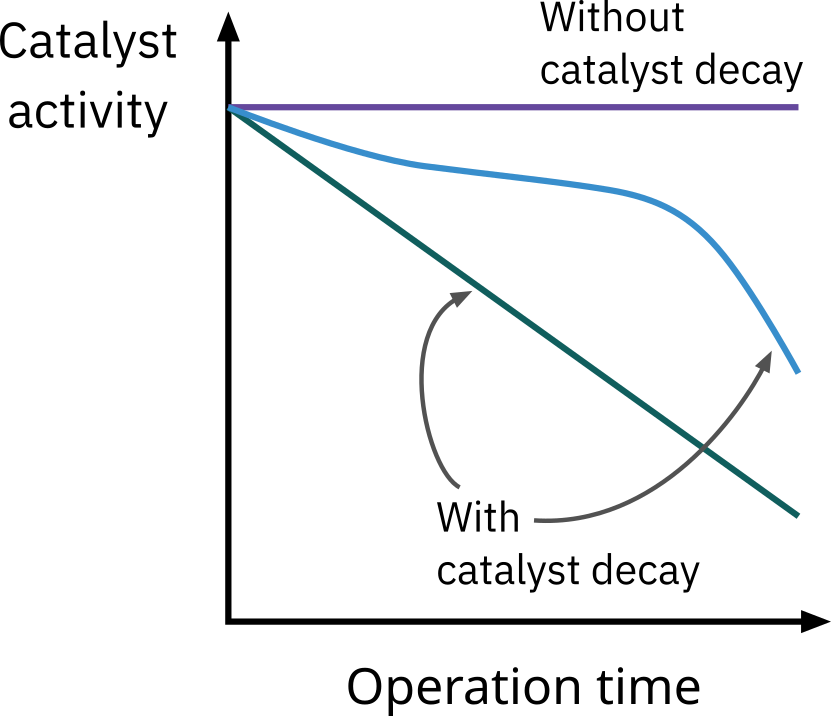
It is very rare to see catalyst activity increases with the operation time

The nickel-based catalysts used in hydroprocessing is often susceptible to sulfur poisoning. However, certain conditioning processes involving controlled exposure to sulfur compounds can rearrange the surface structure, enhancing the catalyst’s activity or selectivity over time.

Sintering

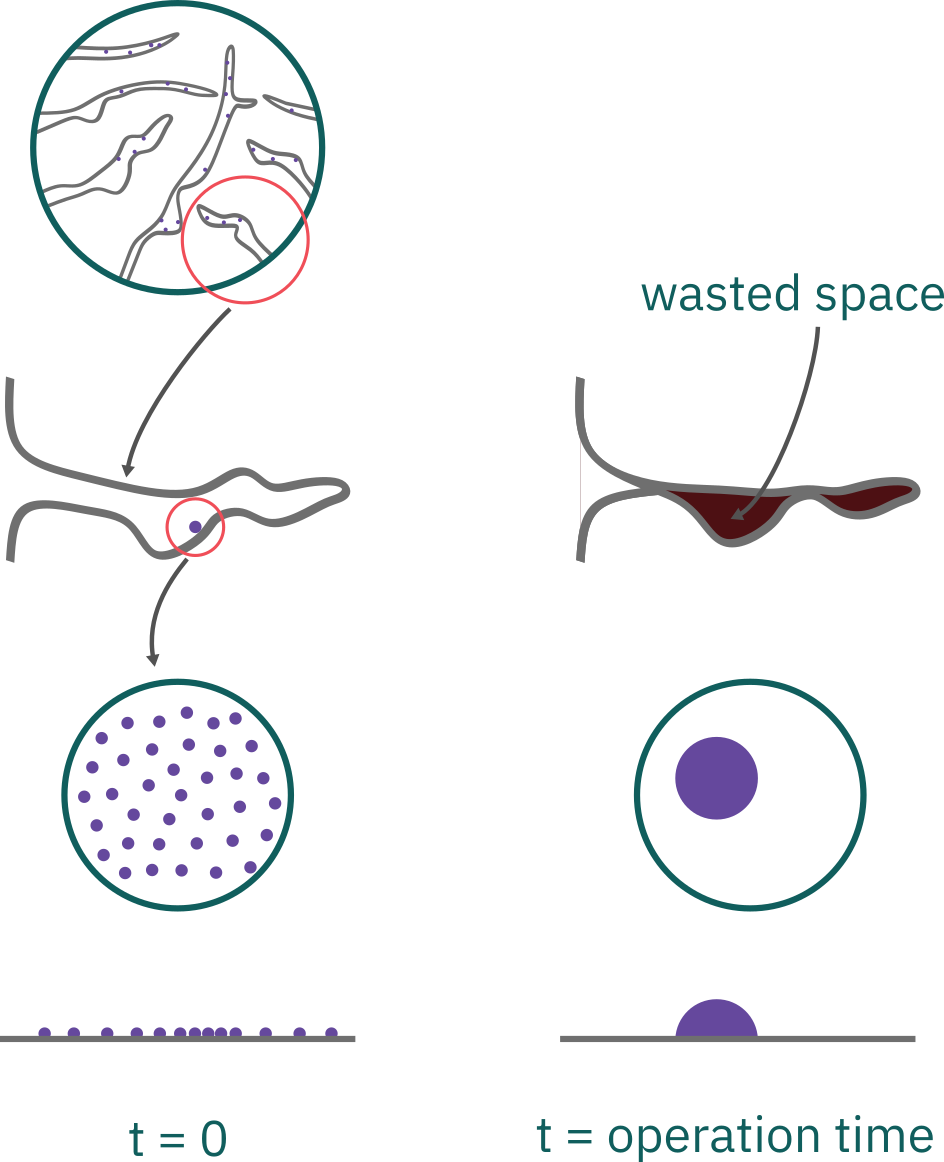
Amount of sintering is usually measured in terms of active surface area of the catalyst $S_a$

$S_a(t) = \frac{S_{a0}}{1 + k_d t}$

Loss of catalytic activity due to a loss of active surface area
- growth of the metals deposited on the support
- narrowing or closing of the pores inside the catalyst pellet
Decay law is second order with respect to the present activity

$r_d = k_d a^2 = - \frac{da}{dt}$

Integrating with $a = 1$ at time $t=0$ for constant $k_d$

$a(t) = \frac{1}{1 + k_d t}$
The sintering decay constant follows Arrhenius equation

$k_d = k_d (T_0) \exp \left[ \frac{E_d}{R} \left( \frac{1}{T_0} - \frac{1}{T} \right) \right ]$

Fouling/ Coking

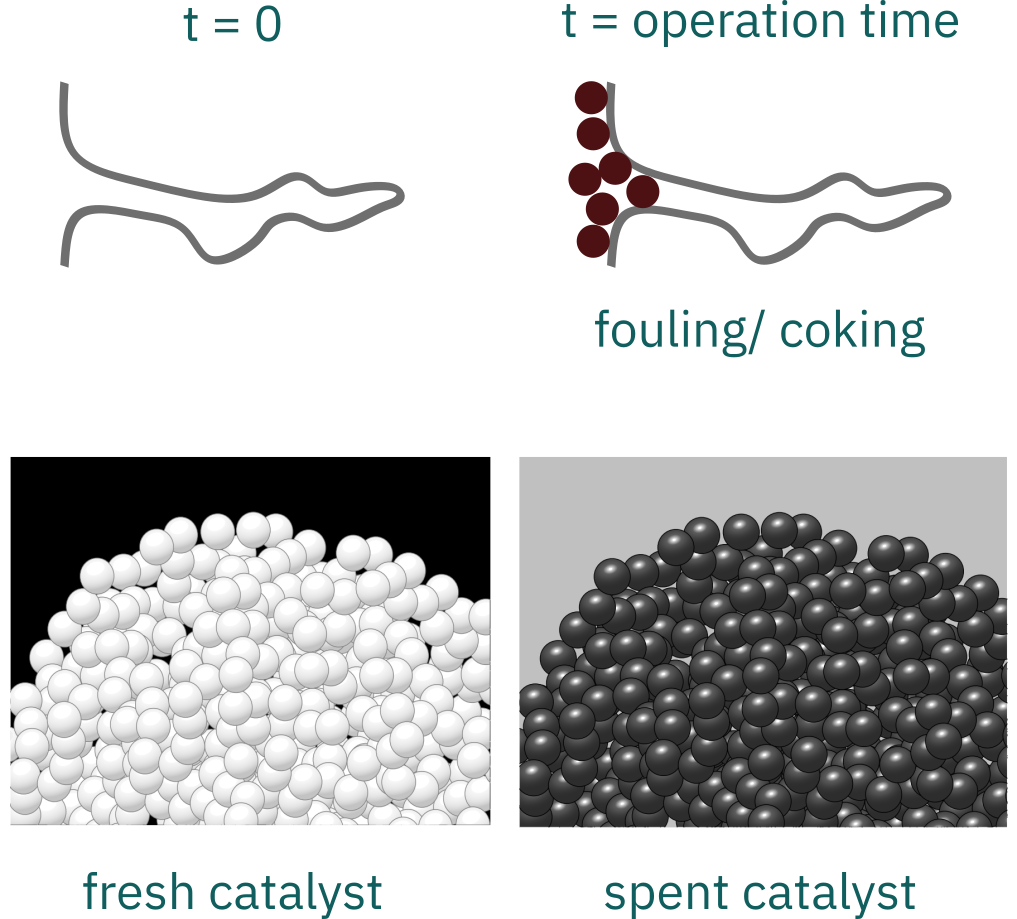
When possible, coking can be reduced by running at elevated pressures (2000–3000 kPa) and hydrogen-rich streams.

Catalysts deactivated by coking can usually be regenerated by burning off the carbon.

Results of carbonaceous (coke) material deposited on the surface of a catalyst
This mechanism is common to reactions involving hydrocarbons.
The amount of coke on the surface after a time t

$C_C = A t^n$

For cracking of crude oil in fixed bed

$C_C = 0.52 t^{0.38}$
Empirical relationships between $a$ and $C_C$

$\begin{aligned} a &=& \frac{1}{k_{Ck} C_C^p + 1} \\ a &=& e^{-\alpha_1 C_C} \\ a &=& \frac{1}{1 + \alpha_2 C_C} \end{aligned}$

Poisoning

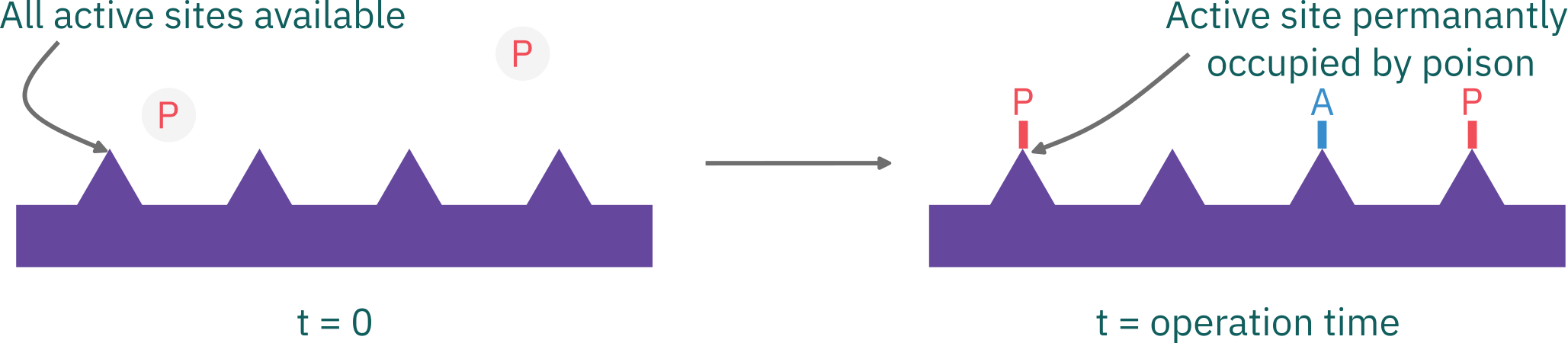
The poisoning molecules become irreversibly chemisorbed to active sites
Reduces the number of sites available for the main reaction.
The poisoning molecule, P, may be a reactant and/or a product in the main reaction, or it may be an impurity in the feed stream.

$\text{Main reaction:} \left\{ \begin{array}{ll} \ce{A + S <=> A*S} \\ \ce{A*S <=> B*S + C(g)} \\ \ce{B*S <=> B + S} \end{array} \right\} \quad -r'_{A} = a(t) \frac{k_{A} C_{A}}{1 + K_{A} C_{A} + K_{B} C_{B}}$

$\text{Poisoning reaction:} \qquad \ce{P + S -> P*S} \qquad -r'_{d} = -\frac{da}{dt} = k'_d C_p^m a^q$

Poisoning

Rate of depletion of the poison from the reactant gas stream onto the catalyst sites, $r_{\ce{P*S}}$ , is proportional to the number of sites that are unpoisoned ( $C_{t0} - C_{\ce{P*S}}$ ) and the concentration of poison in the gas phase is $C_P$

$r_{\ce{P*S}} = k_d (C_{t0} - C_{\ce{P*S}}) C_P$
This rate is also equal to the rate of removal of total active sites ( $C_t$ ) from the surface

$- \frac{dC_t}{dt} = \frac{dC_{\ce{P*S}}}{dt} = r_{\ce{P*S}} = k_d (C_{t0} - C_{\ce{P*S}}) C_P$
Dividing through by $C_{t0}$ $\frac{df}{dt} = k_d (1 - f) C_P \qquad f: \text{fraction of sites that have been poisoned}$
The fraction of sites available for adsorption $(1 - f)$ is the activity $a(t)$

$-\frac{da}{dt} = a(t) k_d C_P$

Decay rate laws

Functional Form of Activity	Decay Reaction Order	Differential Form	Integral Form	Examples
Linear	0	$-da/dt = \beta_0$	$a = 1 - \beta_0 t$	Conversion of para-hydrogen on tungsten when poisoned with O₂
Exponential	1	$-da/dt = \beta_1 a$	$a = e^{-\beta_1 t}$	Ethylene hydrogenation on Cu poisoned with CO; Cracking of gas oil; Vinyl chloride monomer formation
Hyperbolic	2	$-da/dt = \beta_2 a^2$	$1/a = 1 + \beta_2 t$	Cyclohexane dehydrogenation on Pt/Al₂O₃; Isobutylene hydrogenation on Ni
Reciprocal power	-	$-da/dt = \beta_3 a^{1/5}$	$a = A_0 t^{-\beta_3}$	Cracking of gas oil and gasoline on clay