CRE | Chemical Reaction Engineering

Introduction

Usually, more than one reaction occurs within a chemical reactor
Minimization of undesired side reactions that occur with the desired reaction contributes to the economic success of a chemical plant
Goal: determine the reactor conditions and configuration that maximizes product formation
Reactor design for multiple reactions
- Parallel reactions
- Series reactions
- Independent reactions
- More complex reactions
Use of selectivity factor to select the proper reactor that minimizes unwanted side reactions

With multiple reactions, either molar flow or number of moles must be used in setting up the balance equations (no conversion!)

Isothermal reactions in PBR: molar flow rates

Second order reaction $\ce{aA + bB -> cC + dD}$

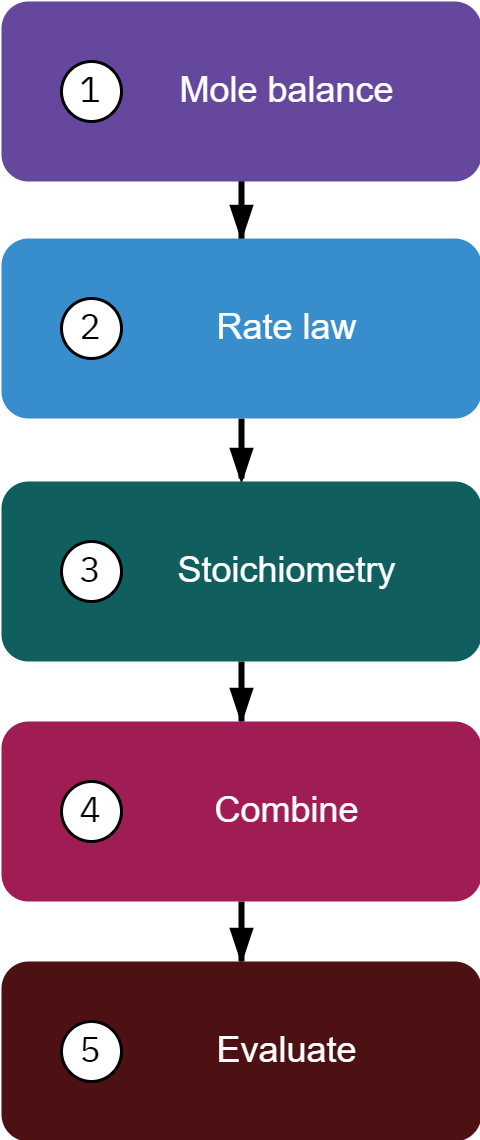
Mole balance: Write balance for each species $i = 1 \ to \ N$

$\frac{dF_i}{dW} = r'_i$
Rate law

$-r'_A = kC_A^\alpha C_B^\beta; \qquad \frac{r'_A}{-a} = \frac{r'_B}{-b} = \frac{r'_C}{c} = \frac{r'_D}{d}$
Stoichiometry $C_i = \frac{C_{A0} (\Theta_i + \nu_i X)} {(1 + \epsilon X)} \left( \frac{P}{P_0} \right) \left( \frac{T_0}{T} \right)$

Pressure: $\frac{dP}{dW} = -\frac{\alpha}{2p} \left( \frac{T}{T_0} \right) \frac{F_T}{F_{T0}}$

Total molar flow rate: $F_T = \sum_{i=1}^N F_i$
Combine:

Collate all equations from steps 1 to 3 to yield a system of equations
Evaluate:

Use ODE solver to solve the system of equations obtained in step 4.

Parallel reactions

Competing reactions
Reactant is consumed by two different pathways to form different products

$\ce{A ->[k_1] D} \\ \ce{A ->[k_2] U}$
Examples
- Ethylene oxidation
  
  $\begin{align*} \ce{C2H4 + O2} & \ce{-> C2H4O} && \text{ethylene oxide} \\ \\ \ce{C2H4 + O2 } & \ce{-> 2 CO2 + 2 H2O} && \text{complete combustion} \end{align*}$
- Fischer Tropsch synthesis
  
  $\begin{align*} \ce{CO + 3 H2 } & \ce{->[k_1] CH4 + H2O} \\ \\ \ce{CO + 2 H2 } & \ce{->[k_2] [C_nH_{2n}]_n + H2O} \end{align*}$

Series reactions

Consecutive reactions
Reactions where reactant forms an intermediate product, which reacts further to form another product.

$\ce{A ->[k_1] D ->[k_2] U} \qquad$
Example
- Ethylene oxide (EO) + Ammonia
$\begin{align*} \ce{C2H4O + NH3} & \ce{-> (HOCH2CH2)NH2} && \text{(mono ethanolamine)}\\ \\ \ce{(HOCH2CH2)NH2 + C2H4O} & \ce{->} \underset{\textcolor{RoyalBlue}{\text{desired product}}}{\ce{(HOCH2CH2)2NH}} && \text{(di ethanolamine)} \\ \\ \ce{(HOCH2CH2)2NH + C2H4O} & \ce{-> (HOCH2CH2)3N} && \text{(tri ethanolamine)} \end{align*}$

Independent reactions

Reactions that occur at the same time
Neither the products nor the reactants react with themselves or one another

$\ce{A ->[k_1] D} \\ \ce{C ->[k_2] U}$
Example: Cracking of crude oil

Hundreds of reactions

$\begin{align*} \ce{C15H32} & \ce{-> C12H26 + C3H6 }\\ \\ \ce{C8H18} & \ce{-> C6H14 + C2H2 } \end{align*}$

Complex reactions

Multiple reactions involving a combination of series, parallel, and/or independent reactions

$\begin{align*} \ce{A + B} & \ce{->[k_1] C + D} \\ \ce{A + C } & \ce{->[k_2] E} \\ \ce{E } & \ce{->[k_3] G} \end{align*}$
Example: Formation of butadiene from ethanol

$\begin{align*} \ce{C2H5OH} & \ce{-> C2H4 + H2O }\\ \\ \ce{C2H5OH} & \ce{-> CH3CHO + H2 }\\ \\ \ce{C2H4 + CH3CHO} & \ce{-> C4H6 + H2O } \end{align*}$

Desired and undesired reactions

Parallel reactions $\begin{align*} \ce{A} & \ce{-> D } && \leftarrow \text{desired product}\\ \\ \ce{A} & \ce{-> u } && \leftarrow \text{undesired byproduct}\\ \end{align*}$
Series reactions $\ce{A ->} \underset{\text{desired product}}{\ce{B}} \ce{-> U}$
Minimize formation of U and maximize formation of D

Greater the amount of U $\leftarrow$ lower production of desired product, higher cost of separation $\leftarrow$ lower profits

Instantaneous selectivity ( $S$ )

Instantaneous selectivity of D with respect to U is the ratio of the rate of formation of D to the rate of formation of U

$S_{D/U} = \frac{r_D}{r_U} = \frac{ \text{rate of formation of D}}{ \text{rate of formation of U}}$

Gives insights in choosing reactors, operating conditions, and reaction schemes that will maximize profit.
Used to guide initial selection of reactor system.
Final selection is made after calculating the overall selelctivity for the reactor and operating conditions chosen.

Overall selectivity ( $\bar{S}$ )

$\bar{S}_{D/U} = \frac{F_D}{F_U} = \frac{ \text{Exit molar flow rate of D}}{ \text{Exit molar flow rate of U}}$

For CSTR:

$F_D = r_D V$

$F_U = r_U V$

$\therefore F_D/F_U = r_D/r_U = S_{D/U} = \bar{S}_{D/U}$
For batch reactor:

$\bar{S}_{D/U} = N_D/N_U$

$N_D, N_U$ : Number of moles of D and U at the end of the reaction.

Yield (Y)

Instantaneous yield ( $Y_D$ )

Ratio of the reaction rate of a given product to the reaction rate of key reactant A

$Y_D = \frac{r_D}{-r_A} = \frac{ \text{Rate of formation of D}}{ \text{Rate of consumption of A}}$

Overall yield ( $\bar{Y}_D$ )

Ratio of moles of product formed at the end of the reaction to the number of moles of the key reactant A, that have been consumed.

$\bar{Y}_{D} = \underset{\text{For CSTR}}{\frac{F_D}{F_{A0} - F_A}} = \underset{\text{For batch reactor}}{\frac{N_D}{N_{A0} - N_A}}$

Overall selectivities ( $\bar{S}$ ) and yields ( $\bar{Y}$ ) are important in determining profits

Conversion ( $X$ )

Gives insight into problem
Often conflicts with selelctivity
- Ideal world $\Rightarrow$ make as much D as possible simultaneously minimize U
- Practical experiece $\Rightarrow$ Greater the conversion, more the undesired product
Not used in solving multiple reaction problems, but calculated later for analysis
For species A $X_A = \underset{\text{Flow system}}{\frac{F_{A0} - F_A}{F_{A0}}} \qquad X_A = \underset{\text{Batch system}}{\frac{N_{A0} - N_A}{N_{A0}}}$
For species B $X_B = \underset{\text{Flow system}}{\frac{F_{B0} - F_B}{F_{B0}}} \qquad X_B = \underset{\text{Batch system}}{\frac{N_{B0} - N_B}{N_{B0}}}$

Derive expression for conversion for a semibatch system where B is fed to A

Algorithm for multiple reactions

Number each and every reaction separately.
Mole balance on each and every species.

$F_{j0} - F_j + \int^V r_j dV = \frac{dN_j}{dt}$
For every reaction write rate law. Calculate the net rate of reaction and relative rates

For component $j$ : $r_j = \sum_{i=1}^N r_{i,j}$
Stoichiometry
Combine:

Collate all equations from steps 2 to 4 to yield a system of equations
Evaluate:

Use ODE solver to solve the system of equations obtained in step 4.

Can be applied to parallel, series, independent, and complex reactions.
For liquid systems concentration is usually preferred variable for mole balance.

Reactor configurations

Parallel reactions: Selectivity

Consider two competing reactions

$\begin{align*} \ce{A -> D} & \text{(desired)} \qquad && r_D = k_D C_A^{\alpha_1}\\ \\ \ce{A -> U} & \text{(undesired)} \qquad && r_U = k_U C_A^{\alpha_2} \end{align*}$
Net rate of disappearance of A

$-r_A = r_D + r_U= k_D C_A^{\alpha_1} + k_U C_A^{\alpha_2}$

$S_{D/U} = \frac{r_D}{r_U} = \frac{k_D}{k_U} C_A^{\alpha_1 - \alpha_2}$

$\alpha_1$ , $\alpha_2$ are positive orders

Case 1: $\alpha_1 > \alpha_2$

$\alpha_1 - \alpha_2 = a$
$S_{D/U} = \frac{k_D}{k_U} C_A^{a}$
To maximize selectivity we wan to carry out the reaction in a manner that will keep $C_A$ as high as possible during the reaction.
Use PFR or batch reactor
Gas phase: Use high pressure, run without inerts
Liquid phase: minimize diluent

Case 2: $\alpha_1 < \alpha_2$

$\alpha_2 - \alpha_1 = b$
$S_{D/U} = \frac{k_D}{k_U} \frac{1}{C_A^{b}}$
To maximize selectivity we wan to carry out the reaction in a manner that will keep $C_A$ as low as possible during the reaction.
Use CSTR or dilute feed stream
Recycle reactor
- Product stream can act as a diluent

Effect of temperature

Need information on activation energy
Sensitivity to temperature for fixed concentrations ( $C_A^a$ is constant)

$S_{D/U} \approx \frac{k_D}{k_U} = \frac{A_D}{A_U} e^{-[(E_D - E_U)/RT]}$

$E_D > E_U$
- $k_D$ increases more rapidly than $k_U$ with increase in temperature
- Perform the reaction at highest possible temperature
$E_D < E_U$
- $k_U$ increases more rapidly than $k_D$ with increase in temperature
- Reaction should be carried out at lower temperature to maximize $S_{D/U}$
- The temperature should not be very low as it might affect reaction extent. Reaction may not proceed at low temperature.

Two simultaneous reactions and two reactants

Consider two competing parallel reactions

$\begin{align*} \ce{A + B -> D} & \text{(desired)} \qquad && r_D = k_D C_A^{\alpha_1} C_B^{\beta_1}\\ \\ \ce{A + B -> U} & \text{(undesired)} \qquad && r_U = k_U C_A^{\alpha_2} C_B^{\beta_2} \end{align*}$
Net rate of disappearance of A

$-r_A = r_D + r_U= k_D C_A^{\alpha_1} C_B^{\beta_1} + k_U C_A^{\alpha_2} C_B^{\beta_2}$
Selectivity

$S_{D/U} = \frac{r_D}{r_U} = \frac{k_D}{k_U} C_A^{\alpha_1 - \alpha_2} C_B^{\beta_1 - \beta_2}$

Selectivity depends on the orders $\alpha_1$ , $\alpha_2$ , $\beta_1$ , $\beta_2$
Several reactor combinations exist

Two simultaneous reactions and two reactants

$\alpha_1 - \alpha_2 = a; \beta_1 - \beta_2 = b$

$\alpha_1 > \alpha_2$ ; $\beta_1 > \beta_2$

$S_{D/U} \propto C_A^{a} C_B^{b}$

Use high $C_A, C_B$
Configurations:
- Tubular reactor
- Batch reactor
- High pressure (gas phase)
- Reduce inerts

$\alpha_1 > \alpha_2$ ; $\beta_1 < \beta_2$

$S_{D/U} \propto \frac{C_A^{a}}{C_B^{b}}$

Use high $C_A$ , low $C_B$
Configurations:
- Semi batch reactor with B fed slowly into large amt of A
- Membrane / tubular reactor with side stream of B continually fed into the reactor
- Series of small CSTRs (A is fed only to the first reactor, B is fed to each reactor)

Two simultaneous reactions and two reactants

$\alpha_1 - \alpha_2 = a; \beta_1 - \beta_2 = b$

$\alpha_1 < \alpha_2$ ; $\beta_1 > \beta_2$

$S_{D/U} \propto C_B^{b} C_A^{a}$

Use high $C_B$ , low $C_A$
Configurations:
- Semi batch reactor with A fed slowly into large amt of B
- Membrane / tubular reactor with side stream of A continually fed into the reactor
- Series of small CSTRs (B is fed only to the first reactor, A is fed to each reactor)

$\alpha_1 < \alpha_2$ ; $\beta_1 < \beta_2$

$S_{D/U} \propto \frac{1}{C_A^{a} C_B^{b}}$

Use low $C_A, C_B$
Configurations:
- CSTR
- Feed diluted streams with inerts
- Low pressure (gas phase)
- Tubular reactor with large recycle ratio
  
  Can be used for highly exothermic reactions. The recycle stream is cooled and returned to the reactor to dilute and cool inlet stream.
  Such configuration helps in avoiding hotspots and runaway reactions.

Reactions in series

The most important variable is time
- Batch time (real time)
- Space time (continuous reactor)
Consider: $\ce{A ->[k_1] B ->[k_2] C}$ .

B is the desired product
If $k_1 \ll k_2$ : First reaction is slow
- Extremely difficult to produce significant amount of B.
If $k_1 \gg k_2$ : First reaction is fast
- Large yield of B can be achieved.

If reaction is allowed to proceed for a long time, desired product B will be converted to undesired product C.

Accuracy of prediction for time required to carry out the reaction is vital.

Reactions in series

Consider the reaction

$\ce{A ->[k_1] B ->[k_2] C}$ .

B is the desired product, C is waste product.
We are interested in
- Concentration vs. time profile
- Maximum concentration of B
- Quench time (time to stop when $C_B$ is maximum)
- Overall selectivity and yield.
Number of reactions

The series reaction can be written as two reactions

$\ce{A -> B}; -r_{1A} = k_1 C_A$ .

$\ce{B -> C}; -r_{2B} = k_2 C_B$ .

Mole balance $\frac{dN_i}{dt} = r_i V$
For constant volume batch reactor

$\frac{dC_A}{dt} = r_A = -k_1 C_A \tag{1}$

$\frac{dC_B}{dt} = r_B = k_1 C_A - k_2 C_B \tag{2}$

$\frac{dC_C}{dt} = r_C = k_2 C_C \tag{3}$

Solve Equation 1, Equation 2, and Equation 3 simultaneously to obtain concentration profile.

Multiple reactions