Collection and analysis of rate data

Chemical Reaction Engineering

Table of contents

  • Rate data analysis
  • Analysis methods

Rate data analysis

  • Isothermal reactor design algorithm

Isothermal reactor design algorithm

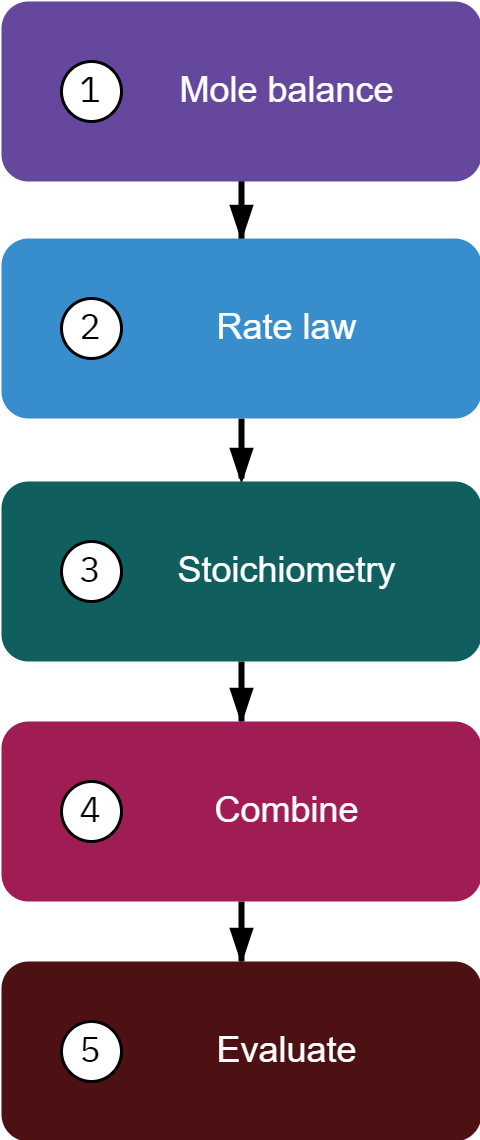
  1. Mole balance

    FA0−FA=∫VrAdV=dNAdt F_{A0} - F_A = \int^V r_A dV = \frac{dN_A}{dt} FA0​−FA​=∫VrA​dV=dtdNA​​

  2. Rate law

    If −rA-r_A−rA​ is given as f(X)f(X)f(X) →\rightarrow→ directly solve the design equations

  3. Stoichiometry

    If −rA=g(C)-r_A = g(C)−rA​=g(C) →\rightarrow→ use stoichiometry to write −rA=f(X)-r_A = f(X)−rA​=f(X)

  4. Combine

    Gather all equations to obtain a system of equations that must be solved.

  5. Evaluate

    The system of equation scan be solved analytically, graphically, numerically, or using software

Isothermal reactor design: molar flow rates

  • In many instances it is easier to work with molar flow rates/ no. of moles than conversion

    • Reactors with external mass transfer (such as membrane reactors)
    • Multiple reactions in gas phase

  • We must write a mole balance for each and every species as opposed to just one species

  • Usually this leads to a system of (simultaneous or) ordinary differential equations

  • Solve the combined set of equations using ODE solver (such as scipy.integrate.solve_ivp)

Isothermal reactions in PBR: molar flow rates

Second order reaction a A+b B→c C+d D\ce{aA + bB -> cC + dD}aA+bB​cC+dD

  1. Mole balance: Write balance for each species i=1 to Ni = 1 \ to \ Ni=1 to N

    dFidW=ri′ \frac{dF_i}{dW} = r'_i dWdFi​​=ri′​

  2. Rate law

    −rA′=kCAαCBβ;rA′−a=rB′−b=rC′c=rD′d -r'_A = kC_A^\alpha C_B^\beta; \qquad \frac{r'_A}{-a} = \frac{r'_B}{-b} = \frac{r'_C}{c} = \frac{r'_D}{d} −rA′​=kCAα​CBβ​;−arA′​​=−brB′​​=crC′​​=drD′​​

  3. Stoichiometry Ci=CA0(Θi+νiX)(1+ϵX)(PP0)(T0T) C_i = \frac{C_{A0} (\Theta_i + \nu_i X)} {(1 + \epsilon X)} \left( \frac{P}{P_0} \right) \left( \frac{T_0}{T} \right) Ci​=(1+ϵX)CA0​(Θi​+νi​X)​(P0​P​)(TT0​​)

    Pressure: dPdW=−α2p(TT0)FTFT0\frac{dP}{dW} = -\frac{\alpha}{2p} \left( \frac{T}{T_0} \right) \frac{F_T}{F_{T0}}dWdP​=−2pα​(T0​T​)FT0​FT​​

    Total molar flow rate: FT=∑i=1NFiF_T = \sum_{i=1}^N F_iFT​=∑i=1N​Fi​

  4. Combine:

    Collate all equations from steps 1 to 3 to yield a system of equations

  5. Evaluate:

    Use ODE solver to solve the system of equations obtained in step 4.

Reactor design problem

  • In practice, collection and analysis of rate data is the most time consuming task in reactor design

  • Data collection is done in the lab, where we can simplify mole balance, stoichiometry, and fluid dynamic considerations

Rate law

  • Algebraic equation that relates −rA-r_A−rA​ to species concentration

    −rA=kA(T)f(CA,CB,...) -r_A = k_A(T) f(C_A, C_B, ...) −rA​=kA​(T)f(CA​,CB​,...)

  • Power law model

    • Most common general forms of the rate law

    −rA=kACAαCBβ -r_A = k_A C_A^\alpha C_B^\beta −rA​=kA​CAα​CBβ​

  • Order of reaction: the powers to which the concentrations are raised

    • The reaction is α\alphaα order with respect to A and β\betaβ order with respect to B.
    • Overall order of reaction n=α+βn = \alpha + \betan=α+β.

  • kAk_AkA​: Specific reaction rate

    • Depends on the temperature

  • Need to determine kkk, α\alphaα, and β\betaβ

Collection and analysis of rate data

  • Goal

    • Determine reaction order, α\alphaα, and specific reaction rate constant, kkk, in the rate law
    • Want ideal conditions →\rightarrow→ well-mixed (data is easiest to interpret) →\rightarrow→ Select a simple reactor

  • Constant-volume batch reactor

    • For homogenous reactions
    • Concentration vs. time measurements
    • Measurement during the unsteady-state operation

  • Differential reactor

    • For solid-fluid reactions
    • Measurement during steady state operation
    • Product concentration is usually monitored for different feed conditions

Algorithm for rate data analysis

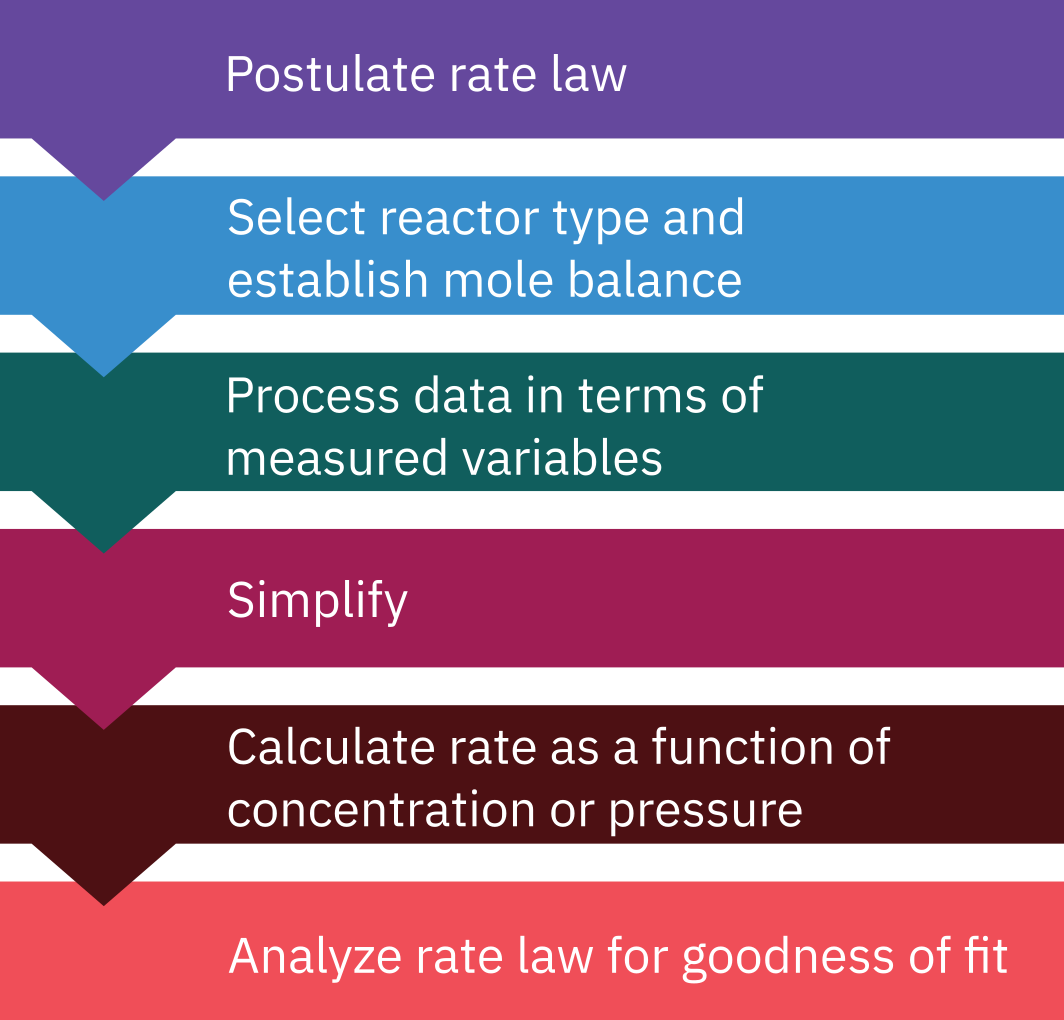
Determination of rate law for homogenous reactions

  • Most often batch reactors are used

    Type of reactor chosen will not affect rate of reaction

  • Batch reactor

    • Simple operations, low cost
    • Ease of sampling, easy clean up, limited waste
    • Uniform concentration can be obtained

  • Mole balance: constant volume −dCAdt=−rA-\frac{dC_A}{dt} = -r_A−dtdCA​​=−rA​

  • Typical measurements
    • Concentration Pressure
    • Temperature: Many times batch reactions are carried out isothermally.
    • Development of heat during reaction: Reaction calorimetry

Method of excess

  • Given concentration vs. time profile in a batch experiment, determine the reaction order and rate constant.

  • A+B→C+D \ce{A + B -> C + D} A+B​C+D

    • Rate law: −rA=kCAαCBβ-r_A = k C_A^\alpha C_B^\beta−rA​=kCAα​CBβ​
    • Need to determine: kkk, α\alphaα, and β\betaβ

  • Determining reaction orders: α\alphaα, and β\betaβ

    • Common simplification: One of the reactants is in excess

    • Two separarate experiments

      • Excess B ⇒\Rightarrow⇒ CB≫CAC_B \gg C_ACB​≫CA​, CBC_BCB​ can be assumed constant. ⇒\Rightarrow⇒ determine α\alphaα.

      • Excess A ⇒\Rightarrow⇒ CA≫CBC_A \gg C_BCA​≫CB​, CAC_ACA​ can be assumed constant. ⇒\Rightarrow⇒ determine β\betaβ.

  • Determining kkk: Measuring rate at known concentrations of A, and B.

Analysis methods

  • Differential analysis
  • Integral analysis
  • Nonlinear regression
  • Method of half life
  • Initial rates method
  • Differential reactor

Differential analysis

  • Irreversible reaction

  • The rate is essentially a function of the concentration of only one reactant.

    A→products;−rA=kCAα\ce{A -> products}; -r_A = k C_A^\alphaA​products;−rA​=kCAα​

  • Isothermal, constant volume batch reactor

  • Mole balance: constant volume −dCAdt=−rA;−rA=kCAα-\frac{dC_A}{dt} = -r_A; -r_A = k C_A^\alpha−dtdCA​​=−rA​;−rA​=kCAα​

  • Taking natural logarithm

ln⁡(−dCAdt)=ln⁡k+αln⁡CA \ln \left( \frac{-dC_A}{dt} \right) = \ln k + \alpha \ln C_A ln(dt−dCA​​)=lnk+αlnCA​

  • Slope of plot of ln⁡[−dCA/dt] vs.ln⁡CA\ln[ -dC_A/dt ] \ \text{vs.} \ln C_Aln[−dCA​/dt] vs.lnCA​ is the reaction order

  • Specific reaction rate can be determined using a specific point ppp: k=(−dCA/dt)p(CA)pαk = \frac{(-dC_A/dt)_p}{(C_A)_p^\alpha}k=(CA​)pα​(−dCA​/dt)p​​

Evaluating −dCAdt\frac{-dC_A}{dt}dt−dCA​​

  • Graphical diffrentiation

    • Very old method
    • Equal area graphical diffrentiation
    • Disparities in the data are easily seen

  • Numerical diffrentiation

    • Finite difference
    • Independent variable (time) is equally spaced

  • Diffrentiation of a polynomial fit to the data

    • Fit a polynomial to CA vs. tC_A \ \text{vs.} \ tCA​ vs. t data

    • e.g. CA=f(t)=a0+a1t+a2t2+a3t3+a4t4C_A = f(t) = a_0 + a_1 t + a_2 t^2 + a_3 t^3 + a_4 t^4CA​=f(t)=a0​+a1​t+a2​t2+a3​t3+a4​t4

    • Analytical derivative

      dCAdt=f′(t)=a1+a2t+a3t2+a4t3\frac{dC_A}{dt} = f'(t) = a_1 + a_2 t + a_3 t^2 + a_4 t^3dtdCA​​=f′(t)=a1​+a2​t+a3​t2+a4​t3

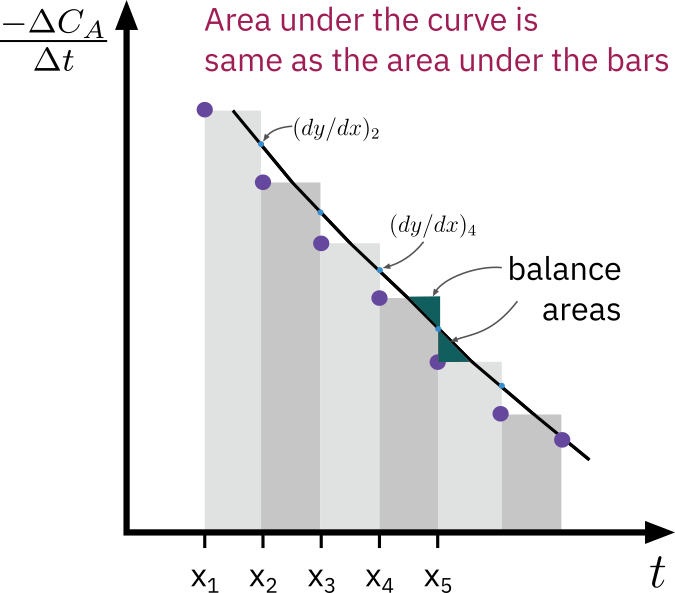
  • Determine reaction order and specific rate from plot of ln⁡[−dCA/dt] vs.ln⁡CA\ln[ -dC_A/dt ] \ \text{vs.} \ln C_Aln[−dCA​/dt] vs.lnCA​

Integral analysis

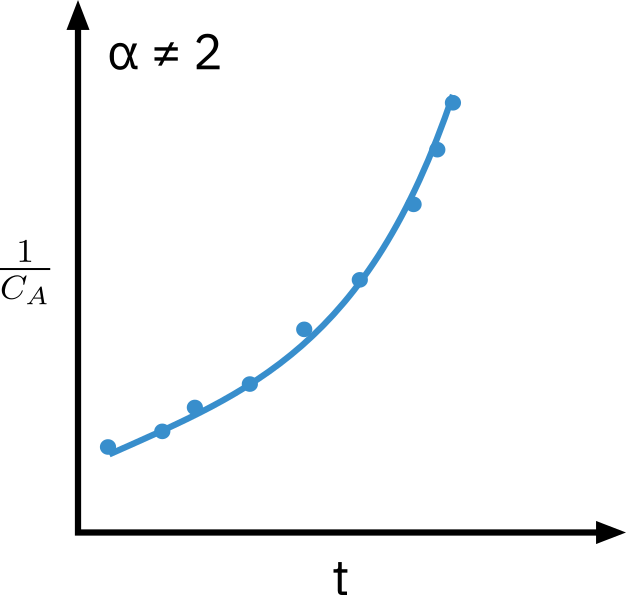
  • Quickest method to determine if the order is 0, 1, or 2.

    ⇒\Rightarrow⇒ Used when reaction order can be guessed or is known.

  1. Guess reaction order

  2. Integate the differential equation to obtain concentration as a function of time

  3. If the guessed order is correct, appropriate plot (determined from integration) should be linear.

Mole balance: −dCA/dt=−rA-dC_A/dt = -r_A−dCA​/dt=−rA​

  • Zero order reaction

    −rA=k-r_A = k−rA​=k

CA=CA0−ktC_A = C_{A0} - ktCA​=CA0​−kt

  • First order reaction

    −rA=kCA-r_A = k C_A−rA​=kCA​

ln⁡CA0CA=kt\ln \frac{C_{A0}}{C_A} = ktlnCA​CA0​​=kt

  • Second order reaction

    −rA=kCA2-r_A = k C_A^2−rA​=kCA2​

1CA=1CA0+kt\frac{1}{C_A} = \frac{1}{C_{A0}} + ktCA​1​=CA0​1​+kt

Need to know appropriate function of concentration corresponding to a rate law that is linear with time.

Integral analysis

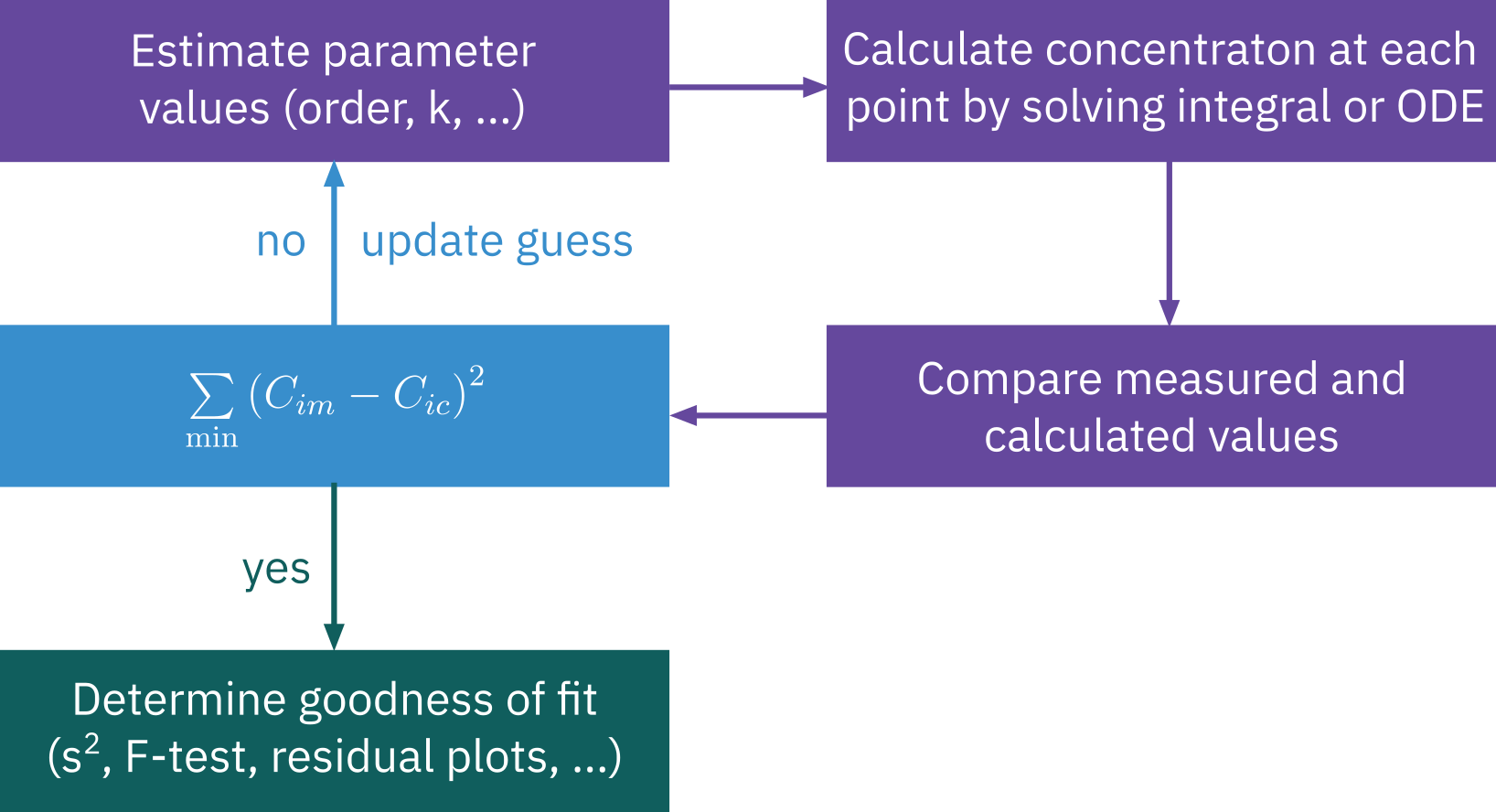
Nonlinear regression

  • Search for parameter values that minimize the sum of squares of the difference between the measured values and calculated values for all data points.

  • Best estimate of parameter values

  • Discriminate between different rate law models

  • Godness of fit

    • Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE)

      Lower values indicate a better fit. RMSE is sensitive to outliers, while MAE provides a more robust error metric.

    • P-value of the F-test in ANOVA (Analysis of Variance)

      A p-value smaller than the significance level (commonly 0.05) indicates that there is a statistically significant relationship.

    • Residual Plots

      Ideally, the residuals should be randomly scattered around 0 across the range of fitted values. Patterns in the residual plot can indicate problems with the model

Method of half life

  • Half life (t1/2t_{1/2}t1/2​): Time taken for the concentration of reactant to fall to half of its initial value.

  • Determine half life as a function of initial concentration

  • Requires several experiments

Reaction: A→products\ce{A -> products}A​products

Rate law: −rA=kCAα-r_A = k C_A^\alpha−rA​=kCAα​

Mole balance: −dCAdt=kCAα -\frac{dC_A}{dt} = k C_A^\alpha −dtdCA​​=kCAα​

  • Integration: CA=CA0C_A = C_{A0}CA​=CA0​ at t=0t = 0t=0

t=1kCA0α−1(α−1)[(CA0CA)α−1−1] t = \frac{1}{k C_{A0}^{\alpha -1} (\alpha -1)} \left[ \left( \frac{C_{A0}}{C_A} \right)^{\alpha -1} -1 \right] t=kCA0α−1​(α−1)1​[(CA​CA0​​)α−1−1]

  • Integration: CA=12CA0C_A = \frac{1}{2} C_{A0}CA​=21​CA0​ at t=t1/2t = t_{1/2}t=t1/2​

t1/2=1kCA0α−1(α−1)[2α−1−1] t_{1/2} = \frac{1}{k C_{A0}^{\alpha -1} (\alpha -1)} \left[ 2^{\alpha -1} -1 \right] t1/2​=kCA0α−1​(α−1)1​[2α−1−1]

  • In general:

t1/n=nα−1−1k(α−1)[1CA0α−1] t_{1/n} = \frac{n^{\alpha -1} -1 }{k (\alpha -1)} \left[ \frac{1}{C_{A0}^{\alpha -1}}\right] t1/n​=k(α−1)nα−1−1​[CA0α−1​1​]

Method of half life

t1/2=1kCA0α−1(α−1)[2α−1−1] t_{1/2} = \frac{1}{k C_{A0}^{\alpha -1} (\alpha -1)} \left[ 2^{\alpha -1} -1 \right] t1/2​=kCA0α−1​(α−1)1​[2α−1−1]

Taking log

ln⁡t1/2=ln⁡2α−1−1(α−1)k+(1−α)ln⁡CA0 \ln t_{1/2} = \ln \frac{2^{\alpha - 1} - 1}{(\alpha -1) k} + (1-\alpha) \ln C_{A0} lnt1/2​=ln(α−1)k2α−1−1​+(1−α)lnCA0​

  • Multiple experiments are performed varying initial concentration and t1/2t_{1/2}t1/2​ is recorded.

  • The plot of ln⁡t1/2\ln t_{1/2}lnt1/2​ vs. ln⁡CA0\ln C_{A0}lnCA0​ is linear with a slope of (1−α)(1 - \alpha)(1−α)

Method of initial rates

  • Perform a series of experiments at different initial concentrations CA0C_{A0}CA0​

  • Determine initial rate of reaction −rA0-r_{A0}−rA0​

  • Determine rate law parameters by relating −rA0-r_{A0}−rA0​ to CA0C_{A0}CA0​

Reaction: A→products\ce{A -> products}A​products

Rate law: −rA=kCAα-r_A = k C_A^\alpha−rA​=kCAα​

Mole balance: −dCAdt=kCAα-\frac{dC_A}{dt} = k C_A^\alpha−dtdCA​​=kCAα​

Initial rate: −rA0=(−dCAdt)0=kCA0α-r_{A0} = \left( \frac{-dC_A}{dt}\right)_0 = k C_{A0}^\alpha−rA0​=(dt−dCA​​)0​=kCA0α​

  • Taking log

ln⁡(−dCAdt)0=ln⁡k+αln⁡CA0\ln \left( \frac{-dC_A}{dt}\right)_0 = \ln k + \alpha \ln C_{A0}ln(dt−dCA​​)0​=lnk+αlnCA0​

Rate data from differential reactors

  • For heterogeneous reactions mostly packed bed reactors (PBRs) are used.

  • Differential reactor: The conversion of the reactants in the bed is extremely small, as is the change in reactant concentration through the bed

  • Reactant concentration through the reactor is essentially constant (i.e. the reactor is considered to be gradient-less)

  • Can treat the mole balance like a CSTR

  • Rate of reaction determined for a specified number of pre-determined initial or entering reactant concentrations

  • Determine rate of reaction as a function concentration or partial pressure

  • Operate isothermally

Differential reactor

  • Assumptions

    • No concentration and temperature gradient (gradientless reactor)
    • High volumetric flow rate
    • Small catalyst particles (No mass transfer limitation)
    • Very low conversion
    • Low/ negligible heat release (isothermal)
    • No bypassing/ channeling (uniform flow across catalyst layer)

  • Mole balance:

    in - out + generation = accumulation

FA0−FAe+rA′ΔW=0 F_{A0} - F_{Ae} + r'_A \Delta W = 0 FA0​−FAe​+rA′​ΔW=0

−rA′=FA0−FAeΔW=υ0CA0−υCAeΔW -r'_A = \frac{F_{A0} - F_{Ae}}{\Delta W} = \frac{\upsilon_0 C_{A0} - \upsilon C_{Ae}}{\Delta W} −rA′​=ΔWFA0​−FAe​​=ΔWυ0​CA0​−υCAe​​

  • For constant flow rate υ=υ0\upsilon = \upsilon_0υ=υ0​

−rA′=υ0CA0XΔW=υ0CPΔW -r'_A = \frac{\upsilon_0 C_{A0} X}{\Delta W} = \frac{\upsilon_0 C_{P}}{\Delta W} −rA′​=ΔWυ0​CA0​X​=ΔWυ0​CP​​

→\rightarrow→ For small conversion −rA′-r'_A−rA′​ can be expressed as a function of CA0C_{A0}CA0​

Chemical Reaction Engineering

1 / 23
Collection and analysis of rate data Chemical Reaction Engineering

  1. Slides

  2. Tools

  3. Close
  • Collection and analysis of rate data
  • Table of contents
  • Rate data analysis
  • Isothermal reactor design algorithm
  • Isothermal reactor design: molar flow rates
  • Isothermal reactions in PBR: molar flow rates
  • Reactor design problem
  • Rate law
  • Collection and analysis of rate data
  • Algorithm for rate data analysis
  • Determination of rate law for homogenous reactions
  • Method of excess
  • Analysis methods
  • Differential analysis
  • Evaluating \frac{-dC_A}{dt}
  • Integral analysis
  • Integral analysis
  • Nonlinear regression
  • Method of half life
  • Method of half life
  • Method of initial rates
  • Rate data from differential reactors
  • Differential reactor
  • f Fullscreen
  • s Speaker View
  • o Slide Overview
  • e PDF Export Mode
  • r Scroll View Mode
  • b Toggle Chalkboard
  • c Toggle Notes Canvas
  • d Download Drawings
  • ? Keyboard Help