Chemical Reaction Engineering
Form of stoichiometric table is virtually identical to batch systems
Replace N_{j0} by F_{j0}
Replace N_{j} by F_{j}
Use algorithm rather than memorizing equations
Mole balance
F_{A0} - F_A + \int^V r_A dV = \frac{dN_A}{dt}
Rate law
If -r_A is given as f(X) \rightarrow directly solve the design equations
Stoichiometry
If -r_A = g(C) \rightarrow use stoichiometry to write -r_A = f(X)
Combine
Gather all equations to obtain a system of equations that must be solved.
Evaluate
The system of equation scan be solved analytically, graphically, numerically, or using software
Fogler, H. Scott. 2016. Elements of Chemical Reaction Engineering. Fifth edition
Mole balance
N_{A0} \frac{dX_A}{dt} = -r_A V
Rate law
-r_A = kC_A
Stoichiometry
C_A = C_{A0}(1-X_A)
Combine
N_{A0} \frac{dX_A}{dt} = k C_{A0} (1 - X_A) V
Evaluate
For constant batch volume V = V_0 solve
N_{A0} \frac{dX_A}{dt} = k C_{A0} (1 - X_A) V_0
Mole balance
V = \frac{F_{A0} X_A}{-r_A}
Rate law
-r_A = kC_A
Stoichiometry
C_A = C_{A0}(1-X_A)
Combine: Put F_{A0} in terms of C_{A0}
V = \frac{\cancel{C_{A0}} \upsilon_0 X_A}{k \cancel{C_{A0}} (1-X_A)}
Evaluate
V = \frac{\upsilon_0 X}{k (1-X)}
Mole balance
V = \frac{F_{A0} X_A}{-r_A}
Rate law
-r_A = kC_A^2
Stoichiometry
C_A = C_{A0}(1-X_A)
Combine: Put F_{A0} in terms of C_{A0}
V = \frac{C_{A0} \upsilon_0 X_A}{k C_{A0}^2 (1-X_A)^2}
Evaluate
\tau = \frac{X}{k C_{A0}(1-X)^2}; \quad X_A=\frac{(1 + 2 \tau k C_{A0}) - \sqrt{1 + 4 \tau k C_{A0}}}{2 \tau k C_{A0}}
X_A=\frac{(1 + 2 Da_2) - \sqrt{1 + 4 Da_2}}{2 Da_2}; \quad Da_2 = \tau k C_{A0}
A first order reaction is carried out isothermally using 2 CSTRs that are the same size, and \upsilon and k are the same in both reactors (\tau_1 = \tau_2 = \tau; k_1 = k_2 = k).
Effluent of reactor 1 is input for reactor 2, no change in \upsilon
For the first CSTR, C_{A1} = \frac{C_{A0}}{1 + \tau k} = k
For second CSTR apply the algorithm
Activity: Exit concentration for CSTR in series
Using the algorithm, obtain C_{A2} in terms of C_{A0} and Da
For n identical CSTRs
C_{An} = \frac{C_{A0}}{(1 + \tau k)^n}
Rate of disappearance in the n^{th} reactor
-r_{An} = k C_{An} = \frac{k C_{A0}}{(1 + \tau k)^n}
\therefore \cancel{k} \cancel{C_{A0}}(1 - X_{An}) = \frac{\cancel{k} \cancel{C_{A0}}}{(1 + \tau k)^n}
X_{An} = 1 - \frac{1}{(1 + Da)^n}
Conversion will be higher than a single reactor of volume V = n V_i.
Volume of each CSTR
V_i = \frac{V}{n} = \frac{\text{total volume of all CSTRs}}{\text{no. of CSTRs}}
Molar flow rate of each CSTR F_{A0,i} = \frac{F_{A0}}{n} = \frac{\text{total molar flow rate}}{\text{no. of CSTRs}}
Mole balance
V_i = F_{A0,i} \left( \frac{X_{Ai}}{-r_{Ai}}\right)
Same T, V, \upsilon
\begin{align*} F_{A0,1} & = F_{A0,2} = \cdots = F_{A0,n} \\ \therefore X_{A1} & = X_{A2} = \cdots = X_{A} \\ \therefore -r_{A1} & = -r_{A2} = \cdots = -r_{A} \end{align*}
\frac{V}{\cancel{n}} = \frac{F_{A0}}{\cancel{n}} \left( \frac{X_{Ai}}{-r_{Ai}}\right); V = F_{A0} \left( \frac{X_{A}}{-r_{A}}\right)
Conversion achieved by any one of the reactors in parallel is the same as if all the reactant were fed into one big reactor of volume V
Mole balance
\frac{dX_A}{dV} = \frac{-r_A}{F_{A0}}
Rate law
-r_A = kC_A
Stoichiometry
C_A = C_{A0}(1-X_A)
Combine: Put F_{A0} in terms of C_{A0}
\frac{dX}{dV} = \frac{k C_{A0} (1 - X_A)}{C_{A0} \upsilon_0}
Evaluate
\frac{\upsilon_0}{k} \int_0^X \frac{dX_A}{(1 - X_A)} = \int_0^V dV ;\quad V = \frac{\upsilon_0}{k} \ln \left( \frac{1}{1 - X} \right)
Activity
Derive equation for conversion in a liquid phase PFR for second order reaction
Gas-phase reactions are usually carried out in tubular reactors (PFRs & PBRs)
C_j = \frac{C_{A0} (\Theta_j + \nu_j X)} {(1 + \epsilon X)} \underset{\color{red}{1}}{\cancel{\left( \frac{P}{P_0} \right)}} \underset{\color{red}{1}}{\cancel{\left( \frac{T_0}{T} \right)}} \underset{\color{red}{1}}{\cancel{\left( \frac{Z_0}{Z} \right)}}
C_j = \frac{C_{A0} (\Theta_j + \nu_j X)} {(1 + \epsilon X)}
Mole balance
\frac{dX_A}{dV} = \frac{-r_A}{F_{A0}}
Rate law
-r_A = kC_A^2
Stoichiometry C_A = \frac{C_{A0} (1 - X)} {(1 + \epsilon X)}
Combine: Put F_{A0} in terms of C_{A0}
\frac{dX}{dV} = \frac{k C_{A0}^2 (1 - X_A)^2}{(1 + \epsilon X)^2 C_{A0} \upsilon_0}
Evaluate
V = \frac{\upsilon_0}{k C_{A0}} \int_0^X \frac{(1 + \epsilon X)^2 }{(1 - X_A)^2} dX_A
\int_0^X \frac{(1 + \epsilon x)^2}{(1 - x)^2} dx = 2\epsilon (1 + \epsilon) \ln(1 - X) + \\ \frac{\epsilon X + (1 + \epsilon)^2 X^2}{1 - X}
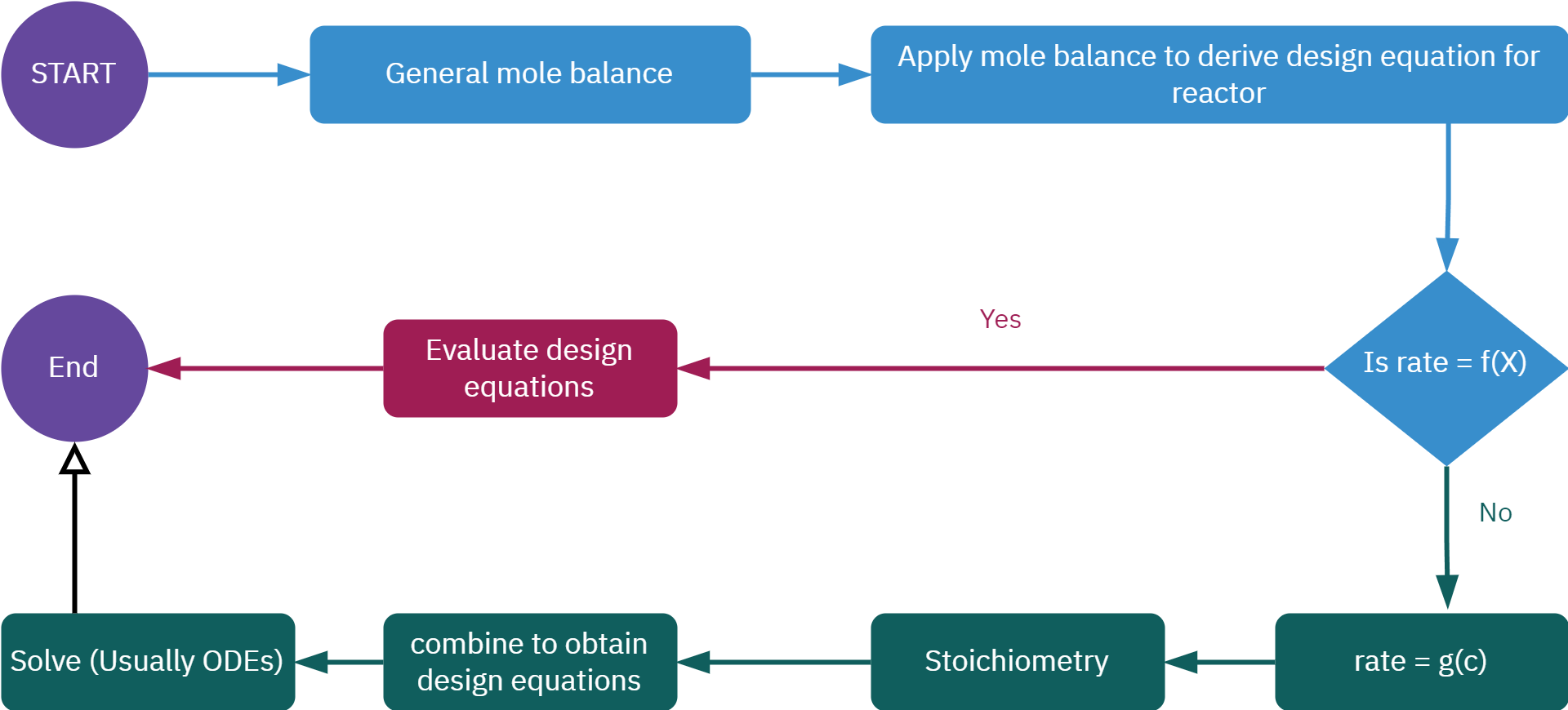
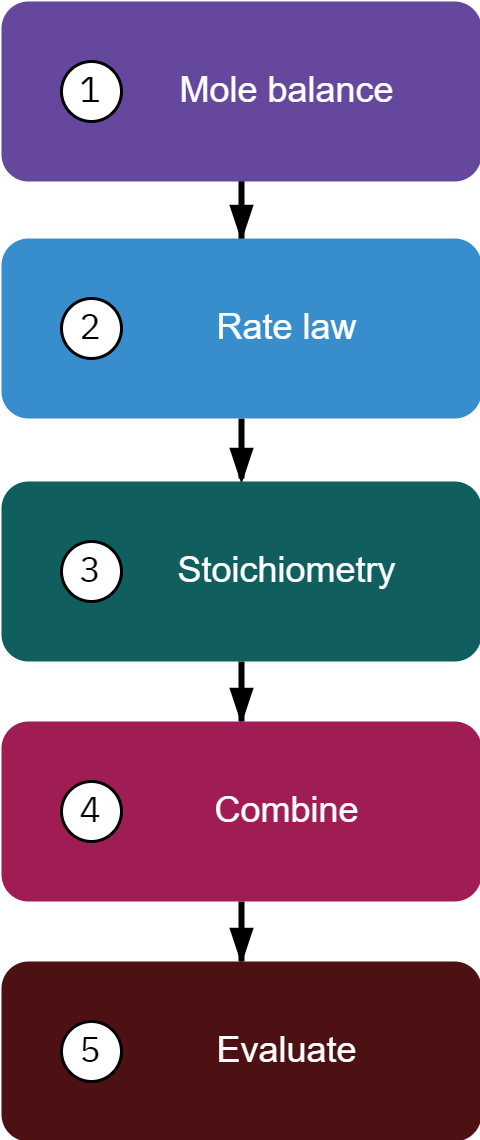
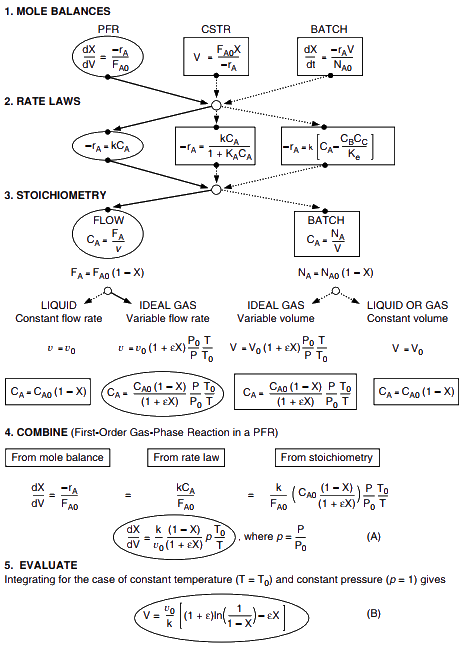
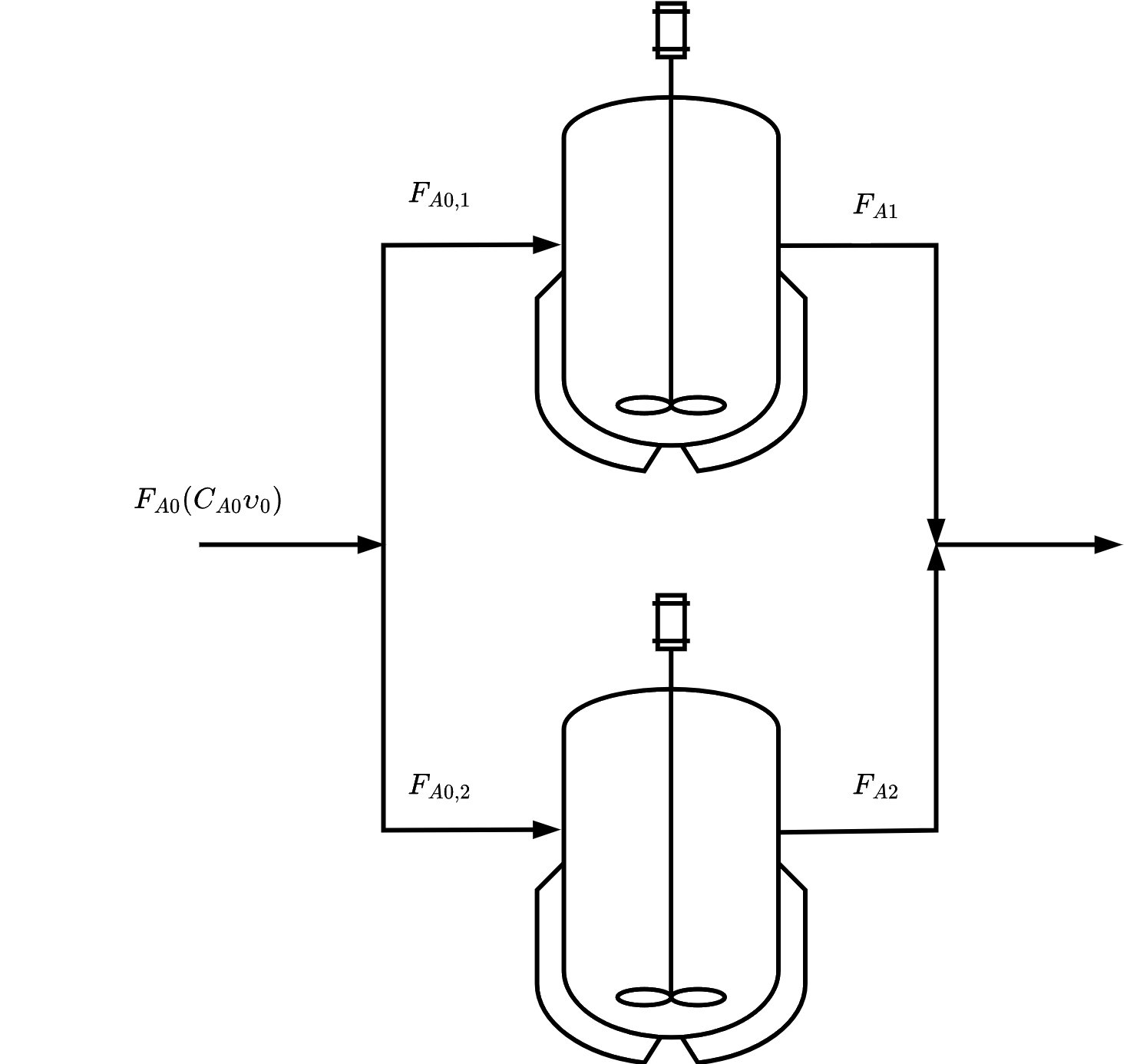
from sympy import symbols, integrate, pprint
# Define the symbols
epsilon, x = symbols('epsilon x', real=True)
X = symbols('X', real=True, positive=True)
integ = (1 + epsilon * x)**2 / (1 - x)**2
integ_result = integrate(integ,(x))
pprint(integ_result) 2
2 ε + 2⋅ε + 1
ε ⋅x + 2⋅ε⋅(ε + 1)⋅log(x - 1) - ────────────
x - 1 V = \frac{\upsilon_0}{k (C_{A0})} [ 2\epsilon(1 + \epsilon) \ln(1 - X_A) + \\ \epsilon^2 X_A + \frac{(1 + \epsilon)^2 X_A^2}{1 - X_A} ]
\epsilon = \frac{N_{Tf} - N_{T0}}{N_{T0}} = \frac{\text{Change in total moles at } X_A = 1}{\text{total moles fed}}
\epsilon: expansion factor- fraction of change in V per mole A reacted
\epsilon = 0: \upsilon = \upsilon_0: Constant volumetric flow rate as X_A increases
\epsilon < 0: \upsilon < \upsilon_0: volumetric flow rate decreases as X_A increases
\epsilon > 0: \upsilon > \upsilon_0: volumetric flow rate increases as X_A increases
Mole balance
\frac{dX_A}{dW} = \frac{-r'_A}{F_{A0}}
Rate law
-r'_A = kC_A^2
Stoichiometry C_A = \frac{C_{A0} (1 - X)} {(1 + \epsilon X)} \left( \frac{P}{P_0} \right)
Combine: Put F_{A0} in terms of C_{A0}
\frac{dX}{dW} = \frac{k C_{A0}^2 (1 - X_A)^2}{(1 + \epsilon X)^2 C_{A0} \upsilon_0} \left( \frac{P}{P_0} \right)^2
Evaluate
\frac{dX}{dW} = \frac{k C_{A0}}{\upsilon_0} \frac{(1 - X_A)^2}{(1 + \epsilon X)^2} \left( \frac{P}{P_0} \right)^2
Mole balance: Write balance for each species i = 1 \ to \ N
\frac{dF_i}{dW} = r'_i
Rate law
-r'_A = kC_A^\alpha C_B^\beta; \qquad \frac{r'_A}{-a} = \frac{r'_B}{-b} = \frac{r'_C}{c} = \frac{r'_D}{d}
Stoichiometry C_i = \frac{C_{A0} (\Theta_i + \nu_i X)} {(1 + \epsilon X)} \left( \frac{P}{P_0} \right) \left( \frac{T_0}{T} \right)
Pressure: \frac{dP}{dW} = -\frac{\alpha}{2p} \left( \frac{T}{T_0} \right) \frac{F_T}{F_{T0}}
Total molar flow rate: F_T = \sum_{i=1}^N F_i
Combine:
Collate all equations from steps 1 to 3 to yield a system of equations
Evaluate:
Use ODE solver to solve the system of equations obtained in step 4.
