Rate law and stoichiometry

Chemical Reaction Engineering

Table of contents

• Rate law
• Stoichiometry

Rate law

Reactor mole balance in terms of X

Reactor	Mole balance
Batch	N_{A0}\frac{dX}{dt} = r_AV
CSTR	V = \frac{F_{A0}X}{-r_A}
PFR	F_{A0}\frac{dX}{dV} = -r_A
PBR	F_{A0}\frac{dX}{dW} = -r'_A

• Rate law

  The algebraic expression for the reaction rate equation, r_j.

  -r_A = f \left[ \begin{array}{c} \text{temperature} \\ \text{dependent} \\ \text{terms} \end{array} , \begin{array}{c} \text{concentration} \\ \text{dependent} \\ \text{terms} \end{array} \right] = f(T, C)]

• How to derive an equation for –r_A in terms of X_A

  • Relate all r_j to C_j \Rightarrow Rate law

  • Relate all C_j to V or \upsilon \Rightarrow Stoichiometry

  • Relate V or \upsilon to X_A \Rightarrow Stoichiometry

  • Put together

    r_A = f(T, X_A)

Basic definitions

• Homogeneous reaction: involves only one phase.

• Heterogeneous reaction: involves more than one phase. Reaction usually occurs at the interface.

• Irreversible reaction: proceeds in only one direction. Continues until one of the reactants is exhausted.

• Reversible reaction: proceeds in either direction. Continues until equilibrium concentration is reached.

  No reaction is completely irreversible. For irreversible reactions equilibrium point lies far to the product side.

• Reaction rate

  • Rate laws: are the algebraic equations that apply to a given reaction

  • Relative rates: how fast one species appears or disappears relative to the other species in a given reaction.

  • Net rate of formation of a given species (e.g., A): is the sum of the rate of the reactions of A for all the reactions in which A is either a reactant or product.

Molecularity of reaction

• Number of atoms, ions, or molecules involved (colliding) in a reaction step

• Unimolecular: One molecule colliding in one reaction step

  • radioactive decay \ce{ _{92}U^{238} -> _{90}Th^{234} + _{2}He^{4} }
  • rate of disappearance of U \Rightarrow -r_U = kC_U

• Bimolecular: Two molecule colliding in one reaction step

  • Only true bimolecular reactions are those involving collision with free radicals \ce{ Br. + C2H6 -> HBr + C2H5.}
  • -r_{\ce{Br.}} = kC_{\ce{Br.}}C_{\ce{C2H6}}

• Trimolecular: Three molecule colliding in one reaction step

  • The probability of trimolecular reaction is almost non-existent

  • In most instances the reaction pathway follows a series of bimolecular reactions.

Relative rates of reaction

• How fast one species appears or disappears relative to the other species in a given reaction.

• Can be obtained from the ratio of stoichiometric coefficients

• Consider a reaction

  \ce{aA + bB -> cC + dD}

• For every mole of A consumed \frac{c}{a} moles of C appear

  r_C = \left[ \begin{array}{c} \text{rate of} \\ \text{formation of C}\end{array} \right] = \frac{c}{a} \left[ \begin{array}{c} \text{rate of} \\ \text{disappearance of A}\end{array} \right] = \frac{c}{a} (-r_A)

  r_C = \frac{-c}{a} r_A Similarly, r_C = \frac{c}{d} r_D

\begin{align*} \ce{A} & \quad + \quad & \ce{\frac{b}{a} B} &\quad \ce{->} \quad & \ce{\frac{c}{a} C} &\quad + \quad & \ce{\frac{d}{a} D} \\ \frac{-r_A}{a} & \quad = \quad & \frac{-r_B}{b} & \quad = \quad & \frac{r_C}{c} & \quad = \quad & \frac{r_D}{d} \end{align*}

Rate law

• The rate of reaction depends on collision frequency of the molecules.

• Concentration and temperature

  • Molecular collision frequency \propto concentration

    \Rightarrow Rate of reaction \propto concentration. -r_A = f(C_A, C_B, ...) \quad \text{for const. T}

  • As temperature increases, collision frequency increases

    \Rightarrow Rate of reaction \propto temperature. -r_A = f([T],[C_A, C_B, ...])

• For many reactions

  -r_A = k_A(T) f(C_A, C_B, ...)

• Specific rate of reaction (rate constant), k_A(T)

  • Proportionality constant in the rate equation

  • Depends on the temperature (following the Arrhenius equation), the presence of a catalyst, and other environmental conditions but is independent of the reactant concentrations.

Power law model

• Dependence of -r_A on concentration of species present (f(C_j)) is almost always determined by experimental observations.

• Functional dependence on concentration may be postulated by theory

  \Rightarrow Experiments are required to confirm the proposed form

• Power law model is most common general forms of the rate law

  -r_A = k_A C_A^\alpha C_B^\beta

• Order of reaction: the powers to which the concentrations are raised

  • The reaction is \alpha order with respect to A and \beta order with respect to B.
  • Overall order of reaction n = \alpha + \beta.

• k_A: Specific reaction rate

  \text{Units of } k_A = \frac{\text{(conc)}^{1-n}}{\text{time}}

Order of reaction

\ce{A -> Products}

Reaction order	Rate equation	Units of k_A
0^{th} order	-r_A = k_A	\{k\} = \frac{mol}{volume \ s}
1^{st} order	-r_A = k_A C_A	\{k\} = \frac{1}{s}
2^{nd} order	-r_A = k_A C_A^2	\{k\} = \frac{volume}{mol \ s}
3^{rd} order	-r_A = k_A C_A^3	\{k\} = \frac{(volume/mol)^2}{s}

Elementary reaction

• A reaction involving single step is called an elementary reaction.

• Stoichiometric coefficients in the reaction are equal to the powers in the rate law.

• \ce{2NO + O2 -> 2NO2}

  This reaction is not elementary, but under some conditions it follows an elementary rate law

  -r_{NO} = k_{NO} C_{NO}^2 C_{O_2}

  \Rightarrow Elementary as written

• \ce{CO + Cl2 -> COCl2}

  This reaction is non-elementary

  -r_{CO} = k_{CO} C_{CO} C_{Cl_2}^{3/2}

  1^{st} order with respect to \ce{CO} and 3/2 order with resect to \ce{Cl2} (5/2 order overall)

  \Rightarrow Non-elementary reaction

Complex rate expression

\ce{2N2O -> 2N2 + O2} \qquad -r_{N_2O} = \frac{ k_{N_2O} C_{N2O}}{1 + k' C_{O_2}}

• Rate expression cannot be separated into solely temperature dependent and concentration dependent terms.

• Overall reaction order cannot be stated

• Only undrer limiting circumstances we can speak of reaction order

  • for 1 >> k'C_{O_2}; -r_{N_2O} = k_{N_2O} C_{N_2O} \Rightarrow ‘Apparent’ first order reaction

  • for 1 << k'C_{O_2}; -r_{N_2O} = k_{N_2O} \frac{C_{N_2O}}{C_{O_2}} \Rightarrow ‘Apparent’ 0^{th} order reaction

    Reaction is -1^{th} order with \ce{O2} and 1^{st} order with \ce{N2O}.

This kind of rate expression is common for liquid and gaseous reactions promoted by solid catalysts.

Heterogeneous reactions

• Historically for many gas-solid catalyzed reactions it is customary to write rate laws in terms of partial pressures rather than concentrations.

• Weight of catalyst is important rather than reactor volume (\Rightarrow -r'_A)

• Hydromethylation of toluene

  \ce{C6H5CH3 + H2 ->[{cat}] C6H6 + CH4}

  -r'_T = \frac{k P_{H_2} P_T}{1 + K_B P_B + K_T P_T}

  • ’ (prime): indicates typical units are in /g-cat
  • P: partial pressures (kPa or atm)
  • K: adsorption constant (1/kPa or atm^{-1})
  • [K] = \frac{mol \ toluene}{kg\ cat \cdot s \cdot kPa^2}

• Use ideal gas law to express the reaction in terms of concentrations: P_i = C_i RT

Reversible reaction

• All rate laws must reduce to thermodynamic relationships relating the reacting species concentrations at equilibrium

• At equilibrium rate of reaction is zero for all the species (-r_A \equiv 0)

• For a reaction \ce{aA + bB <=> cC + dD}

  K_c = \frac{C_{C_e}^c C_{D_e}^d}{C_{A_e}^a C_{B_e}^b} \qquad [K_c] = \left(\frac{mol}{volume}\right)^{c +d -a -b}

• For elementary reaction \ce{A <=>[{k_f}][{k_r}] B}

  -r_A = k \left( C_A - \frac{C_B}{K_c} \right); K_c = \frac{k_f}{k_r}

Equilibrium constant

van’t Hoff equation

When there is no change in number of moles and heat capacity term \Delta C_p = 0

K_c(T) = K_c(T_1) exp \left[ \frac{\Delta H_{Rx}^\circ}{R} \left( \frac{1}{T_1} - \frac{1}{T} \right)\right]

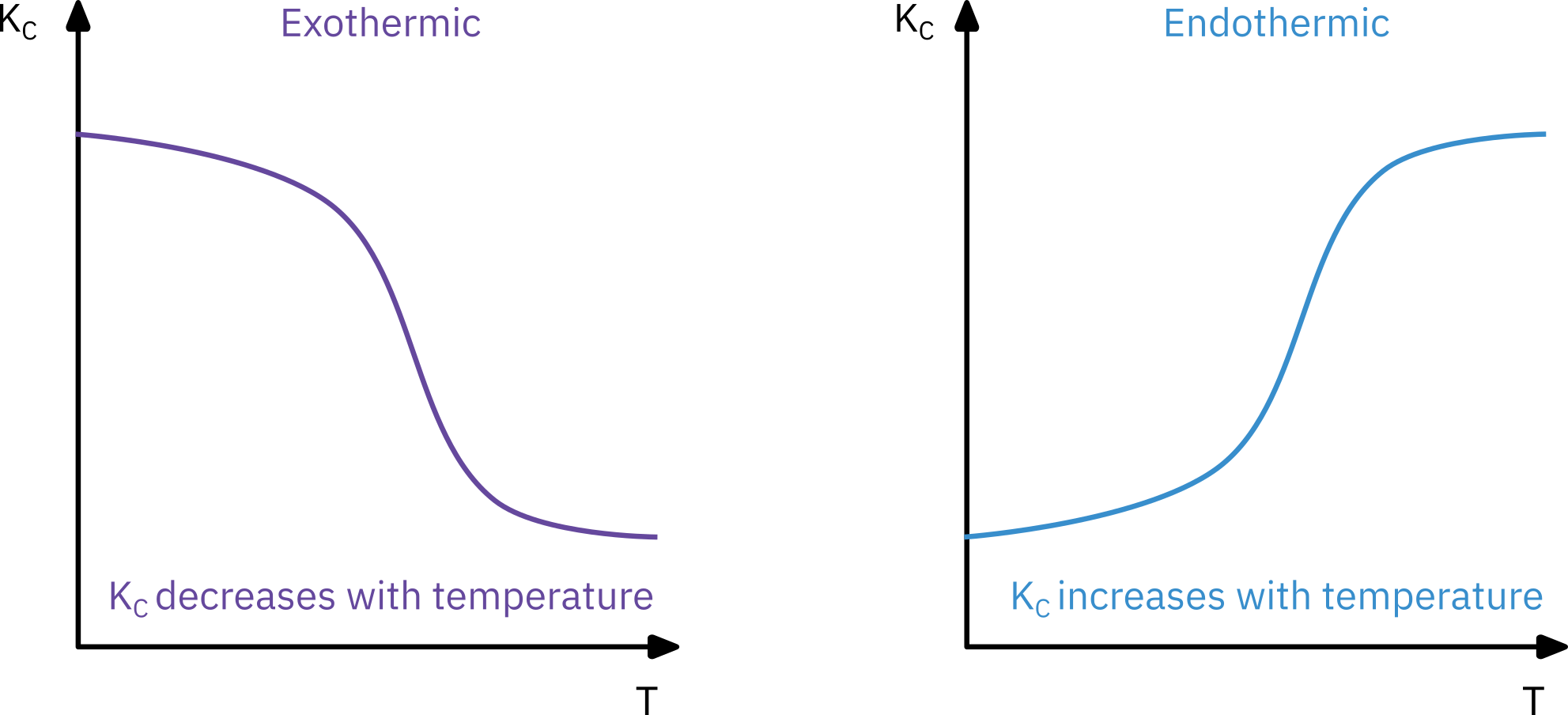
The reaction rate constant (k_A)

\Rightarrow Not a constant. Just independent of concentration

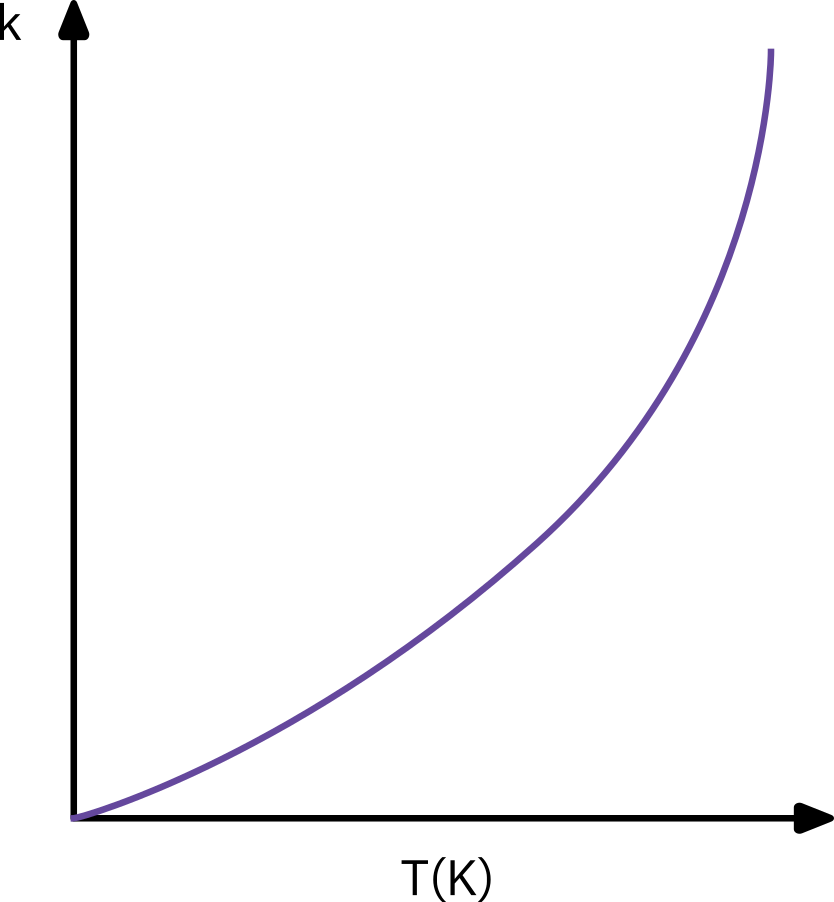
• Arrhenius equation

  k_A(T) = A e^{\frac{-E}{RT}} \Rightarrow k_0 e^{-E/RT}

  • k_0, A: Preexponential factor/ frequency factor
  • E: Activation energy (J/mol) or (cal/mol)
  • R: Gas constant (= 8.314 J/mol K)
  • T: Absolute temperature (K)

• Empirically varified over a large temperature range

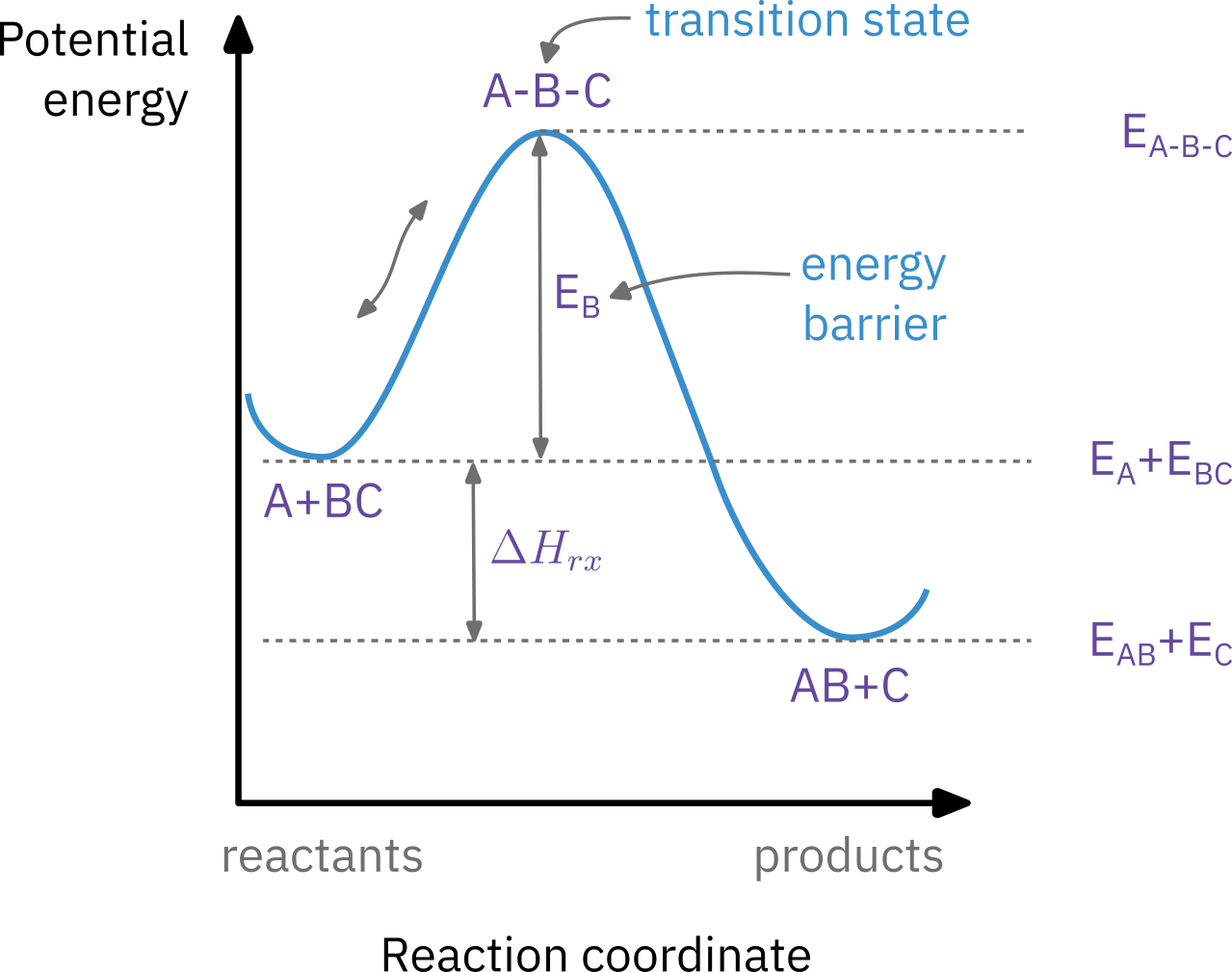
Activation energy

• Barrier to energy transfer (from kinetic energy to potential energy) between reacting molecules that must must be overcome.

• Minimum increase in potential energy of the reactants that must be provided to transform the reactants into products

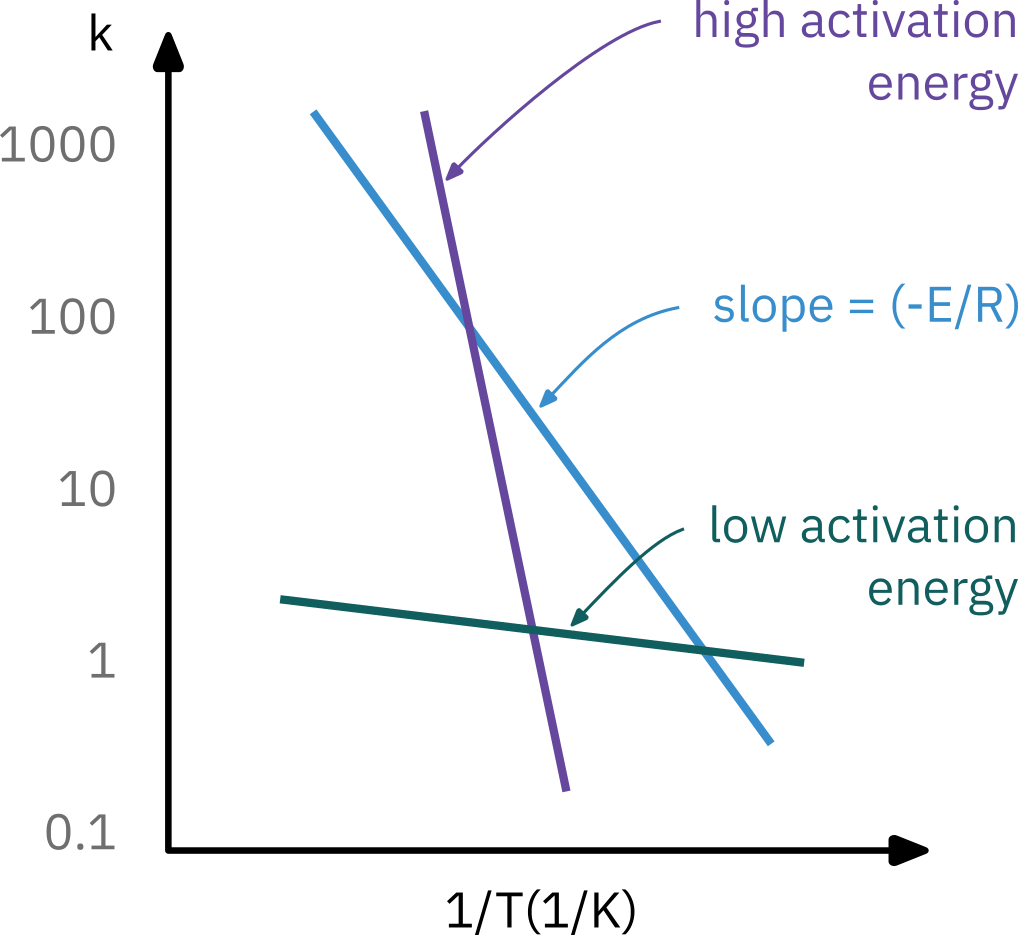
Determining activation energy

• Experimentally measuring reaction rate at different temperatures

• k_A(T) = A e^{-E/RT}

  Taking natural log

  \ln k_A = \ln A -\frac{E}{R} \left( \frac{1}{T} \right)

k(T) = k(T_0) e^{\frac{E}{R} \left( \frac{1}{T_0} - \frac{1}{T} \right)}

• Rule of thumb: Reaction rate doubles every 10 °C rise in temperature

Arrhenius plot

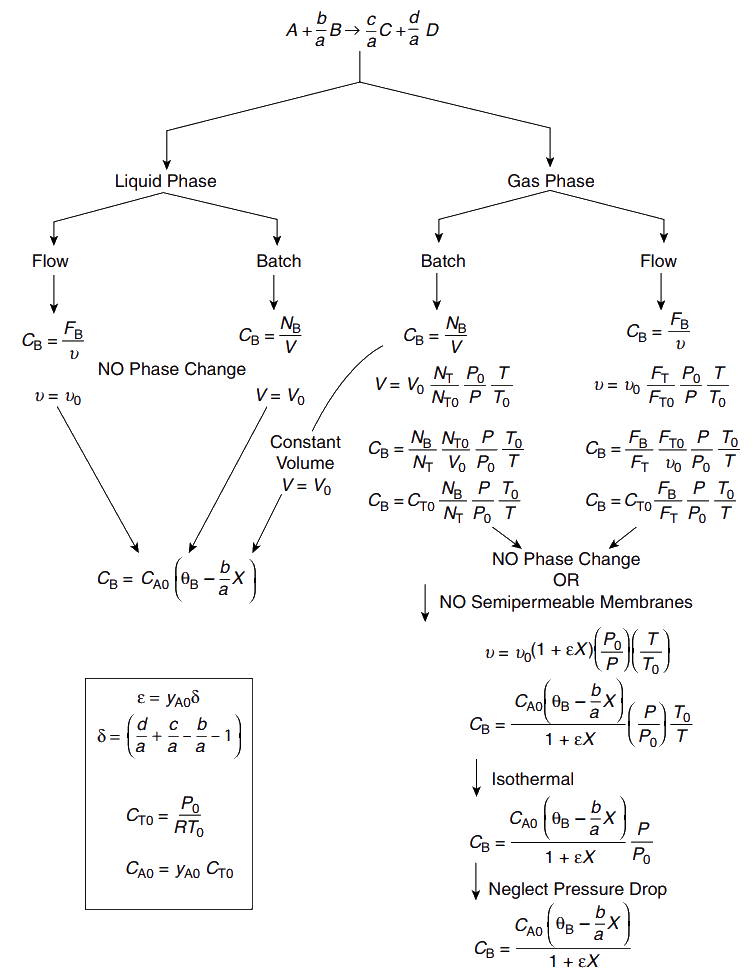
Stoichiometry

If the rate law depends on more than ne species, we must relate concentrations of different species to each other.

Stoichiometric table

• Represents stoichiometric relationships between reacting molecules for a single reaction

• How many molecules of one species will be formed during a chemical reaction given a number of molecules of another species disappear.

• Let us consider general reaction

  \ce{aA +bB -> cC + dD}

• relative rates

  \frac{-r_A}{a} = \frac{-r_B}{b} = \frac{r_C}{c} = \frac{-r_D}{d}

• Basis of calculation: Species A

  \ce{A +\frac{b}{a}B -> \frac{c}{a}C + \frac{d}{a}D}

Batch systems

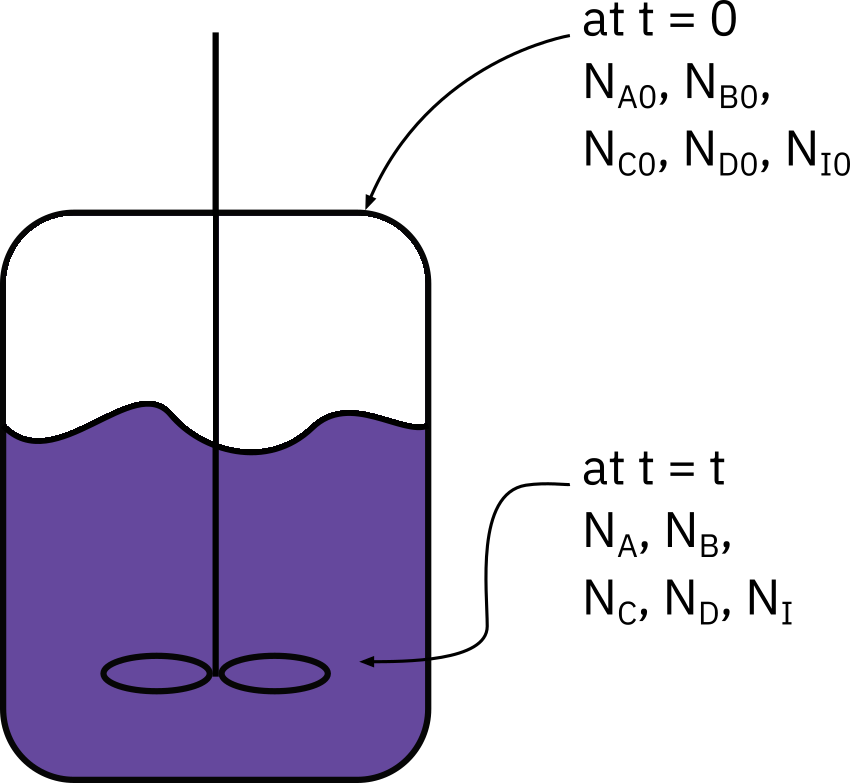
• Mole balance

  \frac{dN_A}{dt}=r_A V

• N_{A0} : No. of moles of A initially present

• X : Conversion at time t

• N_{A0}X : No. of moles of A consumed at time t

• N_{A} : No. of moles of A in system at time t

• N_{A} = N_{A0}-N_{A0}X = N_{A0}(1-X)

Stoichiometric table: batch systems

• Moles of B reacted

  moles\ of\ B\ reacted = \frac{mol\ B\ reacted}{mol\ A\ reacted} \times mol\ A\ reacted = \frac{b}{a} N_{A0} X

  Species	Initially (mol)	Change (mol)	Remaining (mol)
  A	N_{A0}	-N_{A0}X	N_A = N_{A0} - N_{A0}X
  B	N_{B0}	-(b/a)N_{A0}X	N_B = N_{B0} -(b/a)N_{A0}X
  C	N_{C0}	(c/a)N_{A0}X	N_C = N_{C0} +(c/a)N_{A0}X
  D	N_{D0}	(d/a)N_{A0}X	N_D = N_{D0} +(d/a)N_{A0}X
  I	N_{I0}	0	N_I = N_{I0}
  Total	\mathbf{N_{T0}}		\mathbf{N_T = N_{T0} + \delta N_{A0}X}

• \delta = +\frac{d}{a}+\frac{c}{a}-\frac{b}{a}-1

  Change in total number of moles per mole A reacted

Equations for the concentration

• C_A = \frac{N_A}{V} = \frac{N_{A0}(1-X)}{V}

• C_B = \frac{N_B}{V} = \frac{N_{B0}-(b/a)N_{A0}X}{V}

• C_C = \frac{N_C}{V} = \frac{N_{C0}+(c/a)N_{A0}X}{V}

• C_D = \frac{N_D}{V} = \frac{N_{D0}+(d/a)N_{A0}X}{V}

• For a constant volume batch reactor, V = V_0.

• Let \Theta_i= N_{i0}/N_{A0} = C_{i0}/C_{A0}.

• C_A = C_{A0}(1-X)
• C_B = C_{A0}(\Theta_B-(b/a)X)
• C_C = C_{A0}(\Theta_C+(c/a)X)
• C_D = C_{A0}(\Theta_D+(d/a)X)

\Theta_i= \frac{\text{Moles of species 'i' initially}}{\text{Moles of species A initially}}

Equimolar: \Theta_B = 1

Stoichiometric: \Theta_B = b/a

Rate expression

• -r_A = k C_A C_B

• -r_A = k C_{A0}^2 (1-X) (\phi_B-(b/a)X)

• For C_{A0}= C_{B0}, and b/a = 1

  -r_A = k C_{A0}^2 (1-X)^2

• Mole balance

  \frac{dC_A}{dt}=-k C_{A0}^2 (1-X)^2

  as C_A = C_{A0}(1-X); dC_A = -C_{A0} dX

• The mole balance can then be written as

  \frac{dX}{(1-X)^2}=k C_{A0} dt

Flow systems

• Form of stoichiometric table is virtually identical to batch systems

• Replace N_{j0} by F_{j0}

• Replace N_{j} by F_{j}

Stoichiometric table: flow systems

Species	Feed rate to reactor (mol/time)	Change within reactor (mol/time)	Effluent rate from reactor (mol/time)
A	F_{A0}	-F_{A0}X	F_A = F_{A0} - F_{A0}X
B	F_{B0}	-(b/a)F_{A0}X	F_B = F_{B0} -(b/a)F_{A0}X
C	F_{C0}	(c/a)F_{A0}X	F_C = F_{C0} +(c/a)F_{A0}X
D	F_{D0}	(d/a)F_{A0}X	F_D = F_{D0} +(d/a)F_{A0}X
I	F_{I0}	0	F_I = F_{I0}
Total	\mathbf{F_{T0}}		\mathbf{F_T = F_{T0} + \delta F_{A0}X}

• \delta = +\frac{d}{a}+\frac{c}{a}-\frac{b}{a}-1

• \Theta_{i0}= F_{i0}/F_{A0} = C_{i0}/C_{A0}.

• C_B = C_{A0}(\Theta_B-(b/a)X)

  For liquid phase systems (\upsilon = \upsilon_0)

Gas phase reactions

• Volumetric flow rate changes during the course of reaction

  • Changes in total number of moles

  • Changes in pressure and temperature

• Variable flow rate

  Gas phase reactions that do not have equal number of product and reactant moles

  e.g. \ce{N2 + 3H2 <=> 2NH3}

  • 4 mole reactant give 2 mole products

• Stoichiometric tables

  • No assumptions made reagarding volume

  • The tables are exactly same for constant volume (constant density) and variable volume (variable density) systems

\Rightarrow Only for concentration expressed in terms of conversion density/ volume comes into play.

Flow reactor with variable volumetric flow rate

• We will use relationships for total concentration

  C_T = \frac{F_T}{\upsilon} \qquad ... \qquad \frac{\text{total molar flow rate}}{\text{volumetric flow rate}}

• For gases

  C_T = \frac{P}{zRT} \qquad z: \text{compressibility factor (=1 for ideal gas)}

• At the entrance of the reactor

  C_{T0} = \frac{P_0}{z_0RT_0}

• Assuming negligible change in z (z = z_0)

  \upsilon = \upsilon_0 \left( \frac{F_T}{F_{T_0}} \right) \left( \frac{P_0}{P} \right) \left( \frac{T}{T_0} \right)

Flow reactor with variable volumetric flow rate

• We can now express C_j (=F_j/\upsilon) in terms of F, P, and T

  C_j = C_{T0} \left( \frac{F_j}{F_T} \right) \left( \frac{P}{P_0} \right) \left( \frac{T_0}{T} \right)

• F_T = \sum_{j=1}^{n} F_j = F_A + F_B + F_C + F_D + F_I

  F_j is found by solving mole balance equations

• Concentration in terms of conversion: F_T = F_{T0} + F_{A0} \delta X

• Dividing by F_{T0} and defining \epsilon = y_{A0} \delta, where y_{A0} is the mole fraction of A at inlet

  \frac{F_T}{F_{T0}} = 1 + \epsilon X

\epsilon = \frac{ \text{change in total no. of moles for complete conversion}} { \text{total moles fed}}

Flow reactor with variable volumetric flow rate

• Equation for volumetric flow rate \upsilon = \upsilon_0 (1 + \epsilon X) \left( \frac{P_0}{P} \right) \left( \frac{T}{T_0} \right)

• Molar flow rate F_j = F_{A0} (\Theta_j + \nu_j X)

• Concentration (C_j = F_j /\upsilon)

  C_j = \frac{F_{A0} (\Theta_j + \nu_j X)} {\upsilon_0 (1 + \epsilon X) \left( \frac{P_0}{P} \right) \left( \frac{T}{T_0} \right) }

• Stoichiometric coefficient (\nu_j)

\ce{ A + \frac{b}{a} B -> \frac{c}{a} C + \frac{d}{a} D}

• -ve for reactant

  \nu_A = -1; \nu_B = -b/a

• +ve for products

  \nu_C = c/a; \nu_D = -d/a

C_j = \frac{C_{A0} (\Theta_j + \nu_j X)} {(1 + \epsilon X)} \left( \frac{P}{P_0} \right) \left( \frac{T_0}{T} \right)

Summary

Fogler, H. Scott. 2016. Elements of Chemical Reaction Engineering. Fifth edition