| X | 0.00 | 0.10 | 0.20 | 0.40 | 0.60 | 0.70 | 0.80 |
| 0.89 | 1.08 | 1.33 | 2.05 | 3.56 | 5.06 | 8.00 |
Conversion and reactor sizing
Chemical Reaction Engineering
Is this a reactor













Review - general mole balance
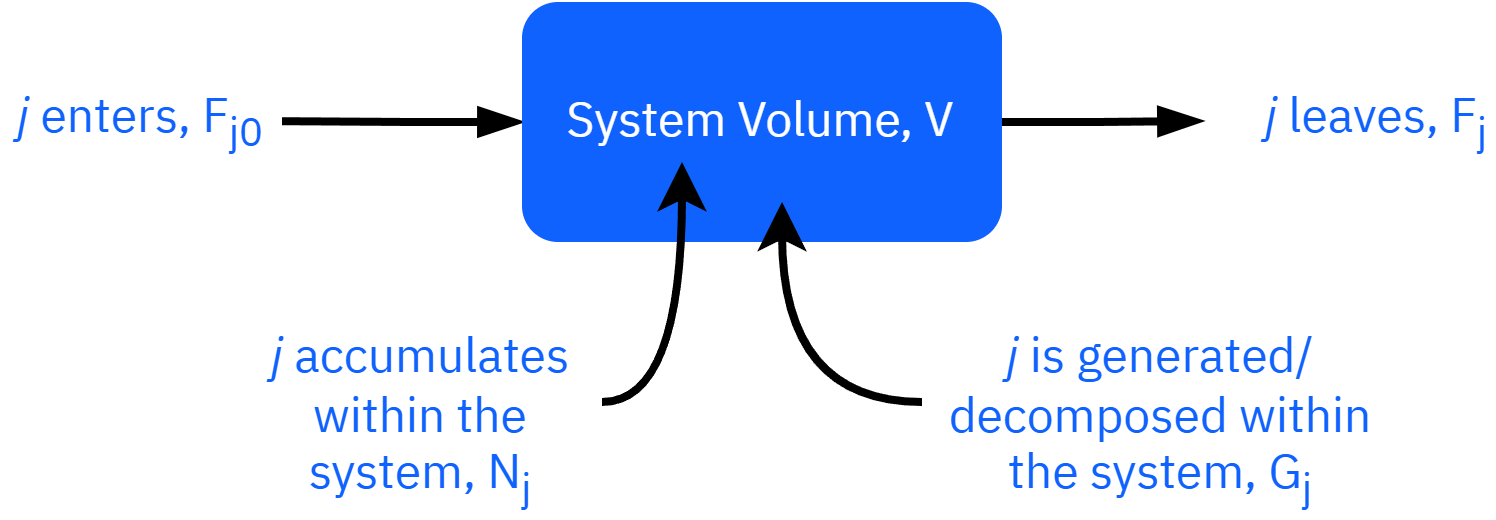
General form: Fj0−Fj+Gj=dtdNj
Uniform generation Fj0−Fj+rjV=dtdNj
Non-uniform generation Fj0−Fj+∫VrjdV=dtdNj
Reactor mole balance
| Reactor | Differential form | Algebraic form | Integral form |
|---|---|---|---|
| Batch | dtdNA=rAV | t=∫NA0NArAVdNA | |
| CSTR | V=−rAFA0−FA | ||
| PFR | dVdFA=rA | V=∫FA0FArAdFA | |
| PBR | dWdFA=rA′ | W=∫FA0FArA′dNA |
Conversion, X
Conversion is convenient for relating: rj,V,υ,Nj,Fj,and Cj
Consider the generic reaction
aA+bBcC+dD
Choose limiting reactant A as basis of calculation and normalize
A+ab Bac C+ad D
Conversion (X): The fraction or percentage of a reactant that is consumed during a chemical reaction.
X=moles of A fedmoles of A reacted
Batch system: “Moles A fed” is the amount of A at the start of the reactor (t=0) Flow system: “Moles A fed” is the amount of A entering the reactor
Conversion, X
Consider A+2B2C, Start with 1 mole of A, and 1 mole of B
A is the basis:
At the end we have
1 mole A, 1 mole B
XA=0/1=0 ⇒no reaction
21 mole A, 0 mole B
XA=0.5/1=1/2(0.5)
0 mole A, -1 mole B
XA=1/1=1 ⇒complete reaction, but not possible
B is the basis:
At the end we have
1 mole A, 1 mole B
XB=0/1=0 ⇒no reaction
21 mole A, 0 mole B
XB=1/1=1 ⇒complete reaction
Pick the limiting reagent as the basis to calculate conversion
Moles and molar flow rate in terms of XA
A+ab Bac C+ad DX=moles of A fedmoles of A reacted
Batch systems: Longer reactant is in reactor, more reactant is converted to product (until reactant is consumed or the reaction reaches equilibrium)
NA=NA0−NA0XA
NA=NA0(1−XA)
Flow systems: For a given flow rate, the larger the reactor, the more time it takes the reactant to pass through the reactor, the more time to react
FA=FA0−FA0XA
FA=FA0(1−XA)
Design equation in terms of X: Batch reactor
Ideal batch reactor design equation
dtdNA=rAV
NA=NA0(1−XA)
Taking the derivative of NA equation
dtdNA=dtd(NA0(1−XA))
dtdNA=0−NA0dtdXA
Substituting
NA0dtdXA=−rAV
t=NA0∫0XA−rAVdXA
In class exercise
Derive Design equation for a CSTR in terms of X.
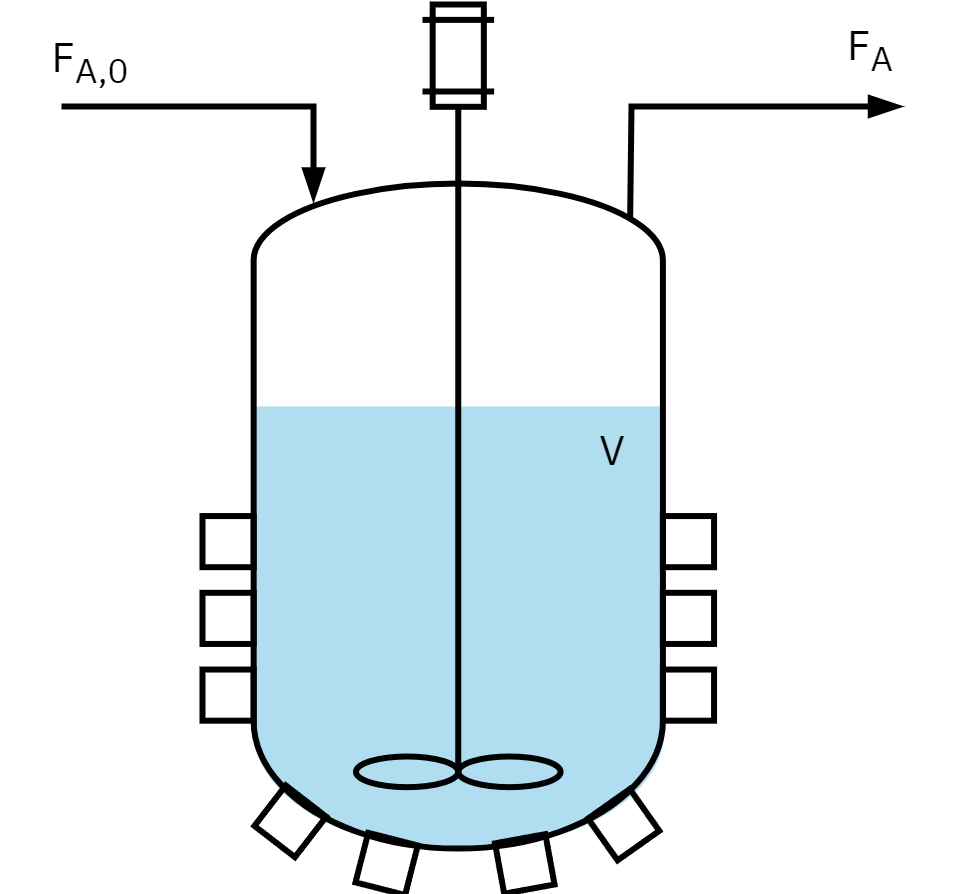
Design equation in terms of X: CSTR
Ideal steady state CSTR design equation
V=−rAFA0−FA
Substitute for FA
FA=FA0(1−XA)
V=−rAFA0−[FA0−FA0XA]
V=−rAFA0XA

V is the CSTR volume required to achieve a specified conversion. XA and –rA are evaluated at the exit of the CSTR
In class exercise
Derive Design equation for a PFR in terms of X.

Design equation in terms of X: PFR
Ideal steady state PFR design equation
dVdFA=rA
FA=FA0(1−XA)
Taking the derivative of FA equation
dVdFA=dVd(FA0(1−XA))
dVdFA=0−FA0dVdXA⇒dVdFA=−FA0dVdXA
Substituting
FA0dVdXA=−rA⇒V=FA0∫0XA−rAdXA
Design equation in terms of X: PBR

Ideal steady state PBR design equation
dWdFA=rA′
FA=FA0(1−XA)
Taking the derivative of FA equation
dWdFA=dWd(FA0(1−XA))
dWdFA=−FA0dWdXA
Substituting
FA0dWdXA=−rA′⇒W=FA0∫0XA−rA′dXA
::::
Reactor mole balance in terms of X
| Reactor | Differential form | Algebraic form | Integral form |
|---|---|---|---|
| Batch | NA0dtdX=rAV | t=NA0∫0XrAVdX | |
| CSTR | V=−rAFA0X | ||
| PFR | FA0dVdX=−rA | V=FA0∫0X−rAdX | |
| PBR | FA0dWdX=−rA′ | W=FA0∫0X−rA′dX | |
Sizing of continuous flow reactors
Sizing refers to either of
- Determining reactor volume for specified conversion
- Determining conversion for a specified volume
For All irreversible reactions of order greater than 0, As we approach complete conversion, the reciprocal rate approaches infinity
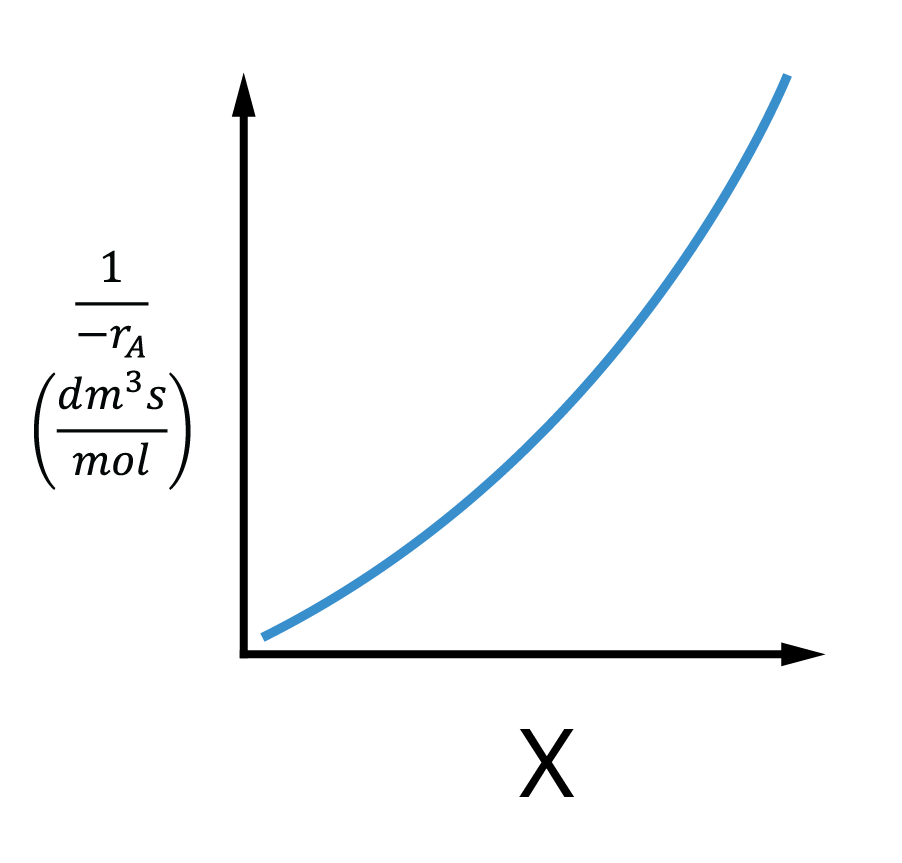
Irreversible reaction:
As X→1;−rA→0
Reversible reaction:
As X→Xe;−rA→0
⇒−rA1→∞∴V→∞
Infinite reactor volume is necessary to reach complete conversion
Sizing of continuous flow reactors
CSTR
V=((−rA)exitFA0)⋅X
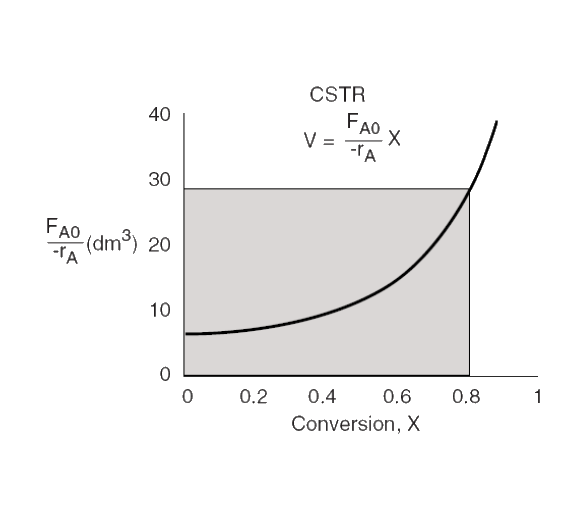
CSTR volume
area of rectangle bound by XA and −rA,exitFA0
PFR
V=∫0X((−rA)FA0)dX
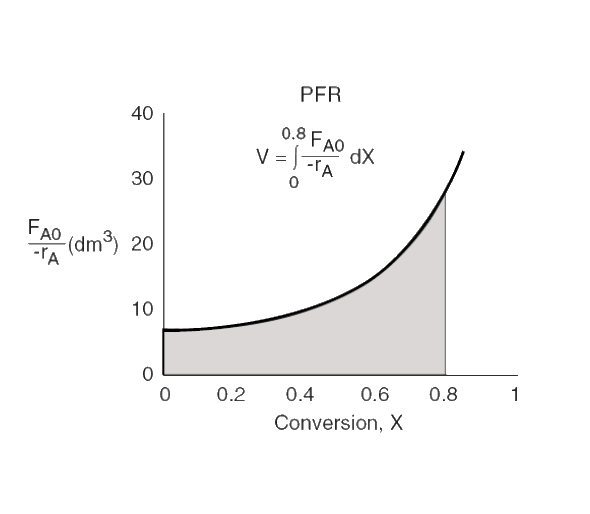
PFR volume
area under the curve −rAFA0=f(XA)
Levenspiel plots - reactor sizing
Given –rA as a function of conversion, −rA=f(X), one can size any type of reactor.
We do this by constructing a Levenspiel plot.
Here we plot either −rAFA0 or −rA1 as a function of X.
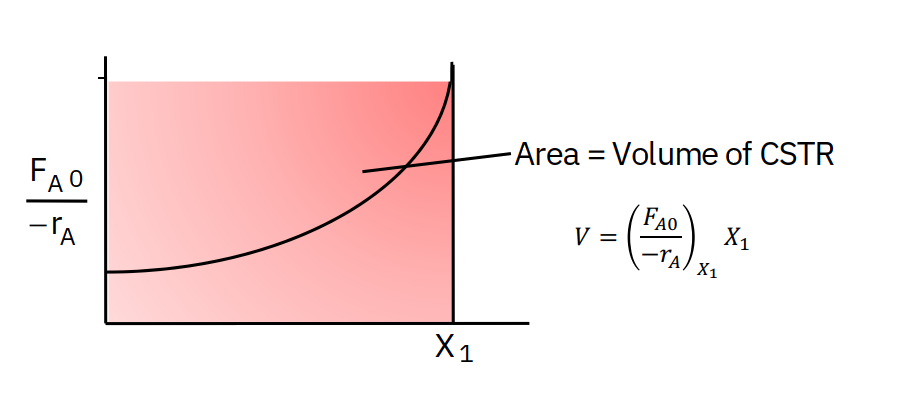

In class exercise: CSTR sizing
Using following data: Calculate VCSTR for X=0.4, and X=0.8
CSTR sizing
Using following data: Calculate VCSTR for X=0.4, and X=0.8
| X | 0.00 | 0.10 | 0.20 | 0.40 | 0.60 | 0.70 | 0.80 |
| −rAFA0 | 0.89 | 1.08 | 1.33 | 2.05 | 3.56 | 5.06 | 8.00 |

V=((−rA)exitFA0)⋅X
For X = 0.4; (−rA)exitFA0 = 2.05 m3
V = 0.82 m3
For X = 0.8; (−rA)exitFA0 = 8.00 m3
V = 6.4 m3
In class exercise: PFR sizing
Using following data: Calculate VPFR for X=0.4, and X=0.8
| X | 0.00 | 0.10 | 0.20 | 0.40 | 0.60 | 0.70 | 0.80 |
| −rAFA0 | 0.89 | 1.08 | 1.33 | 2.05 | 3.56 | 5.06 | 8.00 |
PFR sizing
Using following data: Calculate VPFR for X=0.4, and X=0.8
| X | 0.00 | 0.10 | 0.20 | 0.40 | 0.60 | 0.70 | 0.80 |
| −rAFA0 | 0.89 | 1.08 | 1.33 | 2.05 | 3.56 | 5.06 | 8.00 |

V=∫0X((−rA)FA0)dX
For X = 0.4; Numerically integrate the data
V = 0.55 m3
For X = 0.8; (−rA)exitFA0 = 8.00 m3
V = 2.15 m3
Reactors in series
Reactors are arranged sequentially, with the output of one reactor feeding directly into the next.
Advantages:
- Achieve higher overall conversion rates
- Handle reactions requiring different conditions at different stages.
- Different reaction conditions can be optimized in each reactor.
- Staging: Allows for the introduction of intermediates or the removal of by-products between stages.
Both Continuous Stirred Tank Reactors (CSTRs) and Plug Flow Reactors (PFRs) can be configured in series, either separately or in a mixed arrangement, to optimize reaction conditions and efficiencies.
Key Considerations
- Reactor volume and design optimization
- Maintenance and operational complexity
Levenspiel plots can be used to visualize and sequence reactors in series.
Reactors in series

In absence of any side streams (inlets or outlets)
Conversion up to point i:
Xi=Moles A fed into 1st reactortotal moles of A reacted up to point i
Molar Flow rate of species A at point i:
FAi=FA0−FA0Xi
Reactors in series
Example: An adiabatic liquid-phase isomerization
The isomerization of butane
n-CX4HX10i-CX4HX10
was carried out adiabatically in the liquid phase. The data for this reversible reaction are given below. Calculate the volume of each of the reactors for an entering molar flow rate of n-butane of 50 kmol/hr.
| X | 0.00 | 0.20 | 0.40 | 0.60 | 0.65 |
| −rA,m3⋅hkmol | 39.00 | 53.00 | 59.00 | 38.00 | 25.00 |
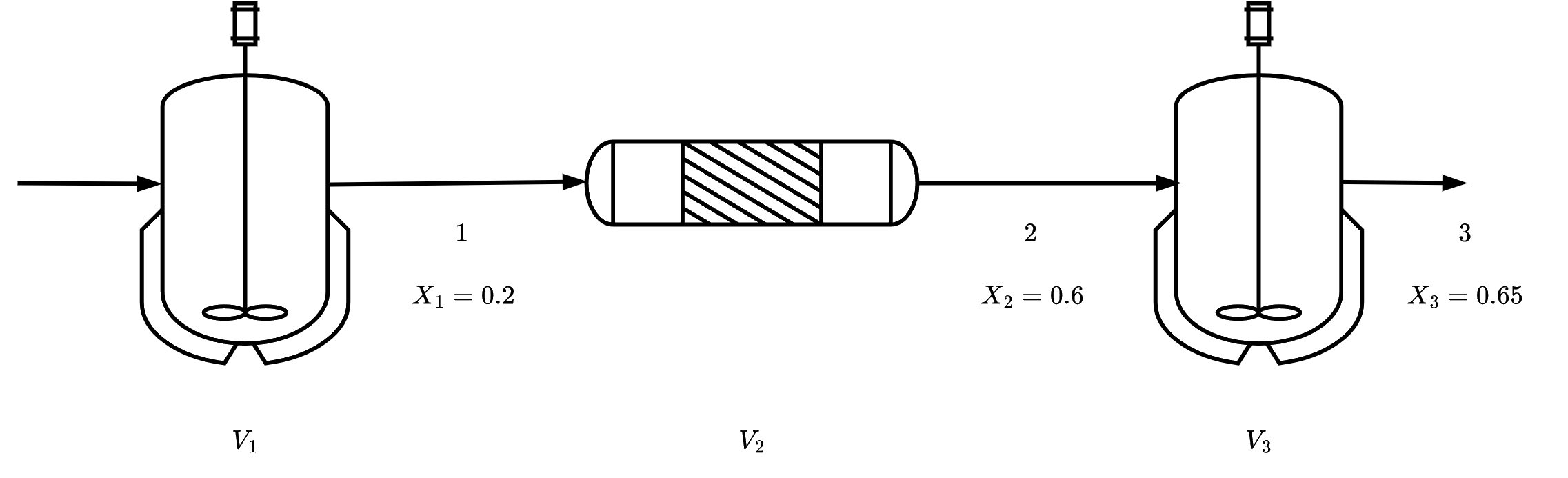
Reactors in series
Example: An adiabatic liquid-phase isomerization

Reactors in series
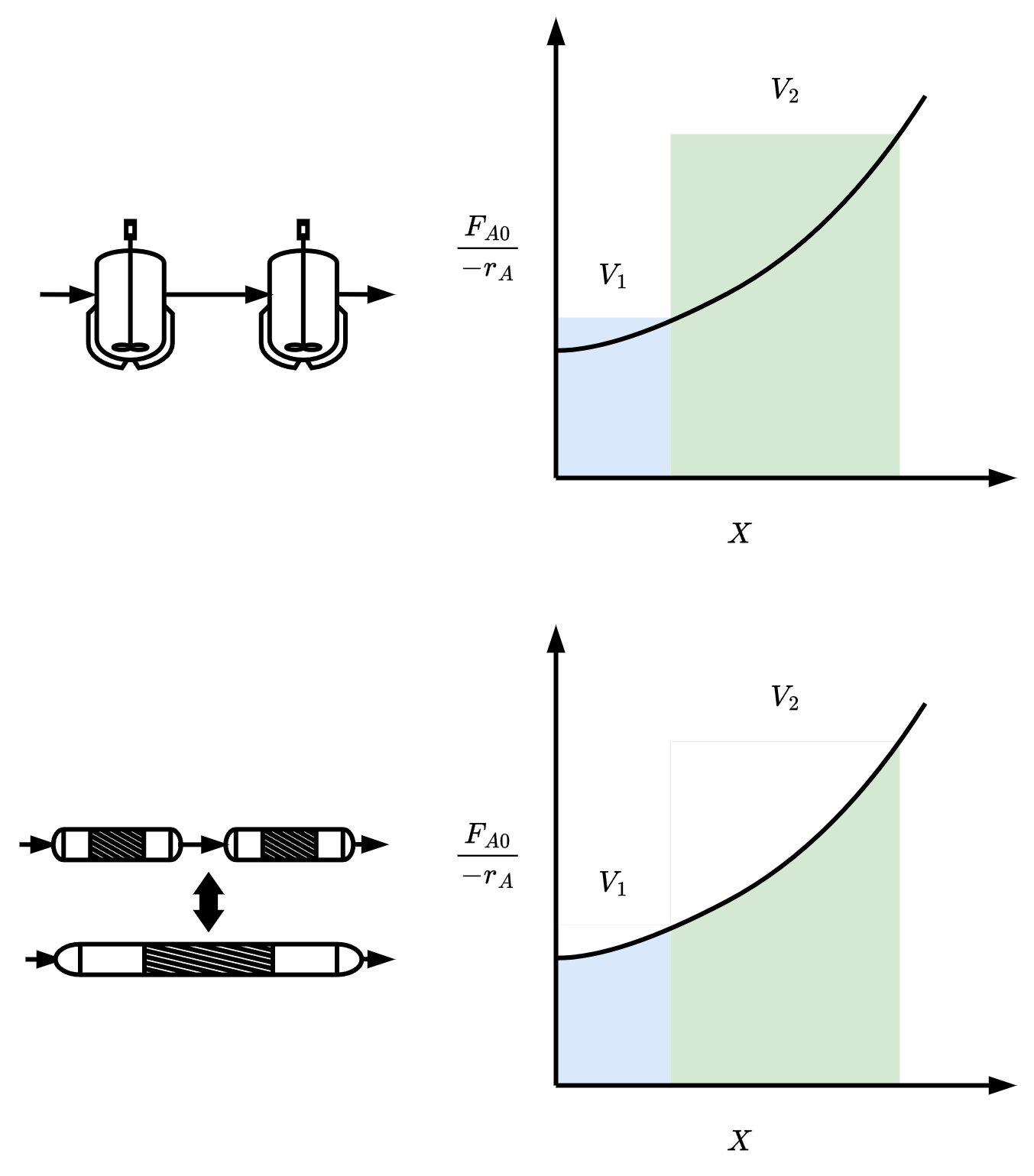
- If −rAFA0 monotonically increases with X
Vone PFR≤i∑VPFR(i)+j∑VCSTR(j)≤Vone CSTR
for any combination of PFRs and CSTRs in series
In general
1 PFR = any number of PFRs in series
1 PFR = ∞ number of CSTRs in series
For large number of CSTRs in series, the total volume is ‘roughly’ same as volume of PFR
The concept of using CSTRs in series to model PFR is used in larger number of situations such as modeling catalyst decay in packed bed reactors, or studying transient heat effects in PFR.
Space time (τ)
Time necessary to process one reactor volume, also called mean residence time or holding time
τ=υ0V
Space velocity (SV): inverse of space time, but vo may be measured under different conditions than the space time
SV=Vυ0=τ1
- LHSV: Liquid hourly space velocity: LHSV=Vυ0∣liquid
- GHSV: Gas hourly space velocity: GHSV=Vυ0∣STP
- υ0∣ is the volumetric flow rate measured at specified condition
This component is an instance of the CodeMirror interactive text editor. The editor has been configured so that the Tab key controls the indentation of code. To move focus away from the editor, press the Escape key, and then press the Tab key directly after it. Escape and then Shift-Tab can also be used to move focus backwards.

Chemical Reaction Engineering