Mole balances
Chemical Reaction Engineering
Introduction
- Chemical processes
- What is reaction engineering?
- Industrial reactors
- Overview of reaction engineering
Chemical processes


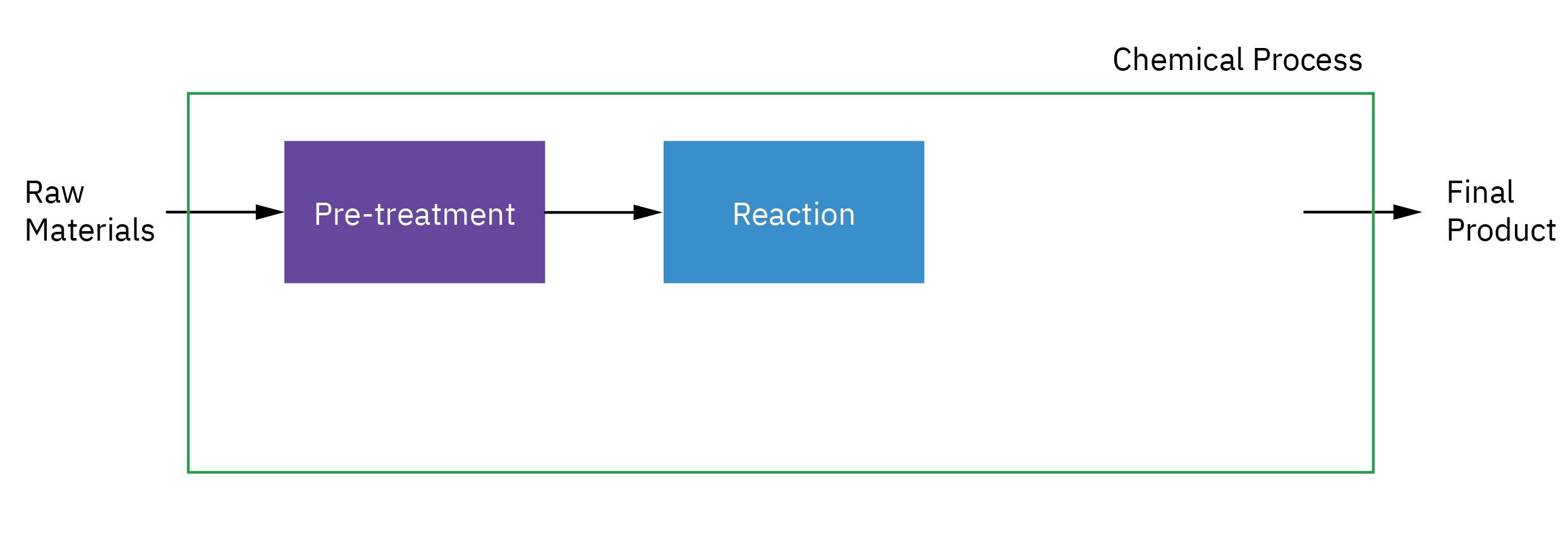
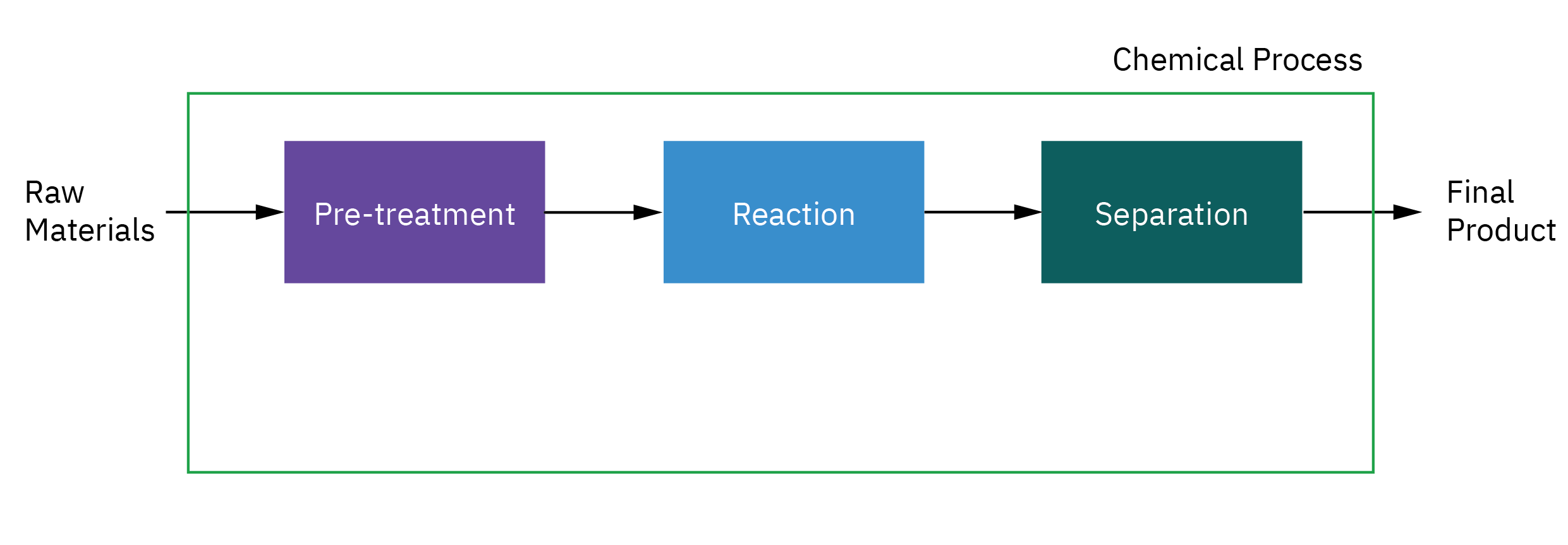

Selection of reactor system is key to economic success or failure of a chemical plant
Understanding how chemical reactors work lies at the heart of almost every chemical processing operation.
What is reaction engineering
CRE is the field that studies the rates and mechanisms of chemical reactions and the design of the reactors in which they take place.
Reactor design is a specialized task that involves evaluating various options. It draws on knowledge from thermodynamics, kinetics, fluid mechanics, and heat and mass transfer, along with economic considerations.
CRE is the synthesis of all these factors with the aim of properly designing and understanding the chemical reactor.

It is the primary knowledge of chemical kinetics and reactor design that distinguishes the chemical engineer from other engineers
Industrial reactors
Batch reactor

Industrial reactors
Tubular reactor

Industrial reactors
Stirred reactor

Industrial reactors
Catalytic cracking reactor

Industrial reactors
Calcination kiln

Industrial reactors
Microreactors

Industrial reactors
Electrolyzers

Industrial reactors
Raceway ponds

How do we design a chemical reactor?

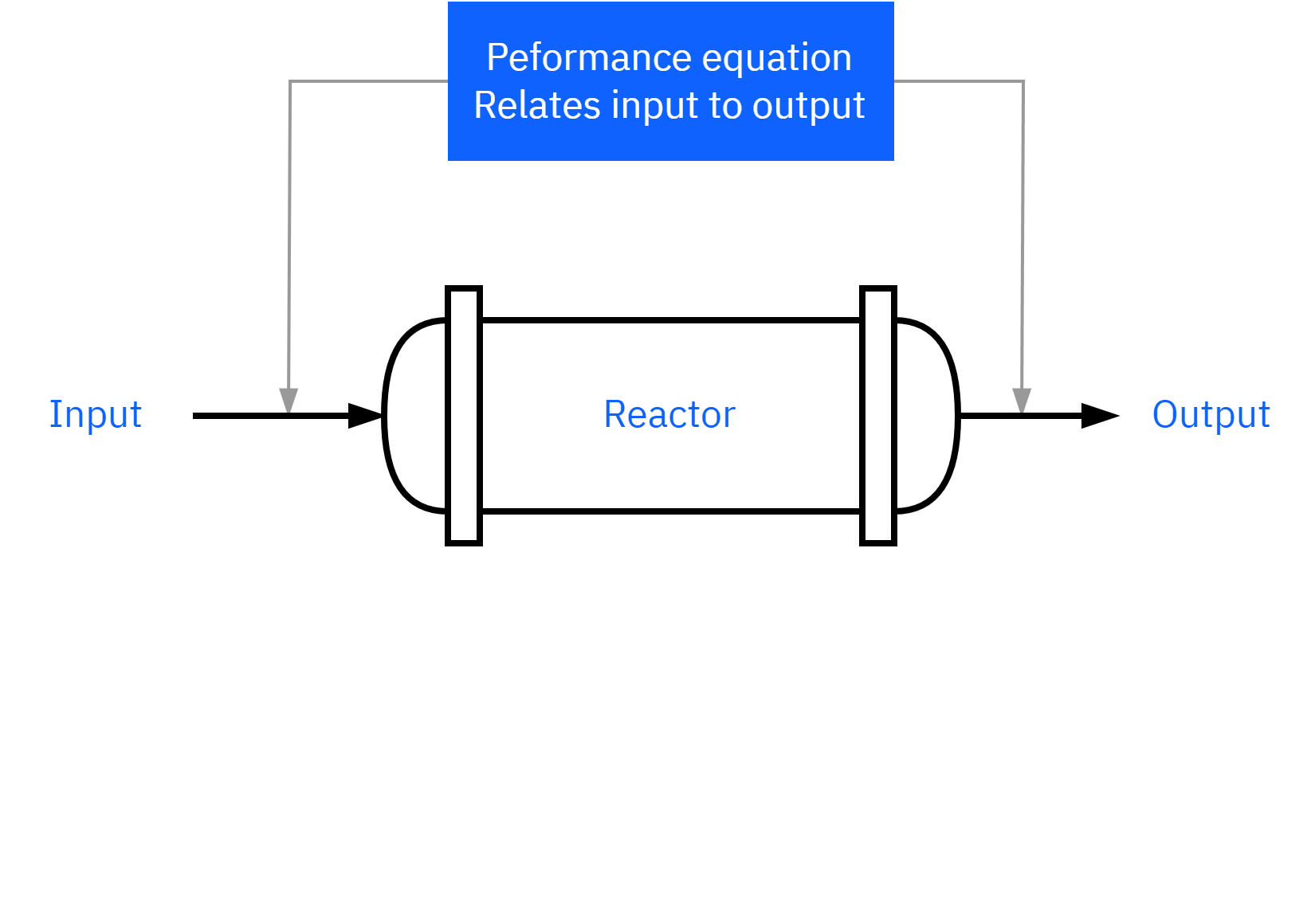
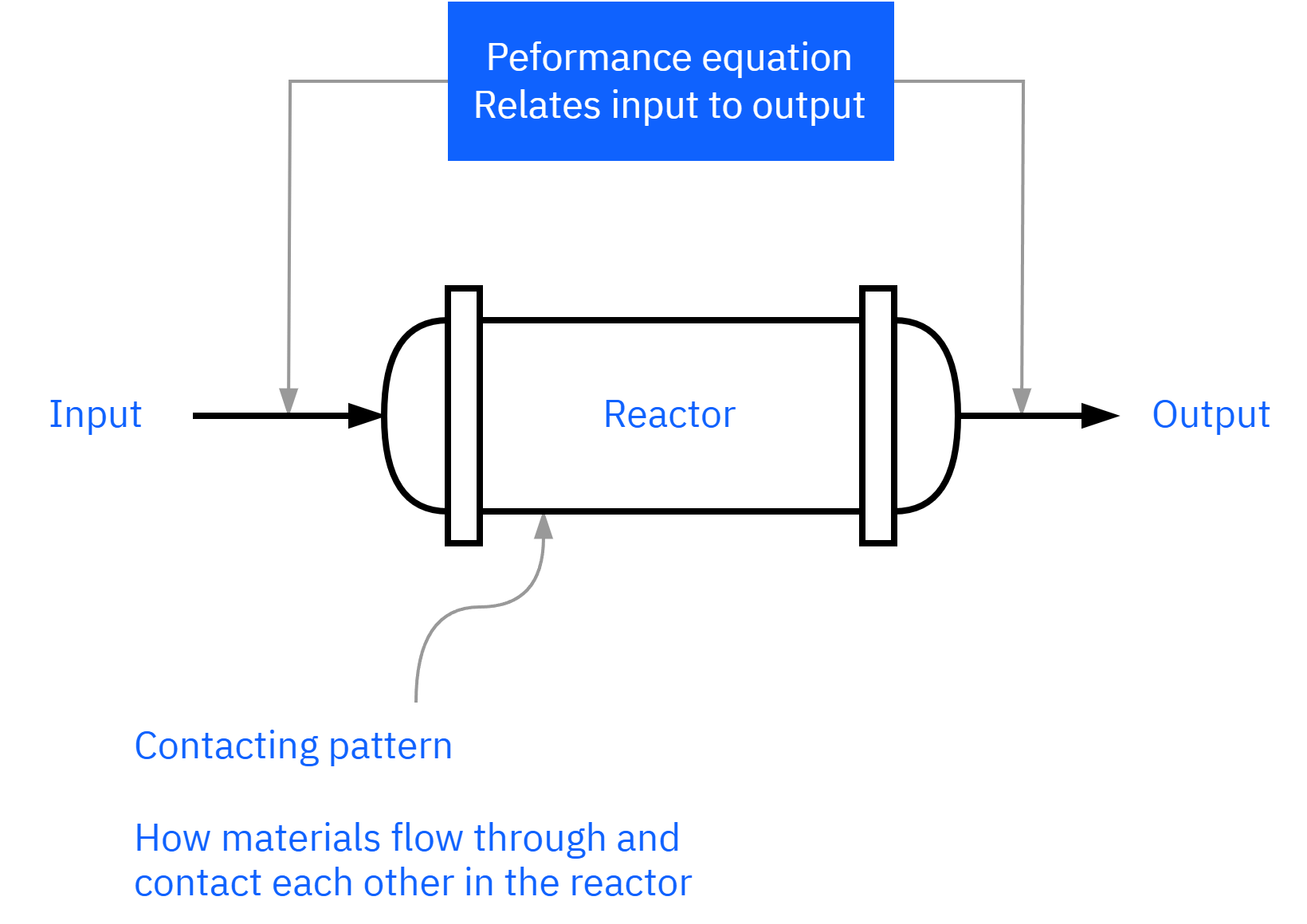
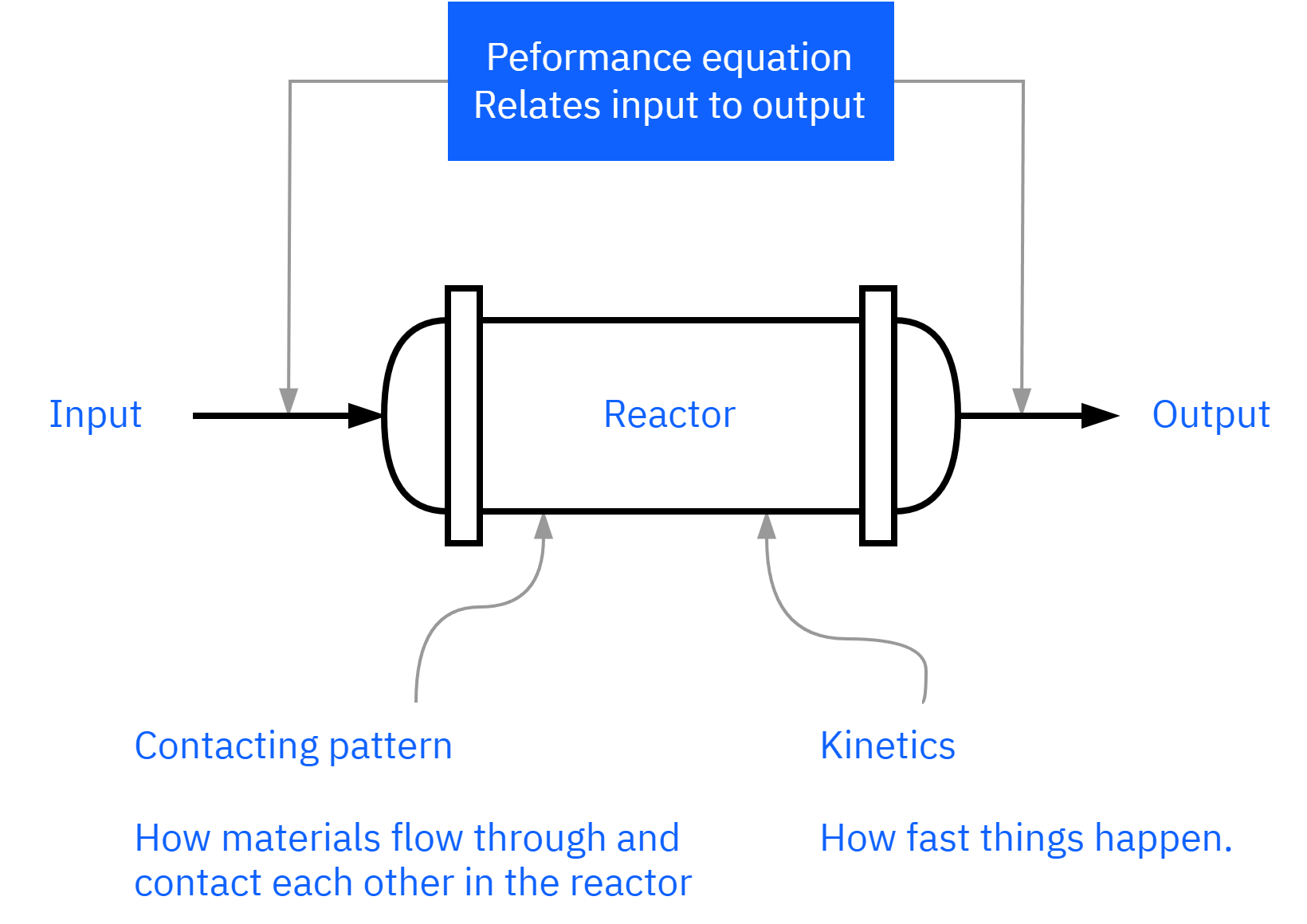
How do we design a chemical reactor?
Maximize the space-time yield

Reaction
- Stoichiometry
- Kinetics: elementary vs non-elementary
- Single vs multiple reactions
Reactor
- Isothermal vs non-isothermal
- Ideal vs nonideal
- Steady-state vs nonsteady-state
Mole balance
Rate of reaction
Basic mole balance
Mole balance in reactors
- Batch reactor
- Continuous stirred tank reactor (CSTR)
- Plug flow reactor (PFR)
- Packed bed reactor (PBR)
Reaction rate
A chemical species is said to have reacted when it has lost its chemical identity.
The identity of a chemical species is determined by the kind, number, and configuration of that species’ atoms.
There are three ways for a species to loose its identity:
Decomposition: CHX3−CHX3HX2+HX2C=CHX2
Combination: NX2+OX22NO
Isomerization: CX2HX5CH=CHX2CHX2=C(CHX3)X2
The rate of reaction tells us how fast a number of moles of one chemical species are being consumed to form another chemical species.
The rate of a reaction (mol/dm3/s) can be expressed as either:
- The rate of Disappearance of reactant: −rA
- The rate of Formation (Generation) of product: rP
Reaction rate
A+BC+D
- rA,rB = the rate of formation of species A, and B per unit volume
- −rA,−rB = the rate of a disappearance of species A, and B per unit volume
- rC,rD = the rate of formation of species C, and D per unit volume
- For species j:
- rj is the rate of formation of species j per unit volume [e.g. mol/dm3s]
- rj is a function of concentration, temperature, pressure, and the type of catalyst (if any)
- rj is independent of the type of reaction system (batch, plug flow, etc.)
- rj is an algebraic equation, not a differential equation
The algebraic expression for the reaction rate equation, rj, is also known as the rate law.
Rate law
−rA=f[temperature dependent terms,concentration dependent terms]
Some examples of rate law
Arrhenius equation: −rA=Ae−EA/RTCAa
- A: Pre-exponential factor
- EA: Activation energy
- R: Gas constant
- T: Temperature
- CA: concentration
- a: order of the reaction
Michaelis-Menton kinetics: −rA=1+k2CAk1CA
For a catalytic reaction we refer to –rA’ , which is the rate of disappearance of species A on a per mass of catalyst basis. (mol/gcat/s).
General mole balance
in−out+generation=accumulation
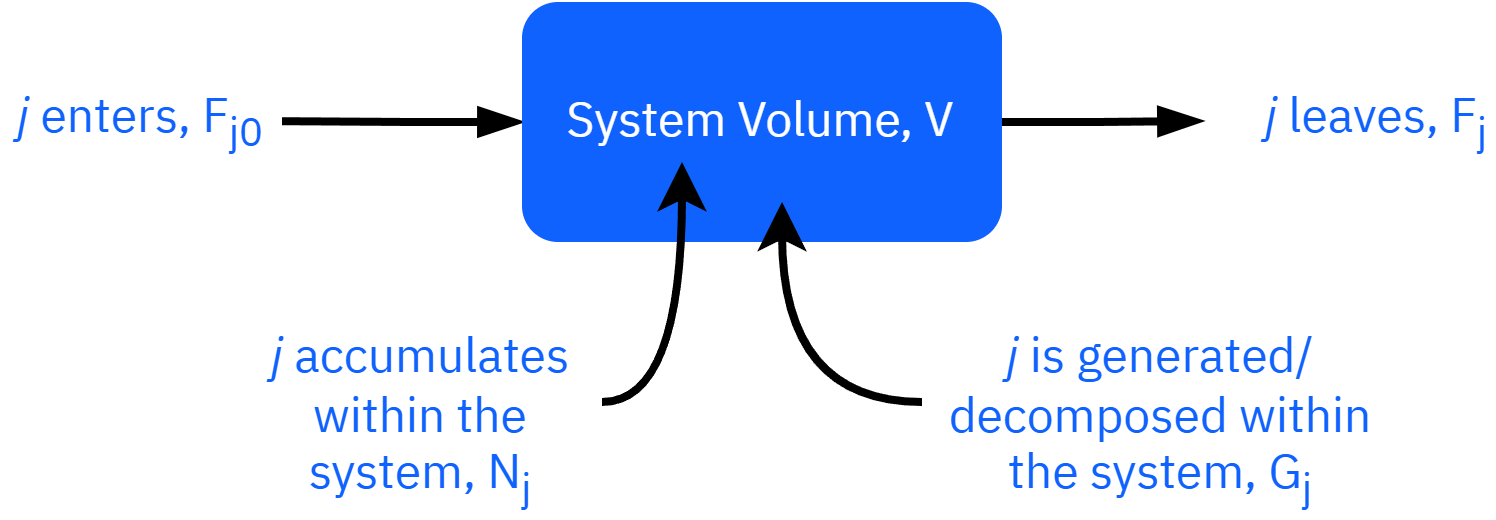
rate offlow of jinto system−rate offlow of jout of system+rate ofgenerationof j by rxn−rate ofdecompositionof j by rxn=rate ofaccumulationof j
Fj0−Fj+Gj=dtdNj
smol+smol+smol=dtd(mol)
Uniform generation
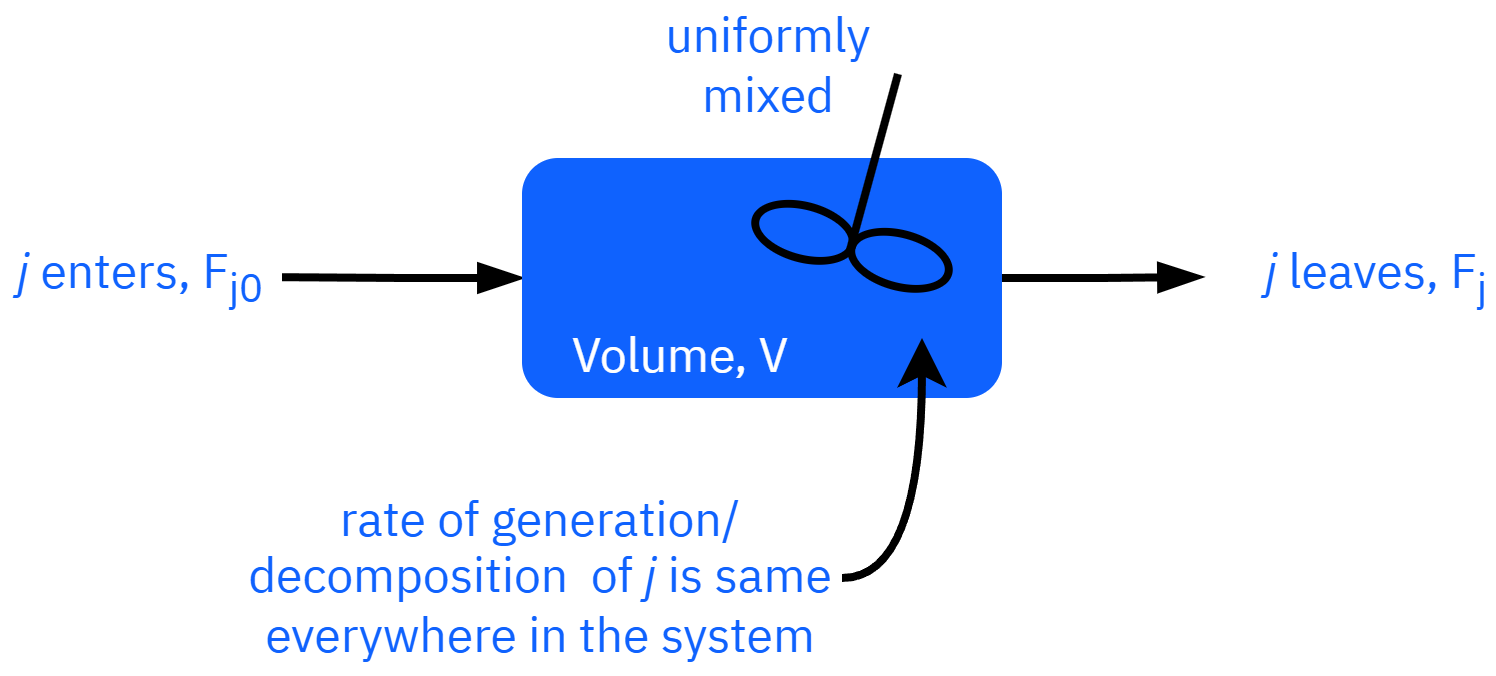
Gj=rjV
moles of jgenerated perunit time(mol/s)=moles of jgenerated perunit time andvolume (mol/s⋅m3)Volume(m3)
Fj0−Fj+rjV=dtdNj
Non-uniform generation
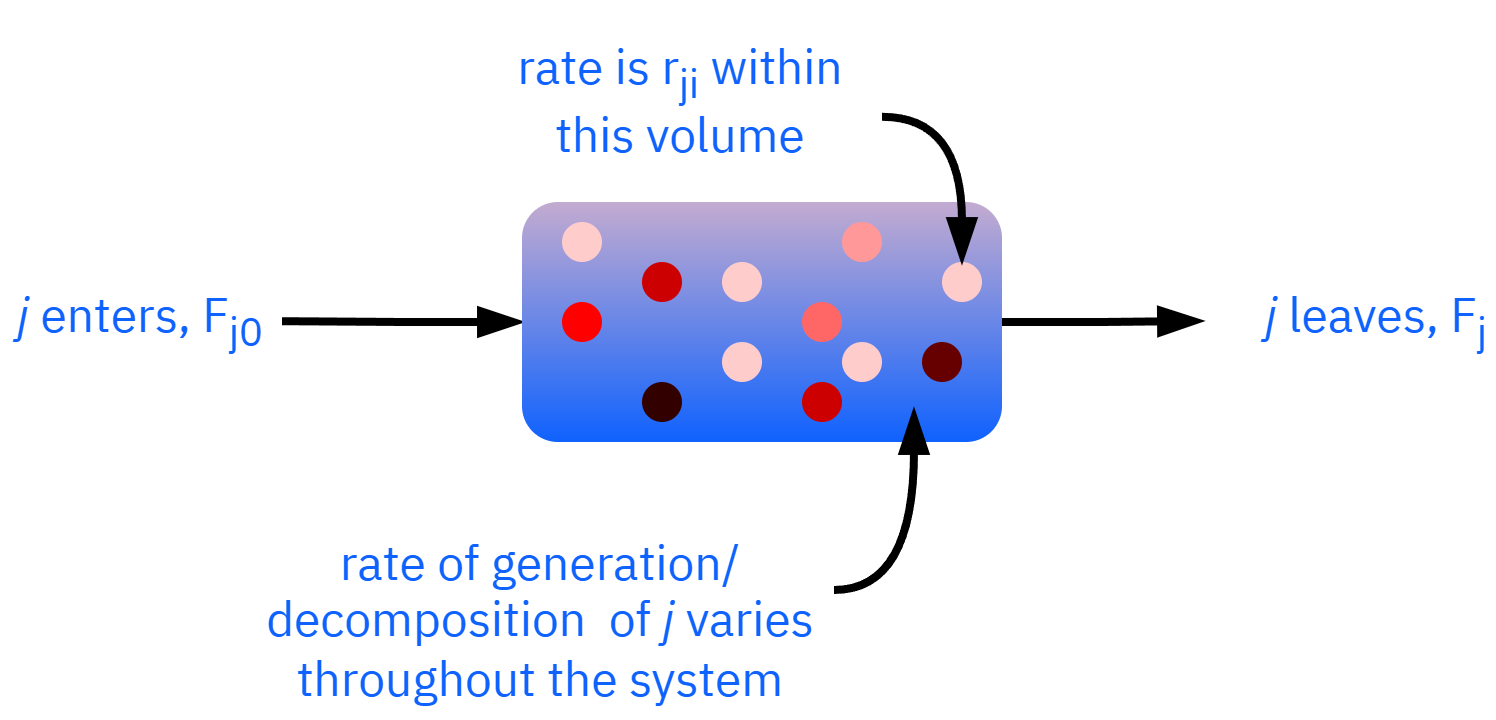
Gj=i=1∑nrjiΔVi
Gj=n→∞ΔV→0limi=1∑nrjΔV=∫VrjdV
Fj0−Fj+∫VrjdV=dtdNj
Review - general mole balance

General form: Fj0−Fj+Gj=dtdNj
Uniform generation Fj0−Fj+rjV=dtdNj
Non-uniform generation Fj0−Fj+∫VrjdV=dtdNj
Batch reactor
Reactants placed in reactor (Charge); reaction allowed to proceed over time.
Closed system: no reactants added or products removed during reaction.
Unsteady-state: composition changes over time.
Ideal batch reactor: contents perfectly mixed.
Concentration and temperature are uniform throughout the reactor but change with time.
Typical uses: Small scale operations, expensive products (e.g. pharmaceutical), new processes.

Mole balance: Batch reactor
Assumptions
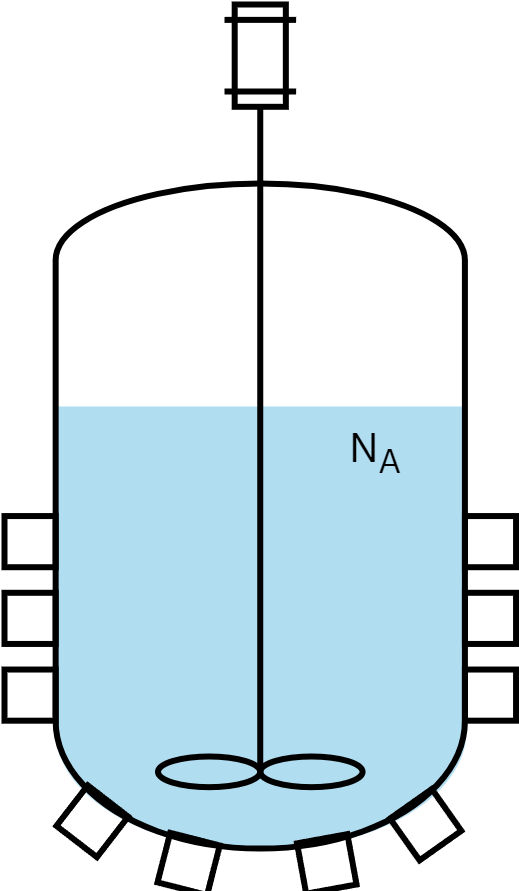
- Perfect mixing: The reactor contents are perfectly mixed (Ideal reactor).
- Constant Volume: The reactor volume is constant.
- Constant Physical Properties: The physical properties (density, viscosity, etc.) of the reaction mixture are constant.
- Single Reaction Phase: The reaction is assumed to occur in a single phase (either all gas, all liquid, or all solid).
- Closed system: No material is lost to the surroundings.
Mole balance: Batch reactor

Continuous stirred tank reactor (CSTR)

- Open system: Reactants are continuously fed and products removed.
- The incoming stream blends immediately with the reactor’s contents.
- Perfect mixing: similar to an ideal batch reactor.
- Temperature and concentration are consistent throughout.
- Exit stream composition matches the reactor’s interior.
- Reaction rates are constant, maintaining steady-state.
- Typical uses: Large-scale industrial chemical production (e.g. metallurgy), wastewater treatment
Mole balance: CSTR
Assumptions
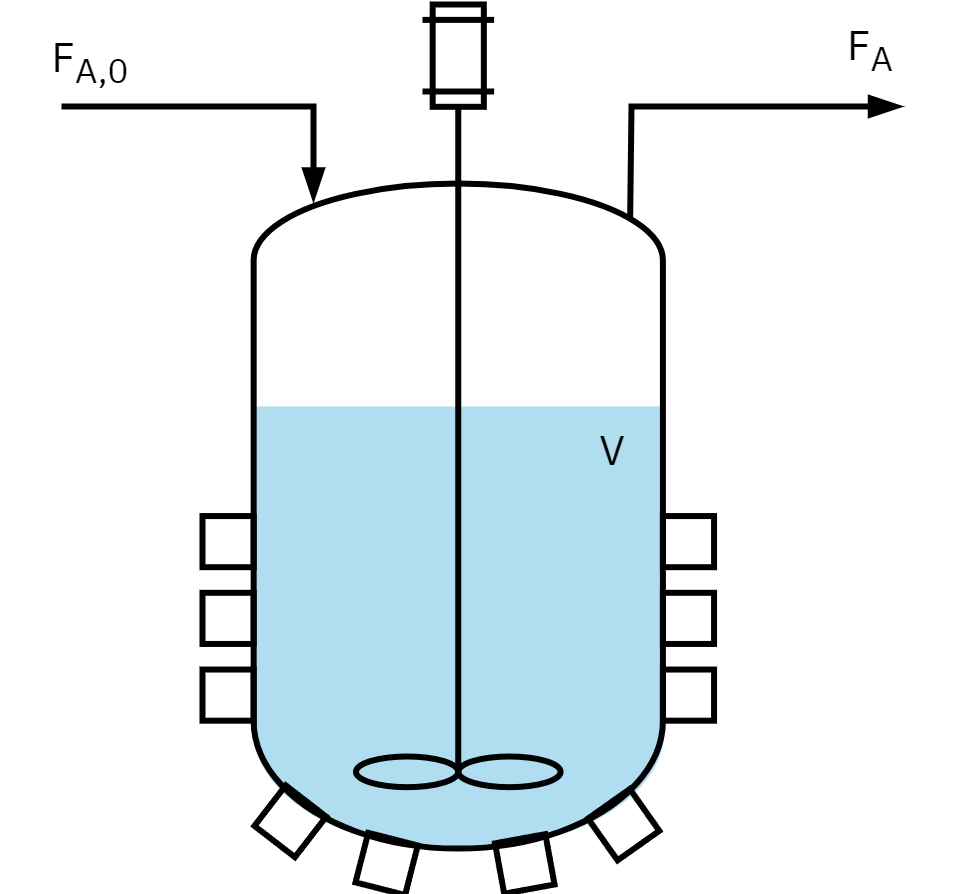
- Steady-State Operation: No accumulation of reactants or products over time.
- Continuous Flow: Material continuously flows into and out of the reactor.
- Perfect mixing: The composition is uniform throughout the reactor.
- Constant Volume: The volume of fluid within reactor remains constant.
- Constant Physical Properties
Mole balance: CSTR

Plug flow reactor (PFR)

- Also known as a tubular reactor.
- Cylindrical shape with openings at both ends.
- Materials move steadily through the reactor’s length.
- Reactants are consumed along the reactor’s length.
- Steady state operations:
- No radial gradients Temperature, concentration, reaction rates are constant at any given cross section.
- All material spends exactly same time in the reactor.
- Typical examples: Food industry (continuous baking or sterilization), polymerization reactions
Mole balance: PFR
Assumptions

- Steady-State Operation: no accumulation of materials in any section of the reactor over time.
- Plug Flow: The flow through the reactor is plug flow, meaning all elements of the fluid move with the same velocity and there’s no back-mixing.
- Constant Cross-Sectional Area: The cross-sectional area of the PFR is constant along its length.
- One-Dimensional Flow: The flow of reactants and products is considered only in the axial direction, ignoring effects in the radial or circumferential directions. Concentration and temperature changes along the length of the reactor not radially.
- No pressure drop; Constant Physical Properties
Mole balance: PFR

Packed bed reactor (PBR)
Vertical cylindrical shell design.
Flow is often gravity-driven.
Heterogeneous reactions with a fixed catalyst bed.
Reactants pass from top through the catalyst layer.
Concentration gradient forms along the reactor’s length.
Reactions occur at catalyst pellet surfaces.
Reaction rate (rA′)depends on catalyst mass (W), not reactor volume (V).
Typical examples: Catalytic converters, petroleum refining, air purification

Mole balance: PBR
Assumptions

- Steady-State Operation
- One-Dimensional Flow
- No pressure drop; Constant Physical Properties
- No Back-Mixing: The reactor operates under plug flow conditions with no back-mixing or axial dispersion of reactants or products.
- Constant Cross-Sectional Area: The cross-sectional area of the PFR is constant along its length.
- Uniform Packing: Constant surface area for reaction per unit reactor volume.
Mole balance: PBR

Selection of reactors
- Batch
- small scale, production of expensive products (e.g. pharmacy)
- high labor costs per batch
- difficult for large-scale production
- CSTR: most homogeneous liquid-phase flow reactors
- when intense agitation is required
- relatively easy to maintain good temperature control
- the conversion of reactant per volume of reactor is the smallest of the flow reactors - very large reactors are necessary to obtain high conversions
- PFR: most homogeneous gas-phase flow reactors
- relatively easy to maintain
- usually produces the highest conversion per reactor volume (weight of catalyst if it is a packed-bed catalyze gas reaction) of any of the flow reactors
- difficult to control temperature within the reactor
- hot spots can occur
This component is an instance of the CodeMirror interactive text editor. The editor has been configured so that the Tab key controls the indentation of code. To move focus away from the editor, press the Escape key, and then press the Tab key directly after it. Escape and then Shift-Tab can also be used to move focus backwards.

Chemical Reaction Engineering